
169 Bài tập Hàm số từ đề thi Đại học có lời giải chi tiết
Trắc Nghiệm Tổng Hợp Toán 12 (Có Đáp Án) <br> Lớp 12;Toán <br>
Số câu hỏi: 164 câuSố mã đề: 6 đềThời gian: 1 giờ
163,950 lượt xem 12,607 lượt làm bài
Xem trước nội dung:
Tìm tất cả giá trị thực của tham số m để mọi tiếp tuyến của đồ thị hàm số có hệ số góc luôn dương.
Đường cong ở hình bên là đồ thị của hàm số nào sau đây?
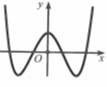
Hàm số đồng biến trên khoảng
Tìm điều kiện của tham số thực m để hàm số có 3 cực trị.
Điểm cực tiểu của đồ thị hàm số là
Cho hàm số với . Mệnh đề nào sau đây là mệnh đề đúng
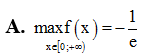
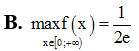
Đồ thị hàm số có bao nhiêu đường tiệm cận đứng
Đồ thị như hình vẽ là của hàm số nào trong các hàm số đã cho dưới đây
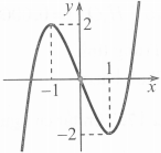
Cho đồ thị hàm số y=f(x) như hình vẽ. Tìm tất cả các giá trị thực m để phương trình f(x) +1=m có ba nghiệm phân biệt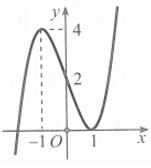
Cho hàm số Khi đó giá trị của f(1) bằng bao nhiêu
Tìm tất cả các giá trị thực của tham số m để hàm số nghịch biến trên khoảng (-3;1)
Cho hàm số y = f(x) có bảng biến thiên như sau:
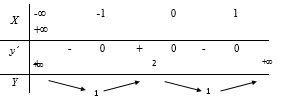
Mệnh đề nào dưới đây đúng?
Tìm giá trị lớn nhất M của hàm số
Đường cong ở hình bên là đồ thị của hàm số nào dưới đây?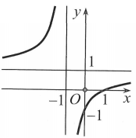
Cho hàm số y = f(x) có bảng biến thiên như sau:
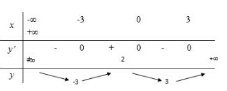
Tìm tất cả giá trị thực của tham số m để phương trình f(x) - m - 0 có bốn nghiệm phân biệt.
Cho hàm số (m là tham số thức) thỏa mãn . Giá trị m thuộc tập nào dưới đây?
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số cắt trục hoành tại một điểm duy nhất
Hàm số nào dưới đây đồng biến trên khoảng .
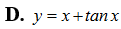
Cho hàm số với m là tham số thực. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m trong khoảng (-50;50) để hàm số nghịch biến trên (-1;1). Số phần tử của S là:
Cho hàm số f(x) xác định, liên tục trên R và có bảng biến thiên như sau: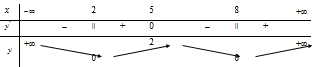
Mệnh đề nào dưới đây đúng?
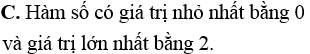
Cho hàm số . Mệnh đề nào sau đây đúng?
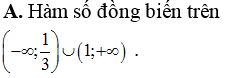
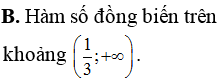
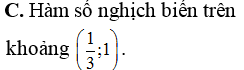
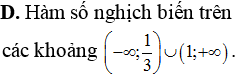
Gọi S là tập hợp tất cả các giá trị nguyên dương và nhỏ hơn 2018 của tham số m để hàm số nghịch biến trên khoảng (1;9). Tính số phần tử của tập hợp S.
Gọi M, N lần lượt là GTLN, TNNN của hàm số trên [1;2]. Khi đó tổng M+N bằng
Tìm tổng tất cả các giá trị thực của tham số m sao cho đường thẳng đi qua hai điểm cực trị của đồ thị hàm số song song đường thẳng y= -4x.
Tính tổng S tất cả các giá trị nguyên dương m sao cho đồ thị hàm số có 2 tiệm cận ngang.
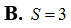
Đề thi tương tự
1 mã đề 40 câu hỏi 50 phút
2,311 xem169 thi
