261 Bài tập trắc nghiệm Hình học Mặt nón, mặt trụ, mặt cầu cực hay có lời giải chi tiết

Trong các khối trụ tròn có tổng độ dài đường sinh và bán kính đường tròn đáy bằng 6cm thì khối trụ có thể tích lớn nhất có đường sinh h bằng bao nhiêu?

Tính diện tích S của mặt cầu ngoại tiếp tứ diện AB’C’D’ biết ABCDA’B’C’D’ là hình lập phương cạnh a

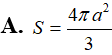
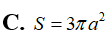
Mộp mp (P) chứa trục của 1 hình trụ tròn cắt hình trụ đó theo thiết diện là 1 hình vuông cạnh a. Tính thể tích V của hình trụ đó.

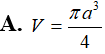
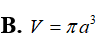
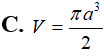
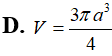
Một hình nón tròn xoay có thể tích $V=\frac{{\mathrm{\pi a}}^3}{9}$ và góc ở đỉnh hình nón bằng ${60}^o$. Tính diện tích xung quanh $\left(S_{xq}\right)$của hình nón đó

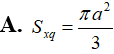
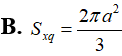
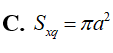
Cho I(2; -4; 1). Xác định bán kính R của mặt cầu (S) tâm I, cắt trục Oy tại A, B sao cho AB = 4

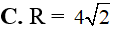
Có bao nhiêu mặt cầu tiếp xúc với cả 3 mặt phẳng tọa độ và có tâm thuộc mặt phẳng  $\left(P\right): x+y-6=0$

Hình nón tròn xoay nội tiếp trong mặt cầu bán kính  $R=\frac{3}{4}$ có thể tích lớn nhất bằng bao nhiêu  $\left(V_{max}\right)$

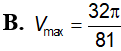
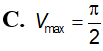
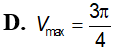
Hình chóp SABCD có đáy ABCD là hình chữ nhật. $SA\perp \left(ABCD\right)$ Biết $SA=a, BC=a\sqrt{3}, CD=2a$. Tính bán kính R của mặt cầu ngoại tiếp SABCD

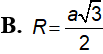
$△ABC$ cân tại A, AB = a, $\widehat{ABC}={120}^o$. Cho $△ABC$ quay quanh BA tạo thành một khối tròn xoay có thể tích V. Tính V

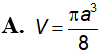
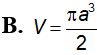
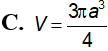
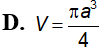
Khối trụ tròn nội tiếp trong mặt cầu bán kính R có diện tích xung quanh (S_xq) lớn nhất bằng bao nhiêu?

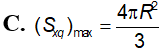
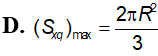
Một khối trụ tròn có 1 đường tròn đáy thuộc mặt bên của 1 hình nón xoay, đáy còn lại thuộc mặt đáy hình nón. Biết chiều cao hình trụ bằng nửa chiều cao hình nón. Tính tỷ số $k=\frac{V_1}{V_2}$ với $V_{{}^1},V_2$ tương ứng là thể tích hình trụ và hình nón.

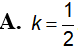
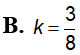
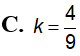
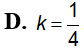
$△$vuông ABC (tại A) có AB=4a, AC=3a quay quanh BC tạo thành khối tròn xoay có thể tích V. Tính V

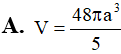
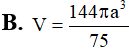
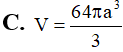
Hình nón nội tiếp trong mặt cầu bán kính R. Biết góc ở đỉnh hình nón bằng 120⁰. Tính thể tích V của hình nón theo R

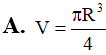
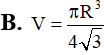
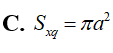
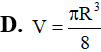
$△$ABC vuông tại A. M là trung điểm cạnh huyền BC. Hạ $MH\perp AB,MK\perp AC$ Cho $△$ABC và hình chữ nhật AHMK quay quanh AB tạo thành các khối tròn xoay có thể tích V₁, V₂. Tính $k=\frac{V_2}{V_1}$

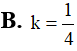
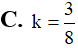
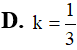
Cho tam giác ABC vuông tại A, $\widehat{ABC}={60}^o$. Cho tam giác ABC lần lượt quay quanh AB; AC tạo thành các khối tròn xoay tương ứng có thể tích $V_1,V_2$. Tính $k=\frac{V_1}{V_2}$

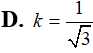
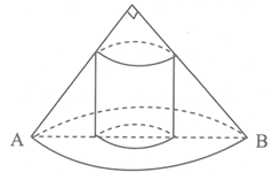
Xét các hình trụ tròn nội tiếp trong một hình nón (theo hình vẽ) biết góc ở đỉnh hình nón bằng ${90}^o,AB=2a$. Khi đó thể tích hình trụ lớn nhất $\left(V_{max}\right)$ bằng bao nhiêu?

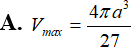
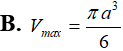
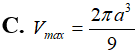
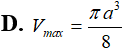
Trong bốn hình sau: hình trụ tròn, hình cầu, hình hộp ABCDA'B'C'D' và tứ diện đều ABCD có bao nhiêu hình có tâm đối xứng?

Tính diện tích xung quanh (S) của hình nón nội tiếp một mặt cầu bán kính R (nghĩa là đỉnh và đường tròn đáy hình nón đều thuộc mặt cầu), biết góc ở đỉnh hình nón bằng  ${90}^o$

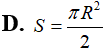
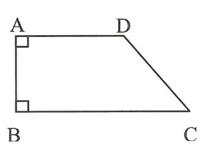
Cho hình thang vuông ABCD (như hình vẽ) có AB=a, BC=4a, $CD=a\sqrt{5}$. Cho ABCD quay quanh BC tạo thành khối tròn xoay có thể tích V. Tính V.

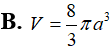
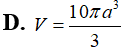
Mặt cầu (S) tâm I(2;-3;1) tiếp xúc với mặt phẳng Oxy có bán kính R bằng:

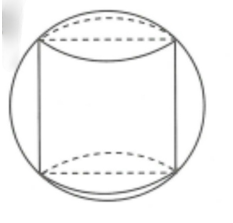
Một khối trụ tròn nội tiếp trong một mặt cầu (Hình vẽ), biết chiều cao hình trụ bằng bán kính mặt cầu, tính tỉ số $k=\frac{V_1}{V_2}$ với $V_1,V_2$lần lượt là thể tích khối trụ và mặt cầu

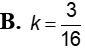
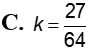
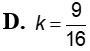
Tìm bán kính mặt cầu ngoại tiếp tứ diện ABCD với A(3;3;0); B(3;0;3); C(0;3;3) và D(3;3;3)

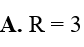
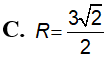
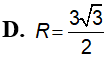
Hình trụ nội tiếp trong một mặt cầu được cắt bởi một thiết diện chứa trục hình trụ đó tạo thành thiết diện là một hình vuông. Tính $k=\frac{V_T}{V_C}$ (V_T, V_C lần lượt là thể tích hình trụ, hình cầu).

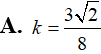
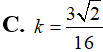
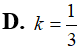
Biết diện tích xung quanh của một hình nón gấp đôi diện tích đáy của hình nón đó. Xác định góc ở đỉnh hình nón đó.

Hình chóp S.ABC có SA ^ (ABC), DABC vuông tại C có SA = 2a, AC = a, BC = a $\sqrt{3}$. Tính bán kính R của mặt cầu ngoại tiếp SABC.

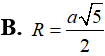
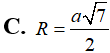
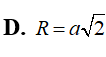
Mặt cầu (S): x² + y² + 2mx - 2my + z² = m² - 6m + 10 có bán kính nhỏ nhất (R_min) bằng bao nhiêu?

$△$ABC vuông tại A có AC=a, $\widehat{ABC}={30}^0$ Điểm M di động trên BC, hạ $MH\perp AC,MK\perp AB$ Xét các hình trụ tròn sinh ra bởi MHAK quay quanh AB. Tìm GTLN (V_max) của hình trụ đó:

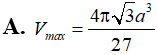
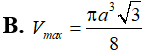
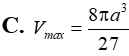
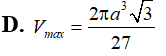
Vẫn với hình chóp ở câu 34. Tính bán kính R của mặt cầu ngoại tiếp hình chóp

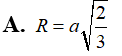
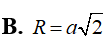
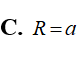
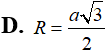
Hình nón tròn xoay nội tiếp trong mặt cầu bán kính R với chiều cao hình nón bằng $\frac{3R}{2}$. Tính thể tích V của hình nón.

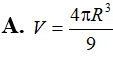
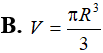
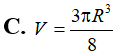
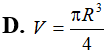
$△$ABC vuông tại A có $AB=a\sqrt{3}, AC=a$ Cho DABC quay quanh BC tạo thành khối tròn xoay có thể tích V. Tính V