
Ôn thi Cấp tốc 789+ vào 10 môn Toán khu vực Bắc Ninh 2024 - 2025 (Đề 20)
Đề chính thức
Lớp 9;Toán
Thời gian làm bài: 1 giờ
Hãy bắt đầu chinh phục nào!
Xem trước nội dung:
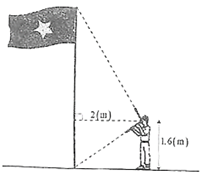
Một học sinh cầm thước êke đưng cách cột cờ 2 m . Bạn ấy lần lượt nhìn theo hai cạnh góc vuông của êke thì thấy ngọn và chân của cột cờ (tham khảo hình vẽ). Biết mắt học sinh cách mặt đất \(1,6\;{\rm{m}}\). Khi đó, chiều cao của cột cờ bằng
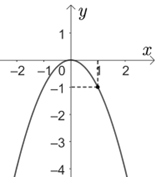
Hình vẽ dưới đây là của đồ thị hàm số nào?
Rút gọn biểu thức \(B = \left( {\frac{1}{{\sqrt x - 1}} - \frac{1}{{\sqrt x + 1}}} \right):\frac{{x + 1}}{{x - 1}}\) với \(x \ge 0\,;\,\,x e 1.\)
Cho phương trình \({x^2} - 2x + m - 1 = 0\,\,\,\left( 1 \right)\) (ẩn \(x\), tham số \(m\)).
1) Giải phương trình \(\left( 1 \right)\) với \(m = - 2\).
2) Tìm \(m\) để phương trình \(\left( 1 \right)\) có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) thỏa mãn \({x_1} + 2{x_2} = 0\).
Một đội xe vận tải được phân công chở hết 171 tấn hàng. Trước giờ khởi hành có 1 xe phải đi làm nhiệm vụ khác. Để chở hết số hàng trên mỗi xe còn lại phải chờ thêm 0,5 tấn hàng so với dự định. Tính số xe ban đầu của đội xe, biết rằng mỗi xe đều chở khối lượng hàng như nhau.
Cho đường tròn \(\left( {O\,;R} \right)\) có đường kính \[MN.\] Gọi đường thẳng \(d\) là tiếp tuyến của đường tròn \[\left( O \right)\] tại điểm \(N\). Lấy điểm \(E\) di động trên đường tròn \[\left( O \right)\]\((E\) không trùng với \(M\) và \(N),\) tia \[ME\] cắt đường thẳng \(d\) tại điểm \(F.\) Kẻ \[OP\] vuông góc với \[ME\] tại điểm \(P\), tia \[PO\] cắt đường thẳng \(d\) tại điểm \(Q\), tia \[FO\] cắt \[MQ\] tại điểm \(D.\)
1) Chứng minh tứ giác \[ONFP\] nội tiếp đường tròn.
2) Chứng minh \(MD \cdot DQ = DO \cdot DF.\)
3) Tìm được bao nhiêu điểm \[E\] trên đường tròn \[\left( O \right)\] để tổng \(MF + 4ME\) đạt giá trị nhỏ nhất?
Cho ba số thực dương \[a,{\rm{ }}b,\,\,c\] thỏa mãn \(\frac{1}{{1 + a}} + \frac{{25}}{{25 + 2b}} \le \frac{{4c}}{{4c + 81}}\).
Tìm giá trị nhỏ nhất của biểu thức \(P = a \cdot b \cdot c.\)
Xem thêm đề thi tương tự

Đề chính thức
Lớp 9;Toán
5 câu hỏi 1 mã đề 1 giờ
160,744 lượt xem 86,548 lượt làm bài

Đề chính thức
Lớp 9;Toán
13 câu hỏi 1 mã đề 1 giờ
188,410 lượt xem 101,444 lượt làm bài

Đề chính thức
Lớp 9;Toán
8 câu hỏi 1 mã đề 1 giờ
164,839 lượt xem 88,753 lượt làm bài

Đề chính thức
Lớp 9;Toán
10 câu hỏi 1 mã đề 1 giờ
188,797 lượt xem 101,654 lượt làm bài

Đề chính thức
Lớp 9;Toán
5 câu hỏi 1 mã đề 1 giờ
172,538 lượt xem 92,897 lượt làm bài

Đề chính thức
Lớp 9;Toán
5 câu hỏi 1 mã đề 1 giờ
179,634 lượt xem 96,719 lượt làm bài

Đề chính thức
Lớp 9;Toán
5 câu hỏi 1 mã đề 1 giờ
167,192 lượt xem 90,020 lượt làm bài

Đề chính thức
Lớp 9;Toán
5 câu hỏi 1 mã đề 1 giờ
160,939 lượt xem 86,653 lượt làm bài

Đề chính thức
Lớp 9;Toán
5 câu hỏi 1 mã đề 1 giờ
172,568 lượt xem 92,911 lượt làm bài
