Trang chủ Đề thi Lớp 8 Toán 13132
thumbnail

Trắc nghiệm chuyên đề Toán 8 Chủ đề 13: Ôn tập và kiểm tra có đáp án

Chuyên đề Toán 8
Chuyên đề 5: Tứ giác
Lớp 8;Toán

Đề thi nằm trong bộ sưu tập: Tuyển tập đề thi trắc nghiệm ôn luyện Toán 8

Số câu hỏi: 99 câuSố mã đề: 3 đềThời gian: 1 giờ

170,774 lượt xem 13,132 lượt làm bài


Chọn mã đề:


Bạn chưa làm Đề số 1!!!

 

Xem trước nội dung:

Câu 1: 1 điểm
Cho tứ giác ABCD, trong đó  A ^ + B ^ = 1400. Tổng  C ^ + D ^ = ?
A.  
 2200
B.  
 2000
C.  
 1600
D.  
 1500
Câu 2: 1 điểm
Số đo các góc của tứ giác ABCD theo tỷ lệ A:B:C:D = 4:3:2:1. Số đo các góc theo thứ tự đó là?
A.  
 1200;900;600;300.
B.  
 1400;1050;700;350.
C.  
 1440;1080;720;360.
D.  
 Cả A, B, C đều sai.
Câu 3: 1 điểm
Chọn câu đúng trong các câu sau:
A.  
 Tứ giác ABCD có 4 góc đều nhọn.
B.  
 Tứ giác ABCD có 4 góc đều tù.
C.  
 Tứ giác ABCD có 2 góc vuông và 2 góc tù.
D.  
 Tứ giác ABCD có 4 góc đều vuông.
Câu 4: 1 điểm
Cho tứ giác ABCD có  A ^ = 650;  B ^ = 1170;  C ^ = 710. Số đo góc  D ^ = ?
A.  
 1190.
B.  
 1070.
C.  
 630.
D.  
 1260.
Câu 5: 1 điểm
Cho tứ giác ABCD trong đó có  B ^ = 750;  D ^ = 1200. Khi đó  A ^ + C ^ = ?
A.  
 1900
B.  
 1300
C.  
 2150
D.  
 1650
Câu 6: 1 điểm
Chọn câu đúng trong các câu sau:
A.  
 Hình thang có ba góc tù, một góc nhọn.
B.  
 Hình thang có ba góc vuông, một góc nhọn.
C.  
 Hình thang có ba góc nhọn, một góc tù.
D.  
 Hình thanh có nhiều nhất hai góc nhọn và nhiều nhất hai góc tù.
Câu 7: 1 điểm
Một hình thang có một cặp góc đối là 1250 và 750, cặp góc đối còn lại của hình thang đó là ?
A.  
 1050, 550
B.  
 1050, 450
C.  
 1150, 550
D.  
 1150, 650
Câu 8: 1 điểm
Hình thang ABCD có  C ^ + D ^ = 1500. Khi đó  A ^ + B ^ = ?
A.  
 2200
B.  
 2100
C.  
 2000
D.  
 1900
Câu 9: 1 điểm
Cho hình thang ABCD trong đó có  A ^ = 1200, B ^ = 600, D ^ = 1350 thì số đo của góc  C ^ = ?
A.  
 550
B.  
 450
C.  
 500
D.  
 600
Câu 1: 1 điểm

Điền cụm từ thích hợp vào chỗ trống

Hình thang cân là…………………………………..

Câu 2: 1 điểm
Hình thang có………………. là hình thang cân .
Câu 3: 1 điểm

Hai cạnh bên của hình thang cân…………………..

Câu 4: 1 điểm

Hình thang cân có hai góc kề một đáy…………….

Câu 5: 1 điểm

Điền chữ “Đ” hoặc “S” vào mỗi câu khẳng định sau:

A. Tứ giác có hai cạnh bên bằng nhau là hình thang cân.

Câu 6: 1 điểm

B. Hình thang cân có hai cạnh bên bằng nhau.

Câu 7: 1 điểm

C. Hình thang cân có hai góc kề một cạnh đáy bù nhau.

Câu 8: 1 điểm

D. Hình thang cân có hai góc kề một cạnh đáy bằng nhau.

Câu 10: 1 điểm
Cho hình thang cân ABCD (như hình vẽ) có  B A D ^ = 600. Số đo của  B C D ^ = ?
A.  
 500
B.  
 600
C.  
 1200
D.  
 800
Câu 11: 1 điểm
Cho tam giác ABC có D, E lần lượt là trung điểm của AB, AC. Phát biểu nào sau đây sai?
A.  
 DE là đường trung bình của tam giác ABC.
B.  
 DE song song với BC.
C.  
 DECB là hình thang cân.
D.  
 DE có độ dài bằng nửa BC.
Câu 12: 1 điểm
Cho tam giác ABC có D, E lần lượt là trung điểm của AB, AC và DE = 4cm. Biết đường cao AH = 6cm. Diện tích của tam giác ABC là?
A.  
 S = 24( cm2 )
B.  
 S = 16( cm2 )
C.  
 S = 48( cm2 )
D.  
 S = 32( cm2 )
Câu 13: 1 điểm
Chọn phát biểu đúng
A.  
 Đường trung bình của hình thang là đoạn thẳng nối hai trung điểm của hai cạnh bên của hình thoi.
B.  
 Đường trung bình của hình thang là đoạn thẳng nối hai trung điểm của hai cạnh đối của hình thoi.
C.  
 Đường trung bình của hình thang thì song song với hai đáy và bằng tổng hai hai đáy.
D.  
 Một hình thang có thể có một hoặc nhiều đường trung bình.
Câu 14: 1 điểm
Với a, b, h lần lượt là độ dài đáy lớn, đáy nhỏ và chiều cao của hình thang thì công thức diện tích của hình thang là ?
A.  
 S = ( a + b )h
B.  

 S = 1 2 ( a + b )h

C.  

 S = 1 3 ( a + b )h

D.  

 S = 1 4 ( a + b )h

Câu 15: 1 điểm
Chọn phương án đúng nhất trong các phương án sau
A.  
 Đường thẳng đi qua hai đáy của hình thang là trục đối xứng của hình thang đó.
B.  
 Đương thẳng đi qua hai đáy của hình thang cân là trục đối xứng của hình thang cân.
C.  
 Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang cân đó.
D.  
 Cả A, B, C đều sai.
Câu 16: 1 điểm
Cho đoạn thẳng AB có độ dài là 3cm và đường thẳng d, đoạn thẳng A'B' đối xứng với AB qua d, khi đó độ dài của A'B' là ?
A.  
 3cm
B.  
 6cm
C.  
 9cm
D.  
 12cm
Câu 17: 1 điểm
Tam giác ABC đối xứng với tam giác A'B'C' qua đường thẳng d, biết chu vi của tam giác ABC là 48cm thì chu vi của tam giác A'B'C' là ?
A.  
 24cm
B.  
 32cm
C.  
 40cm
D.  
 48cm
Câu 18: 1 điểm
Chọn phương án sai trong các phương án sau?
A.  
 Tứ giác có các cạnh đối song song là hình bình hành.
B.  
 Tứ giác có các cạnh đối bằng nhau là hình bình hành.
C.  
 Tứ giác có hai góc đối bằng nhau là hình bình hành.
D.  
 Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
Câu 19: 1 điểm
Chọn phương án đúng trong các phương án sau.
A.  
 Hình bình hành là tứ giác có hai cạnh đối song song.
B.  
 Hình bình hành là tứ giác có các góc bằng nhau.
C.  
 Hình bình hành là tứ giác có các cạnh đối song song.
D.  
 Hình bình hành là hình thang có hai cạnh kề bằng nhau.
Câu 20: 1 điểm
Cho hình bình hành ABCD có  A ^ = 1200, các góc còn lại của hình bình hành là?
A.  

  B ^ = 600,  C ^ = 1200,  D ^ = 600.

B.  

  B ^ = 1100,  C ^ = 800,  D ^ = 600.

C.  

  B ^   = 800,  C ^   = 1200,  D ^ = 800.

D.  

  B ^   = 1200,  C ^ = 600,  D ^ = 1200.

Câu 21: 1 điểm
Cho hình bình hành ABCD có A ^ - B ^ = 200. Xác định số đo góc A và B?
A.  
A ^ = 800, B ^ = 1000
B.  
A ^ = 1000, B ^ = 800
C.  
A ^   = 800, B ^ = 600
D.  
A ^ = 1200, B ^ = 1000
Câu 22: 1 điểm
Cho hình bình hành ABCD, có I là giao điểm của AC và BD. Chọn phương án đúng trong các phương án sau
A.  
AC = BD
B.  
Δ ABD cân tại
C.  
BI là đường trung tuyến của Δ ABC
D.  
A ^ + B ^ = C ^ + D ^ .
Câu 23: 1 điểm
Chọn đáp án đúng trong các đáp án sau
A.  
 Hai điểm được gọi là đối xứng với nhau qua điểm O nếu O thuộc đoạn nói hai điểm đó.
B.  
 Hai điểm được gọi là đối xứng với nhau qua điểm O nếu O các đều hai điểm đó
C.  
 Hai điểm được gọi là đối xứng với nhau qua điểm O nếu O là trung điểm của đoạn thẳng nối hai điểm đó.
D.  
 Hai điểm được gọi là đối xứng với nhau qua điểm O nếu O là đoạn thẳng trung trực của hai điểm đó.
Câu 24: 1 điểm
Cho AB = 6cm, A' là điểm đối xứng với A qua B, AA' có độ dài bằng bao nhiêu ?
A.  
 AA' = 3cm
B.  
 AA' = 12cm
C.  
 AA' = 6cm
D.  
 AA' = 9cm
Câu 25: 1 điểm
Chọn phương án sai trong các phương án sau đây
A.  
 Hai đoạn thẳng đối xứng với nhau qua một điểm thì chúng bằng nhau.
B.  
 Hai góc đối xứng với nhau qua một điểm thì chúng bằng nhau.
C.  
 Hai đường thẳng đối xứng với nhau qua một điểm thì chúng bằng nhau.
D.  
 Hai tam giác đối xứng với nhau qua một điểm thì chúng bằng nhau.
Câu 26: 1 điểm
Hình nào dưới đây có tâm không phải là giao điểm của hai đường chéo?
A.  
 Hình bình hành
B.  
 Hình chữ nhật
C.  
 Hình thoi
D.  
 Hình thang
Câu 27: 1 điểm
Cho tam giác ABC và tam giác A'B'C' đối xứng với nhau qua điểm I biết AB = 4cm, AC = 8cm và chu vi của tam giác ABC bằng 22cm. Hỏi độ dài cạnh B'C' của tam giác A'B'C' là?
A.  
 B'C' = 9cm
B.  
 B'C' = 8cm
C.  
 B'C' = 4cm
D.  
 B'C' = 10cm
Câu 28: 1 điểm
Chọn đáp án đúng nhất trong các đáp án sau?
A.  
 Hình chữ nhật là tứ giác có bốn cạnh bằng nhau.
B.  
 Hình chữ nhật là tứ giác có bốn góc vuông.
C.  
 Hình chữ nhật là tứ giác có hai góc vuông.
D.  
 Các phương án trên đều không đúng.
Câu 29: 1 điểm
Tìm câu sai trong các câu sau
A.  
 Trong hình chữ nhật có hai đường chéo bằng nhau.
B.  
 Trong hình chữ nhật có hai đường chéo cắt nhau tại trung điểm mỗi đường.
C.  
 Trong hình chữ nhật có hai cạnh kề bằng nhau.
D.  
 Trong hình chữ nhật, giao của hai đường chéo là tâm của hình chữ nhật đó
Câu 30: 1 điểm
Các dấu hiệu nhận biết sau, dấu hiệu nào nhận biết chưa đúng?
A.  
 Hình bình hành có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình chữ nhật.
B.  
 Tứ giác có ba góc vuông là hình chữ nhật.
C.  
 Hình thang cân có một góc vuông là hình chữ nhật.
D.  
 Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.
Câu 31: 1 điểm
Khoanh tròn vào phương án sai
A.  
 Trong tam giác vuông đường trung tuyến ứng với cạnh huyền và bằng nửa cạnh huyền.
B.  
 Trong tam giác, đường trung tuyến với với một cạnh và bằng nửa cạnh ấy thì tam giác đó là tam giác vuông.
C.  
 Trong tam giác vuông, đường trung tuyến ứng với cạnh góc vuông không bằng cạnh ấy.
D.  
 Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền thì vuông góc với cạnh huyền.
Câu 32: 1 điểm
Trong hình chữ nhật có kích thước lần lượt là 5cm và 12cm. Độ dài đường chéo của hình chữ nhật là ?
A.  
 17cm
B.  
 13cm
C.  

119 cm

D.  
 12cm
Câu 33: 1 điểm
Chọn phương án đúng nhất trong các phương án sau?
A.  
 Khoảng cách giữa hai đường thẳng song song là khoảng cách từ một điểm tùy ý trên đường thẳng này đến một điểm tùy ý trên đường thẳng kia.
B.  
 Khoảng cách giữa hai đường thẳng song song là độ dài từ một điểm tùy ý trên đường thẳng này đến một điểm tùy ý trên đường thẳng kia.
C.  
 Khoảng cách giữa hai đường thẳng song song là khoảng cách từ một điểm tùy ý trên đường thẳng này đến đường thẳng kia
D.  
 Các ba đáp án trên đều sai.
Câu 34: 1 điểm
Chọn phương án đúng trong các phương án sau
A.  
 Các điểm cách đường thẳng b một khoảng cho trước bằng h nằm trên một đường thẳng song song với b và cách b một khoảng bằng h.
B.  
Các điểm cách đường thẳng b một khoảng cho trước bằng h nằm trên hai đường thẳng song song với b và cách b một khoảng bằng h.
C.  
 Các điểm cách đường thẳng b một khoảng cho trước bằng h nằm trên ba đường thẳng song song với b và cách b một khoảng bằng h
D.  
 Cả ba đáp án đều sai.
Câu 35: 1 điểm

Cho hình sau trong đó các đường thẳng a,b,c,d song song với nhau. Nếu các đường thẳng a,b,c,d song song cách đều thì :

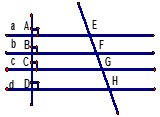
Hình ảnh
A.  
 EF > FG > GH
B.  
 EF < FG < GH
C.  
 EF = FG = GH
D.  
 Cả 3 đáp án đều sai
Câu 36: 1 điểm
Khoanh tròn vào phương án đúng trong các phương án sau ?
A.  
 Hình thoi là tứ giác có bốn góc bằng nhau.
B.  
 Hình thoi là tứ giác có hai cạnh đối bằng nhau.
C.  
 Hình thoi là tứ giác có ba góc vuông.
D.  
 Hình thoi là tứ giác có bốn cạnh bằng nhau.
Câu 37: 1 điểm
Trong các khẳng định sau, khẳng định nào sai về hình thoi ?
A.  
 Hai đường chéo bằng nhau.
B.  
 Hai đường chéo vông góc và là các đường phân giác của các góc hình thoi.
C.  
 Hai đường chéo cắt nhau tại trung điểm mỗi đường.
D.  
 Hình thoi có 4 cạnh bằng nhau.
Câu 38: 1 điểm
Hai đường chéo của hình thoi có độ dài lần lượt là 8cm và 10cm. Độ dài cạnh của hình thoi đó là?
A.  
 6cm.
B.  

  41 cm.

C.  

  164 cm.

D.  
 9cm.
Câu 39: 1 điểm
Hình thoi có độ dài các cạnh là 4cm thì chu vi của hình thoi là ?
A.  
 8cm.
B.  
 44cm.
C.  
 16cm.
D.  
 Cả A, B, C đều sai.
Câu 40: 1 điểm
Các phương án sau, phương án nào sai?
A.  
 Các trung điểm của bốn cạnh hình chữ nhật là các đỉnh của một hình thoi.
B.  
 Các trung điểm của bốn cạnh hình thoi là bốn đỉnh của hình chữ nhật.
C.  
 Giao điểm của hai đường chéo của hình thoi là tâm đối xứng của hình thoi đó.
D.  
 Hình thoi của bốn trục đối xứng.
Câu 41: 1 điểm
Hãy khoan tròn vào phương án đúng nhất trong các phương án sau ?
A.  
 Hình vuông là tứ giác có 4 góc vuông và 4 cạnh bằng nhau.
B.  
 Hình vuông là tứ giác có 4 góc bằng nhau.
C.  
 Hình vuông là tứ giác có 4 cạnh bằng nhau.
D.  
 Hình vuông là tứ giác có hai cạnh kề bằng nhau.
Câu 42: 1 điểm
Hãy chọn đáp án sai trong các phương án sau đây ?
A.  
 Trong hình vuông có hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường.
B.  
 Trong hình vuông có hai đường chéo không vuông góc với nhau.
C.  
 Trong hình vuông thì hai đường chéo đồng thời là hai trục đối xứng của hình vuông.
D.  
 Trong hình vuông có hai đường chéo vuông góc với nhau và bằng nhau.
Câu 43: 1 điểm
Trong các dấu hiệu nhận biết sau thì dấu hiệu nào không đủ điều kiện để tứ giác là hình vuông?
A.  
 Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
B.  
 Hình chữ nhật có hai đường chéo vuông gócvới nhau là hình vuông.
C.  
 Hình chữ nhật có một đường chéo là đường phân giác của một góc là hình vuông.
D.  
 Hình bình hành có hai đường chéo bằng nhau là hình vuông.
Câu 44: 1 điểm
Tìm câu nói đúng khi nói về hình vuông?
A.  
 Hình vuông vừa là hình chữ nhật, vừa là hình thoi.
B.  
 Hình thoi có một góc vuông là hình vuông.
C.  
 Hình thoi có hai đường chéo bằng nhau là hình vuông.
D.  
 Các phương án đều đúng.
Câu 45: 1 điểm
Một hình vuông có độ dài cạnh bằng 4cm thì độ dài đường chéo của hình vuông là ?
A.  
 8cm
B.  

  32 cm

C.  
 5cm
D.  
 4cm
Câu 9: 1 điểm
Cho tứ giác ABCD trong đó A ^ = 730, B ^ = 1120, D ^ = 840. Tính số đo góc  C ^ ?
Câu 10: 1 điểm
Cho tứ giác ABCD có  A ^ = 700, B ^ = 900. Các tia phân giác của các góc C và D cắt nhau tại O. Tính số đo góc CODˆ ?
Câu 11: 1 điểm
Hình thang vuông ABCD có  A ^ = D ^ = 900; AB = AD = 3cm;CD = 6cm. Tính số đo góc B và C của hình thang ?
Câu 12: 1 điểm
Tính các góc của hình thang cân, biết có một góc bằng 600
Câu 13: 1 điểm
Cho tam giác ABC( AB > AC ) có  A ^ = 500. Trên cạnh AB lấy điểm D sao cho BD = AC. Gọi E,F lần lượt là trung điểm của cạnh AD, BC. Tính B E F ^ = ?
Câu 14: 1 điểm

Tìm giá trị của x từ các thông tin trên hình sau ?

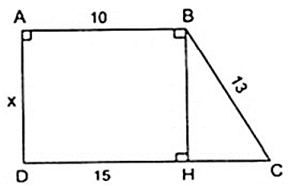
Hình ảnh
Câu 15: 1 điểm

Chứng minh rằng các đường cao của hình thoi bằng nhau.

Câu 16: 1 điểm
Cho hình thang ABCD ( AB//CD ) có AB = 2cm, CD = 5cm, AD = 7cm. Gọi E là trung điểm của BC. Tính A E D ^ = ?
Câu 17: 1 điểm

Cho Δ ABC có  A ^ = 500, điểm M thuộc cạnh BC. Vẽ điểm D đối xứng với M qua AB, vẽ điểm E đối xứng với M qua AC.

a) Chứng minh rằng AD = AE.

Câu 18: 1 điểm
b) Tính số đo góc  D A E ^ = ?
Câu 19: 1 điểm
Cho tam giác nhọn ABC, các đường cao BD, CE. Gọi H, K lần lượt là các chân đường cao kẻ từ kẻ từ B và C đến đường thẳng DE. Chứng minh rằng HE = DK.
Câu 20: 1 điểm

Cho hình vuông ABCD cạnh bằng a. Trên hai cạnh BC, CD lấy lần lượt hai điểm M, N sao cho  M A N ^ = 450. Trên tia đối của của tia DC lấy điểm K sao cho DK = BM. Hãy tính :

a) Tính số đo  K A N ^ = ?

Câu 21: 1 điểm
b) Chu vi tam giác MCN theo a.
Câu 22: 1 điểm

Tính chiều cao của hình thang cân ABCD, biết rằng cạnh bên AD = 5cm, cạnh đáy AB = 6cm và CD = 14cm.

Câu 23: 1 điểm

Tính chiều cao BH của hình thang cân ABCD, biết AC ⊥ BD và hai cạnh đáy AB = a, CD = b. Từ đó suy ra cách vẽ hình.

Câu 24: 1 điểm

Cho hình vuông ABCD. Gọi I,K lần lượt là trung điểm của AD và DC.

a) Chứng minh rằng BI ⊥ AK.

Câu 25: 1 điểm
b) Gọi E là giao điểm của BI và AK. Chứng minh rằng CE = AB.
Câu 26: 1 điểm

Cho hai điểm A, B cùng nằm trên một nửa mặt phẳng có bờ là đường thẳng d. Tìm trên d điểm M sao cho tổng MA + MB nhỏ nhất.

Câu 27: 1 điểm

Cho hình thang vuông ABCD có  A ^ = D ^ = 900 và CD = 2AB. Kẻ DE ⊥ AC, gọi I là trung điểm của EC. Chứng minh rằng  B I D ^ = 900.

Câu 28: 1 điểm

Cho hình vuông ABCD. Trên cạnh BC lấy điểm M, qua A kẻ AN ⊥ AM (điểm N thuộc tia đối của tia DC). Gọi I là trung điểm của MN. Chứng minh rằng:

a) AM = AN

Câu 29: 1 điểm
b) Ba điểm B, I, D thẳng hàng.

Đề thi tương tự

Trắc nghiệm chuyên đề Toán 8 Chủ đề 3: Phương trình đưa được về dạng ax + b = 0 có đáp ánLớp 8Toán

1 mã đề 18 câu hỏi 1 giờ

177,51013,649

Trắc nghiệm chuyên đề Toán 8 Chủ đề 4. Quy đồng mẫu thức nhiều phân thức có đáp ánLớp 8Toán

1 mã đề 6 câu hỏi 1 giờ

173,73413,359

Trắc nghiệm chuyên đề Toán 8 Chủ đề 4. Diện tích hình thang có đáp ánLớp 8Toán

1 mã đề 6 câu hỏi 1 giờ

152,02111,689

Trắc nghiệm chuyên đề Toán 8 Chủ đề 12: Hình vuông có đáp ánLớp 8Toán

1 mã đề 10 câu hỏi 1 giờ

175,60613,503

Trắc nghiệm chuyên đề Toán 8 Chủ đề 5. Phép cộng các phân thức đại số có đáp ánLớp 8Toán

1 mã đề 9 câu hỏi 1 giờ

156,10312,003

Trắc nghiệm chuyên đề Toán 8 Chủ đề 4: Bất phương trình bậc nhất một ẩn (Có đáp án)Lớp 8Toán

1 mã đề 18 câu hỏi 1 giờ

147,62511,351

Trắc nghiệm chuyên đề Toán 8 Chủ đề 4: Phương trình tích có đáp ánLớp 8Toán

1 mã đề 10 câu hỏi 1 giờ

189,27014,551

Trắc nghiệm chuyên đề Toán 8 Chủ đề 10: Đường thẳng song song với một đường thẳng cho trước có đáp ánLớp 8Toán

1 mã đề 4 câu hỏi 1 giờ

162,76312,515

Trắc nghiệm chuyên đề Toán 8 Chủ đề 5: Phương trình chứa dấu giá trị tuyệt đối(Có đáp án)Lớp 8Toán

1 mã đề 21 câu hỏi 1 giờ

178,27413,702