[2021] Trường THPT Nguyễn Đăng Đạo lần 3 - Đề thi thử THPT QG năm 2021 môn Toán

Tìm tất cả các giá trị của m để hàm số $y={{x}^{3}}-3m{{x}^{2}}+mx+2$ có hai điểm cực trị.

Đường cong sau là đồ thị của hàm số nào trong các hàm số đã cho dưới đây?

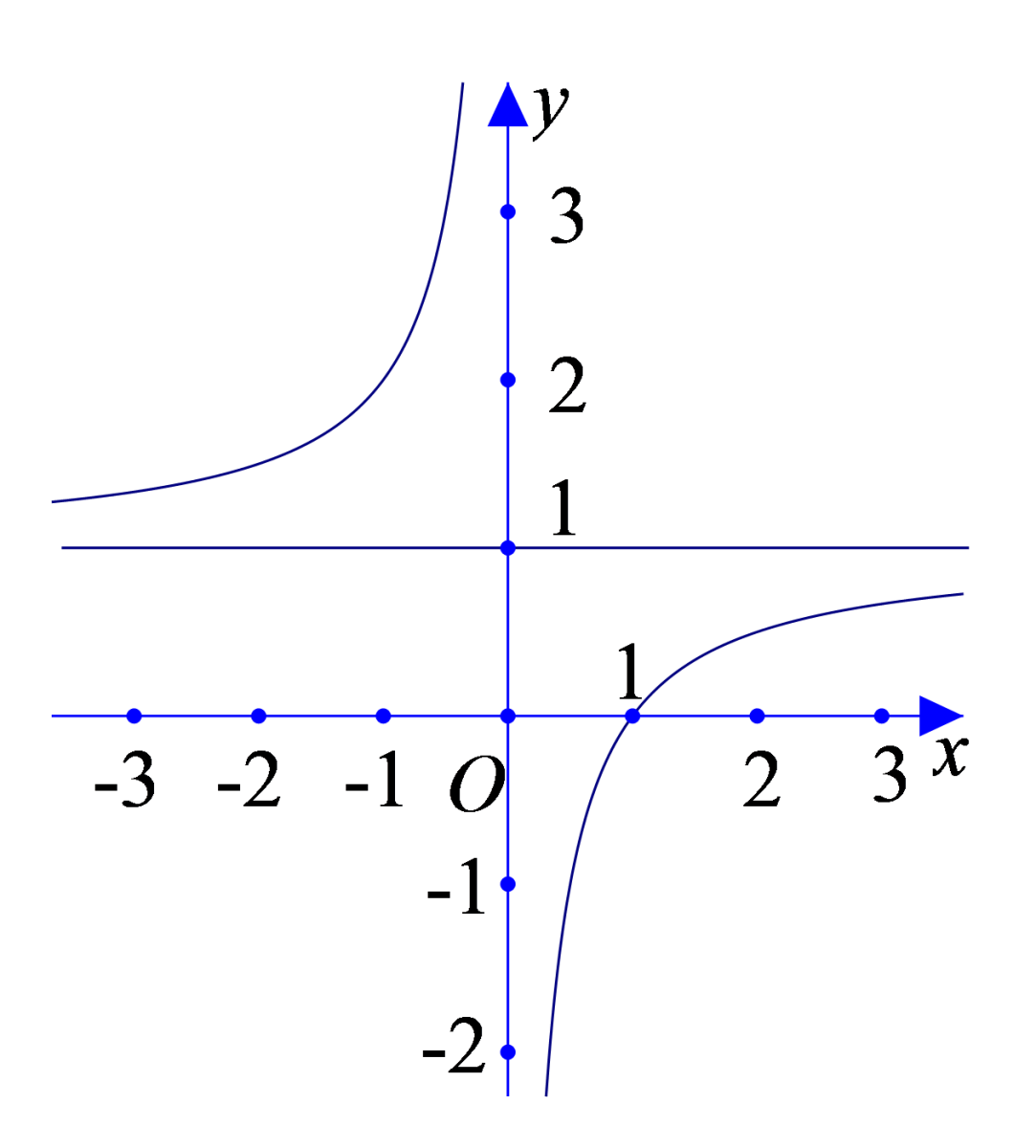
Cho hình chópS.ABCD có đáy ABCD là hình vuông cạnh 2a, SA=a,SA vuông góc với mặt đáy. Thể tích của khối chóp S.ABCD là

Cho hàm số $y={{x}^{4}}+b{{x}^{2}}+c$ có đồ thị như hình vẽ sau:

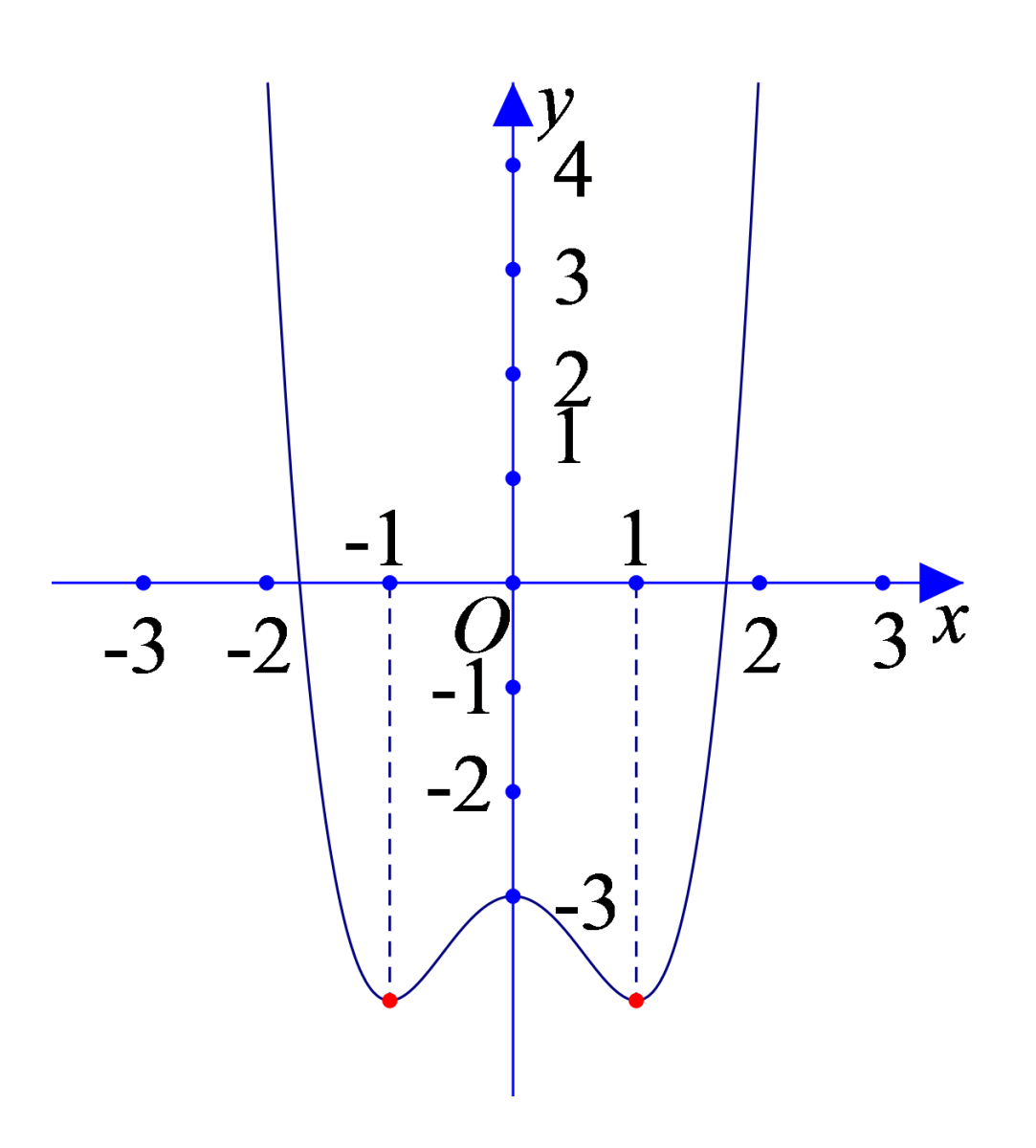
Tính tổng b+c.

Cho hàm số $y=f\left( x \right)$ có đạo hàm là ${f}'\left( x \right)={{\left( x-1 \right)}^{2}}\left( 3-x \right)\left( {{x}^{2}}-x-1 \right)$ . Hỏi hàm số $f\left( x \right)$ có bao nhiêu điểm cực tiểu?

Trong các mệnh đề sau, mệnh đề nào Sai?

Nhóm có 7 học sinh, cần chọn 3 học sinh bất kì vào đội văn nghệ số cách chọn là:

Cho hàm số $y=f\left( x \right)$ liên tục trên $\mathbb{R}$ và có bảng biến thiên như sau:

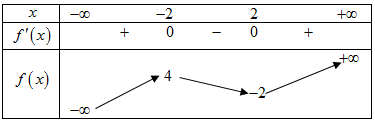
Hỏi phương trình $\frac{1}{2}f\left( x \right)-2=0$ có bao nhiêu nghiệm phân biệt?

Hàm số $y={{x}^{3}}-3{{x}^{2}}+2$ nghịch biến trên khoảng nào dưới đây?

Số tiệm cận đứng của đồ thị hàm số $y=\frac{\sqrt{x+3}-2}{{{x}^{2}}-x}$ là

Giới hạn $\underset{x\to -\infty }{\mathop{\lim }}\,\frac{\sqrt{{{x}^{2}}+x+1}}{2x+1}$ là :

Cho hàm số $y=f\left( x \right)$ có đồ thị như hình vẽ bên. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

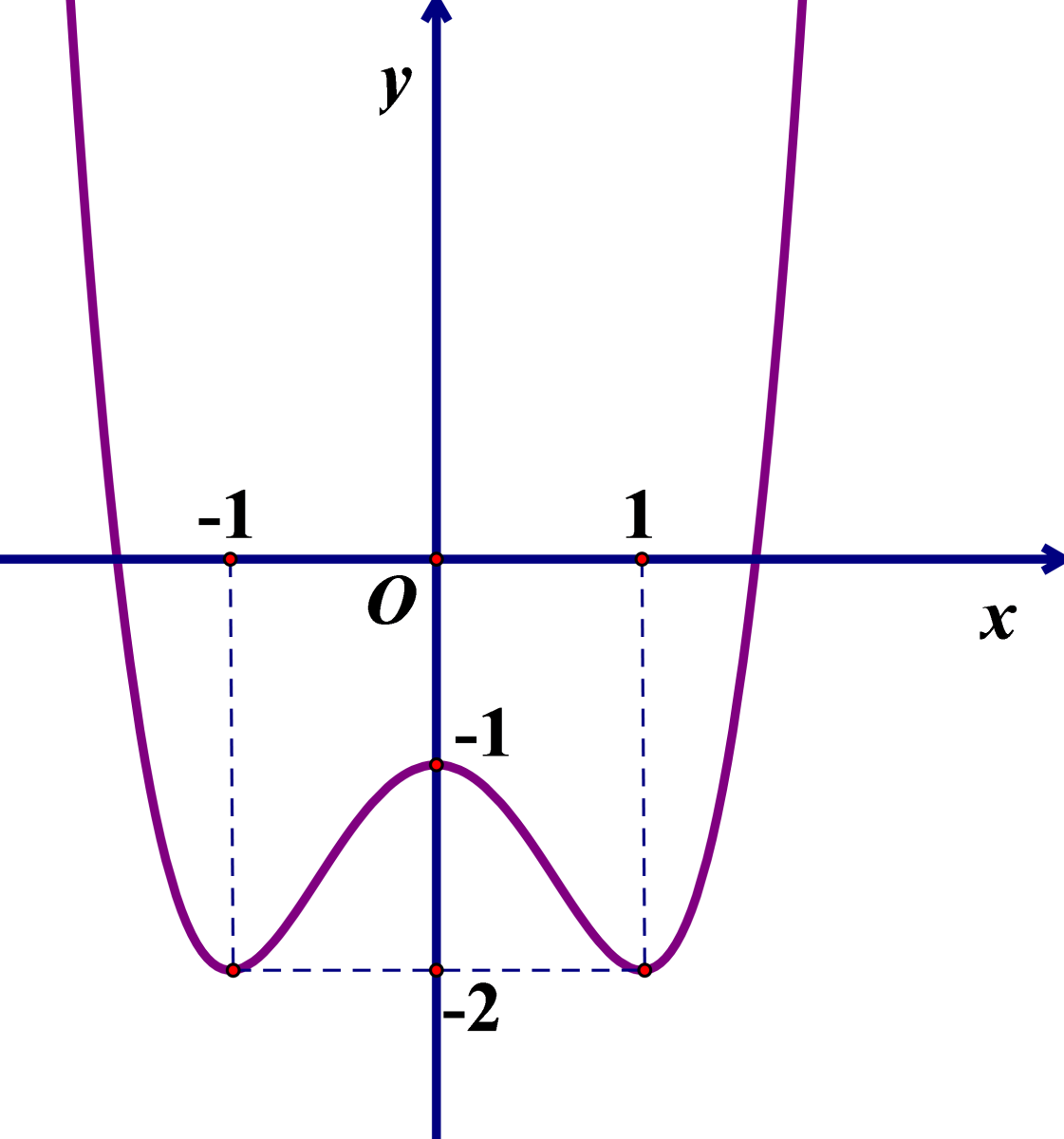
Tìm m để bất phương trình $2{{x}^{3}}-6x+2m-1\le 0$ nghiệm đúng với mọi $x\in \left[ -1;1 \right]$ .

Hộp đựng 3 bi xanh, 2 bi đỏ, 3 bi vàng. Tính xác suất để chọn được 4 bi đủ 3 màu là:

Hình bát diện đều có bao nhiêu mặt?

Cho hình chóp S.ABC có $SA\bot (ABC),\,SA=2a.$ Tam giác ABC vuông tại B $\,AB=a$ , $BC=a\sqrt{3}$ . Tính cosin của góc $\varphi$ tạo bởi hai mặt phẳng $(SBC)$ và $(ABC).$

Số nghiệm của phương trình $2\sin x=1$ trên $\left[ 0,\pi \right]$ là:

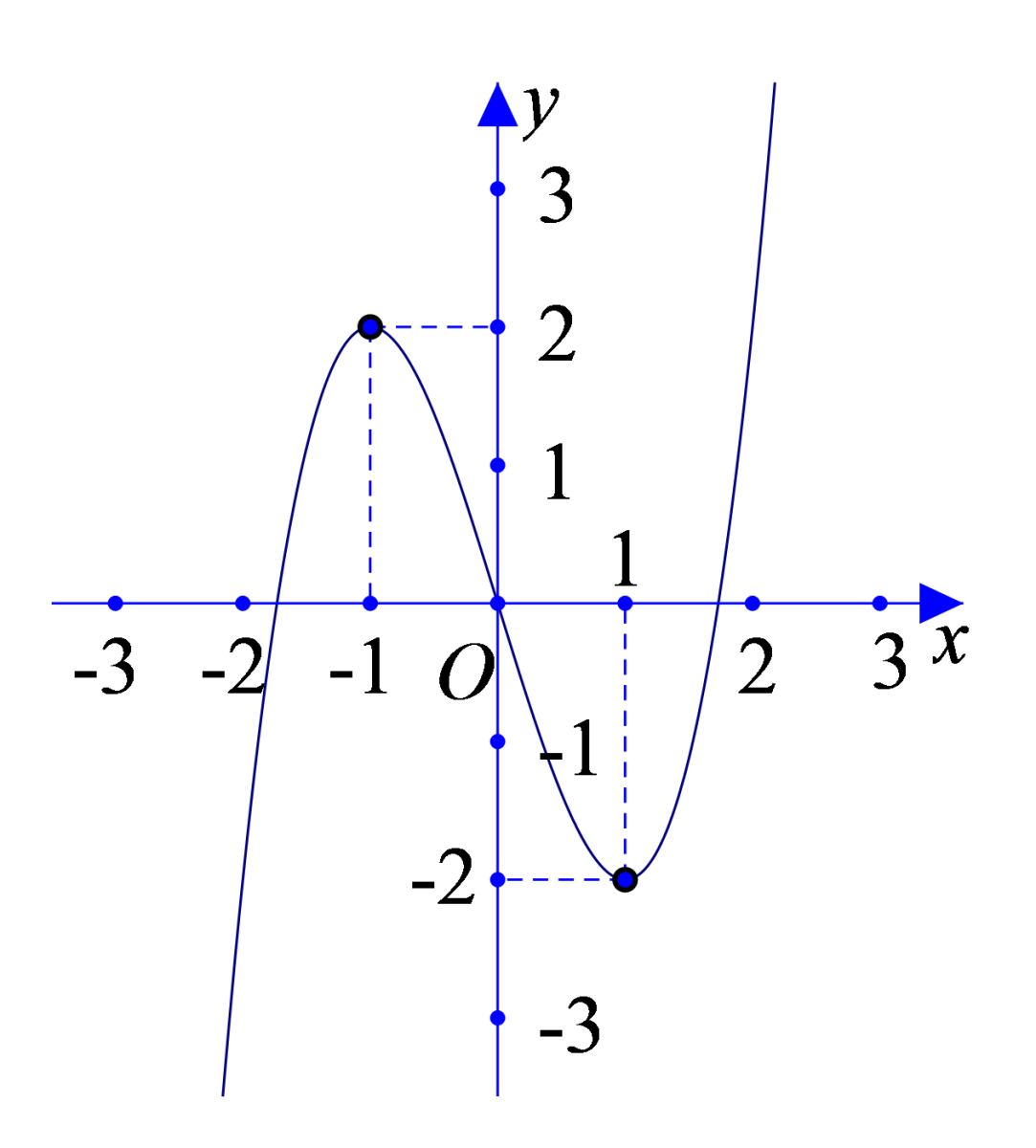
Đường cong sau là đồ thị của một trong các hàm số cho dưới đây. Đó là hàm số nào?

Tìm giá trị nhỏ nhất của hàm số $y={{x}^{3}}-6{{x}^{2}}+2$ trên đoạn $\left[ -1;2 \right]$ .

Có mấy khối đa diện trong các khối sau?

Cho hàm số $y=\frac{2x-1}{x-1}$ . Khẳng định nào sau đây đúng?

Một vật rơi tự do theo phương trình $S\left( t \right)=\frac{1}{2}g{{t}^{2}}$ trong đó $g\approx 9,8m/{{s}^{2}}$ là gia tốc trọng trường. Vận tốc tức thời tại thời điểm $t=5s$ là:

Cho khối chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$ , cạnh $SA=a\sqrt{3}$ , hai mặt bên $(SAB)$ và $(SAC)$ cùng vuông góc với mặt phẳng $(ABC)$ (tham khảo hình bên).

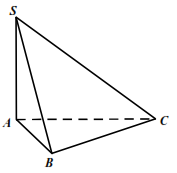
Tính thể tích V của khối hình chóp đã cho

Cho khối lăng trụ có diện tích đáy $B=8$ và chiều cao $h=6$ . Thể tích của khối lăng trụ đã cho bằng.

Cho hàm số $y=f\left( x \right)$ liên tục trên $\left[ -2;4 \right]$ và có bảng biến thiên như sau:

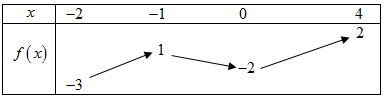
Gọi $M,\,m$ lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số $y=\left| f\left( x \right) \right|$ trên đoạn $\left[ -2;4 \right]$ . Tính ${{M}^{2}}-{{m}^{2}}$ .

Cho khai triển ${{\left( x-2 \right)}^{80}}={{a}_{0}}+{{a}_{1}}x+{{a}_{2}}{{x}^{2}}+...+{{a}_{80}}{{x}^{80}}$ . Hệ số $a_{78}$ là:

Cho hình hộp chữ nhật $ABCD.{A}'{B}'{C}'{D}'$ có $AB=2a, AD=3a, A{A}'=3a$ . $E$ thuộc cạnh ${B}'{C}'$ sao cho ${B}'E=3{C}'E$ . Thể tích khối chóp E.BCD bằng:

Cho hàm số $y=f\left( x \right)$ liên tục trên $\mathbb{R}$ và có bảng xét dấu đạo hàm như sau:

Giá trị nhỏ nhất của hàm số đã cho trên đoạn $\left[ -1;1 \right]$ là:

Đường thẳng nào dưới đây là tiệm cận đứng của đồ thị hàm số $y=\frac{2x-1}{x-1}\text{ }?$

Hàm số $y=\frac{3\sin x+5}{1-c\text{os}x}$ xác định khi :

Trong các dãy số sau dãy nào là cấp số cộng $\left( n\ge 1,n\in \mathbb{N} \right)$ ?

Công thức tính thể tích V của khổi chóp có diện tích đáy B và chiều cao h là

Cho hàm số $y=f\left( x \right)$ liên tục trên $\mathbb{R}$ và có bảng biến thiên như sau:

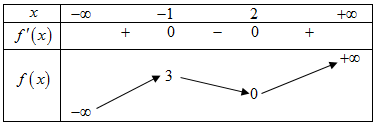
Điểm cực tiểu của hàm số đã cho là:

Cho khối hộp chữ nhật có độ dài chiều rộng, chiều dài, chiều cao lần lượt là $3a;\,4a;\,5a$ . Thể tích của khối hộp chữ nhật đã cho bằng

Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB>AD. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi $M,\,N$ lần lượt là trung điểm của AB và BC. Xét các mệnh đề sau:

(i). $SM\bot \left( ABCD \right)$ .

(ii). $BC\bot \left( SAB \right)$ .

(iii). $AN\bot \left( SDM \right)$ .

Trong các mệnh đề trên, có bao nhiêu mệnh đề đúng?

Cho hàm số bậc ba $y=f\left( x \right)$ có đồ thị như sau:

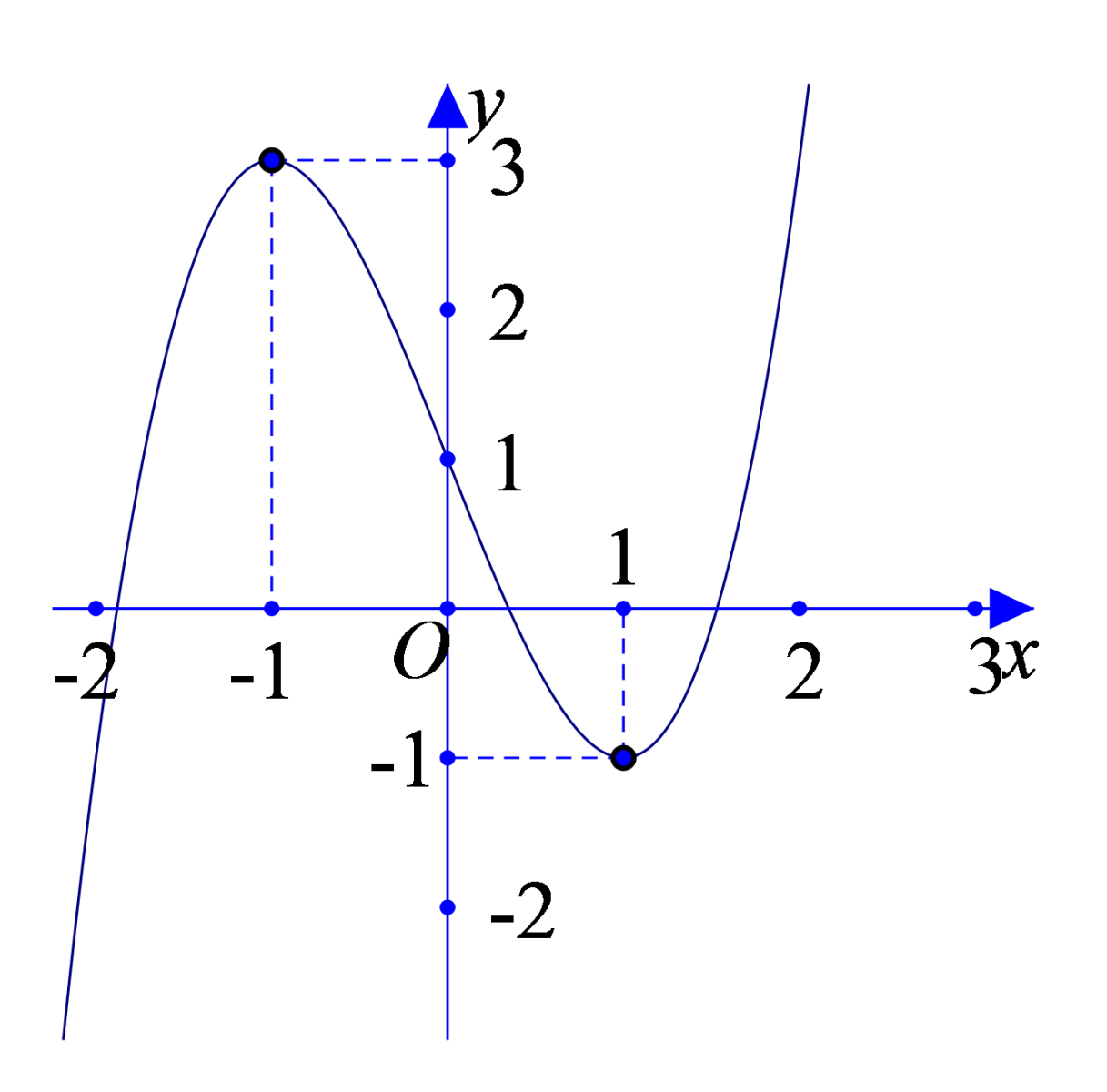
Hỏi hàm số $g\left( x \right)=2{{\left[ f\left( x \right) \right]}^{3}}-\frac{1}{2}{{\left[ f\left( x \right) \right]}^{2}}-12f\left( x \right)+3$ có bao nhiêu điểm cực trị?

Cho hình lăng trụ đứng $ABC.{A}'{B}'{C}'$ có $\widehat{BAC}={{120}^{0}}$ , $BC=A{A}'=a$ . Gọi M là trung điểm của $C{C}'$ . Tính khoảng cách giứa hai đường thẳng BM và $A{B}'$ , biết rằng chúng vuông góc với nhau.

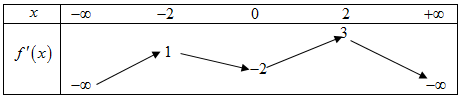
Cho hàm số $y=f\left( x \right)=a{{x}^{3}}+b{{x}^{2}}+cx+d$ . Biết rằng đồ thị hàm số cắt trục Ox tại ba điểm phân biệt có hoành độ là $-1,\,\frac{1}{3},\,\frac{1}{2}$ . Hỏi phương trình $f\left[ \sin \left( {{x}^{2}} \right) \right]=f\left( 0 \right)$ có bao nhiêu nghiệm phân biệt thuộc đoạn $\left[ -\sqrt{\pi };\sqrt{\pi } \right]$ .

Cho hàm số $y=f\left( x \right)$ có đạo hàm liên tục trên $\mathbb{R}$ và có bảng biến thiên của hàm số $y={f}'\left( x \right)$ như sau:

Tìm tất cả các giá trị của tham số m để bất phương trình $f\left( x \right)+\frac{1}{4}{{x}^{4}}-{{x}^{3}}-3x-m\ge 0$ nghiệm đúng với mọi $x\in \left( -2;2 \right)$ .

Có bao nhiêu giá trị nguyên thuộc đoạn $\left[ -10;10 \right]$ của $m$ để giá trị lớn nhất của hàm số $y=\frac{2x+m}{x+1}$ trên đoạn $\left[ -4;-2 \right]$ không lớn hơn 1?

Cho khối chóp $S.ABCD$ , đáy $ABCD$ là hình chữ nhật có diện tích bằng $3\sqrt{2}{{a}^{2}}$ , $M$ là trung điểm của $BC$ , $AM$ vuông góc với $BD$ tại $H$ , $SH$ vuông góc với mặt phẳng $\left( ABCD \right)$ , khoảng cách từ điểm D đến mặt phẳng $\left( SAC \right)$ bằng $a$ . Thể tích V của khối chóp đã cho là

Cho hình hộp chữ nhật $ABCD.{A}'{B}'{C}'{D}'$ có $AB=4a;\,\,BC=2a;\,\,A{A}'=2a$ . Tính sin của góc giữa đường thẳng $B{D}'$ và mặt phẳng $\left( {A}'{C}'D \right)$ .

Có bao nhiêu tiếp tuyến của đồ thị hàm số $y=\frac{x}{x+1}$ mà tiếp tuyến đó tạo với hai trục tọa độ một tam giác vuông cân?

Cho hàm số $y=a{{x}^{3}}+b{{x}^{2}}+cx+d$ có đồ thị như hình vẽ sau:

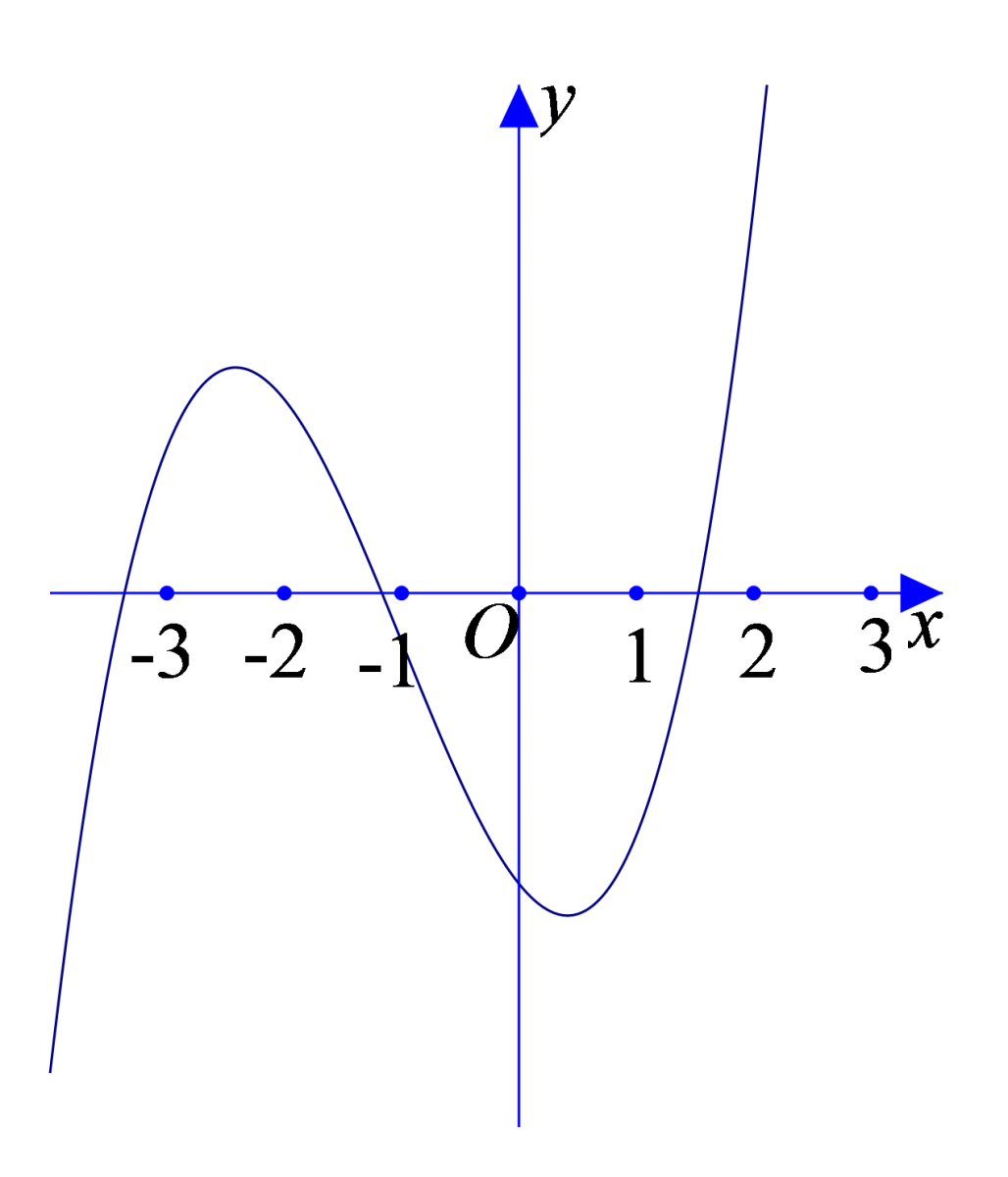
Hỏi trong các số $a,\,b,\,c,\,d$ có bao nhiêu số dương?

Tập hợp tất cả các giá trị của tham số thực m để hàm số $y=-{{x}^{3}}+3{{x}^{2}}+\left( m-2 \right)x+2$ nghịch biến trên khoảng $\left( -\infty ;2 \right)$ là

Cho hàm số $y=f\left( x \right)$ có đạo hàm liên tục trên $\mathbb{R}$ . Đồ thị hàm số $y={f}'\left( {{x}^{3}}+x+2 \right)$ như hình vẽ sau:

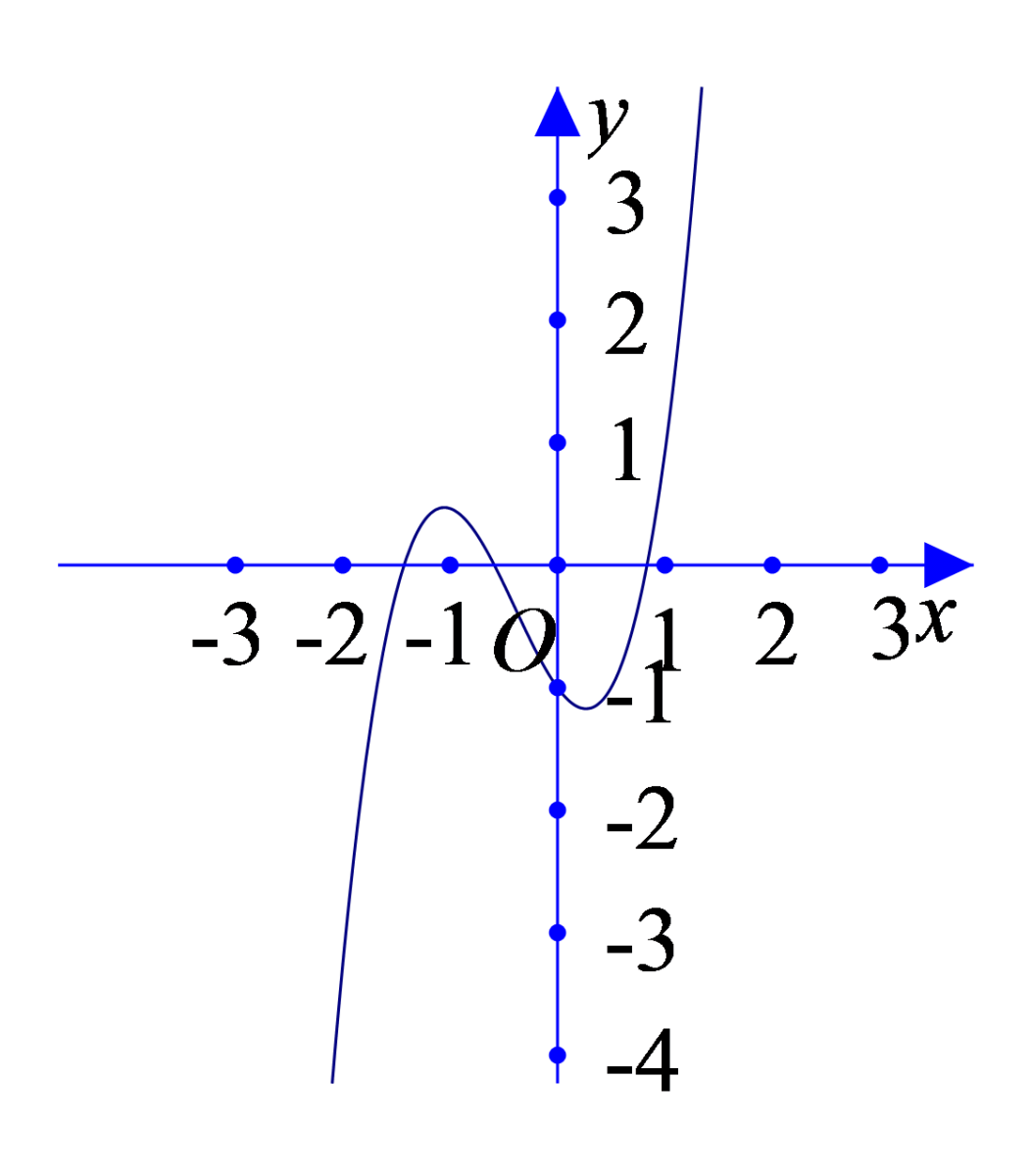
Hỏi hàm số $y=f\left( \left| x \right| \right)$ có bao nhiêu điểm cực trị?

Cho dãy số $\left( {{u}_{n}} \right)$ thỏa mãn: $u_{1}^{2}-4\left( {{u}_{1}}+{{u}_{n-1}}{{u}_{n}}-1 \right)+4u_{n-1}^{2}+u_{n}^{2}=0,\,\forall n\ge 2,\,n\in \mathbb{N}$ . Tính ${{u}_{5}}$ .

Đồ thị hàm số $y=\frac{x+1}{2x+4}$ có tiệm cận ngang là đường thẳng nào trong các đường thẳng sau ?

Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như sau

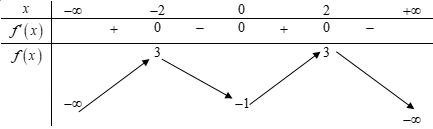
Hàm số $y=f\left( {{x}^{2}}-2 \right)$ đồng biến trên khoảng nào dưới đây?

Cho hình lăng trụ $ABC.{A}'{B}'{C}'$ có thể tích là V. Gọi $M,\,N,\,P$ là trung điểm các cạnh $A{A}',\,AB,\,{B}'{C}'$ . Mặt phẳng $\left( MNP \right)$ chia khối lăng trụ thành hai phần. Tính thể tích phần chứa đỉnh B theo V.