Trang chủ Đề thi [2021] Trường THPT Nguyễn Văn Linh - Đề thi thử THPT QG năm 2021 môn Toán
thumbnail

[2021] Trường THPT Nguyễn Văn Linh - Đề thi thử THPT QG năm 2021 môn Toán

Đề thi thử THPT Quốc gia môn Toán năm 2021 từ Trường THPT Nguyễn Văn Linh, miễn phí với đáp án chi tiết. Đề thi bao gồm các dạng bài tập trọng tâm như logarit, tích phân, số phức và hình học không gian, giúp học sinh rèn luyện toàn diện kỹ năng giải toán.

Từ khoá: Toán học đề thi thử 2021 Trường THPT Nguyễn Văn Linh logarit tích phân số phức hình học không gian đề thi có đáp án luyện thi THPT Quốc gia

Thời gian làm bài: 1 giờ

Đề thi nằm trong bộ sưu tập: 📘 Tuyển Tập Bộ 500 Đề Thi Ôn Luyện Môn Toán THPT Quốc Gia Các Tỉnh Từ Năm 2018-2025 - Có Đáp Án Chi Tiết


Bạn chưa làm đề thi này!!!

Hãy bắt đầu chinh phục nào!



 

Xem trước nội dung:

Câu 1: 1 điểm

Có bao nhiêu cách chọn ba học sinh từ một nhóm gồm 15 học sinh?

A.  
153
B.  
315
C.  
A153.A_{15}^3.
D.  
C153.C_{15}^3.
Câu 2: 1 điểm

Cho cấp số cộng (un) biết u1=3,u2=−1.{u_1} = 3,{u_2} = - 1. Tìm u3.

A.  
4
B.  
2
C.  
-5
D.  
7
Câu 3: 1 điểm

Cho hàm số y = f(x) có bảng biến thiên như hình bên. Mệnh đề nào sau đây là đúng?

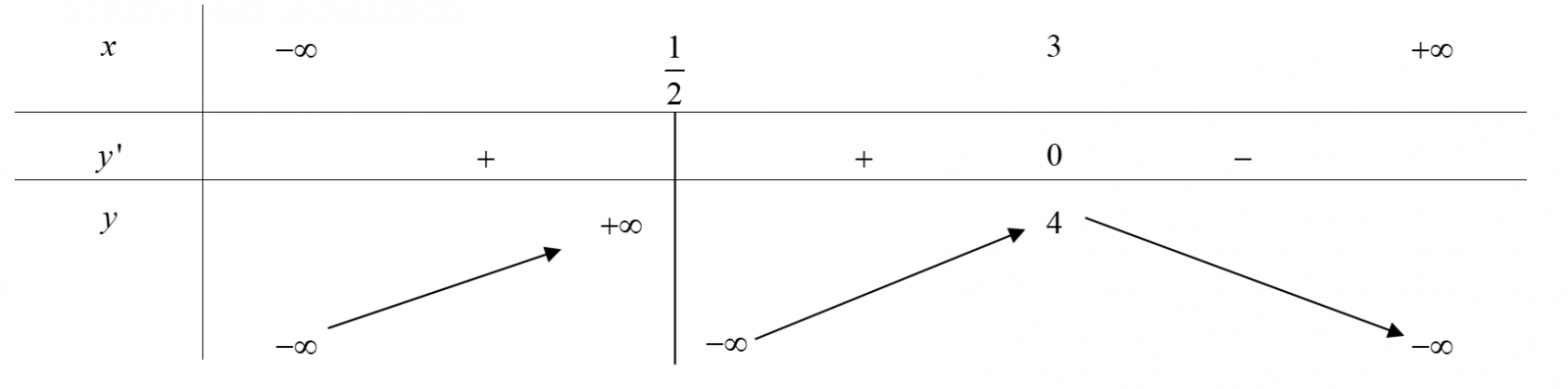
Hình ảnh

A.  
Hàm số đã cho đồng biến trên các khoảng (−∞;−12)\left( -\infty ;-\frac{1}{2} \right) và (3;+∞).\left( 3;+\infty \right).
B.  
Hàm số đã cho đồng biến trên khoảng (−12;+∞).\left( -\frac{1}{2};+\infty \right).
C.  
Hàm số đã cho nghịch biến trên khoảng (3;+∞).\left( 3;+\infty \right).
D.  
Hàm số đã cho đồng biến trên khoảng (−∞;3).\left( -\infty ;3 \right).
Câu 4: 1 điểm

Cho hàm số y = f(x) có bảng biến thiên như hình vẽ dưới đây. Hàm số đạt cực đại tại điểm

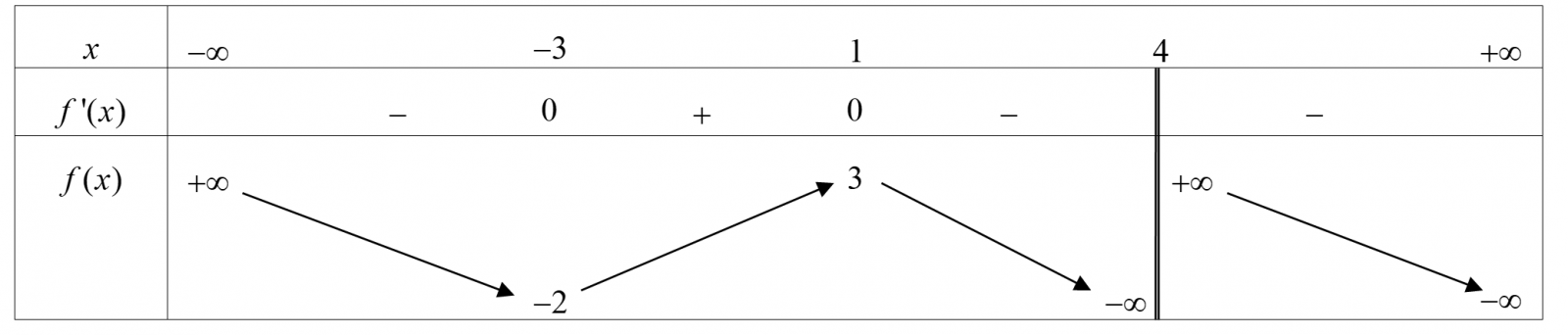
Hình ảnh

A.  
x = 3
B.  
x = -3
C.  
x = 1
D.  
x = 4
Câu 5: 1 điểm

Cho hàm số y = f(x). Hàm số y = f'(x) có đồ thị như hình bên. Tìm số điểm cực trị của hàm số y = f(x)

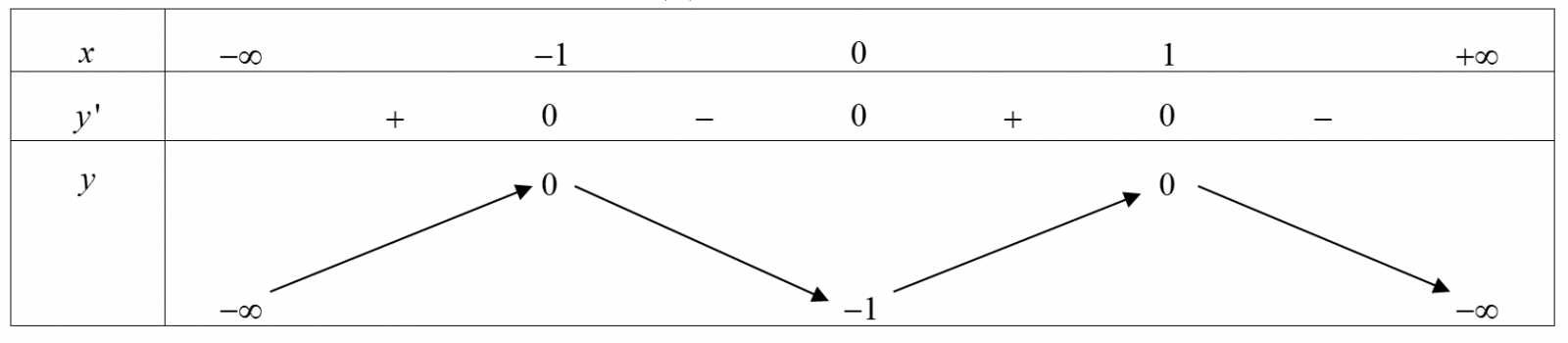
Hình ảnh

A.  
3
B.  
1
C.  
0
D.  
2
Câu 6: 1 điểm

Cho bảng biến thiên của hàm số y = f(x). Mệnh đề nào sau đây sai?

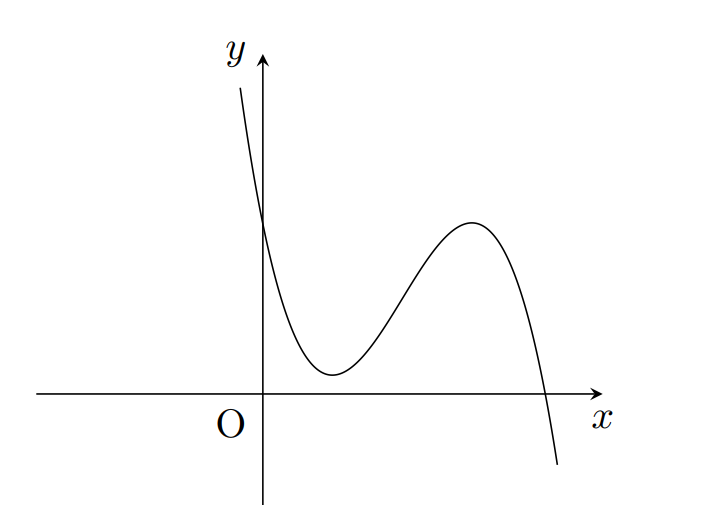
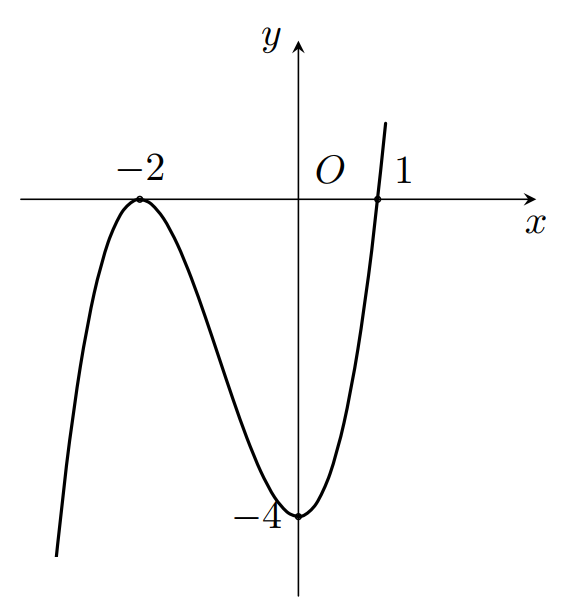
Hình ảnh

A.  
Hàm số y=f(x)y=f\left( x \right) nghịch biến trên (−1;0)\left( -1;0 \right) và (1;+∞).\left( 1;+\infty \right).
B.  
Giá trị nhỏ nhất của hàm số y=f(x)y=f\left( x \right) trên tập R bằng -1.
C.  
Giá trị lớn nhất của hàm số y=f(x)y=f\left( x \right) trên tập R bằng 0.
D.  
Đồ thị hàm số y=f(x)y=f\left( x \right) không có đường tiệm cận.
Câu 7: 1 điểm

Đường cong trong hình vẽ là đồ thị của hàm số nào dưới đây?

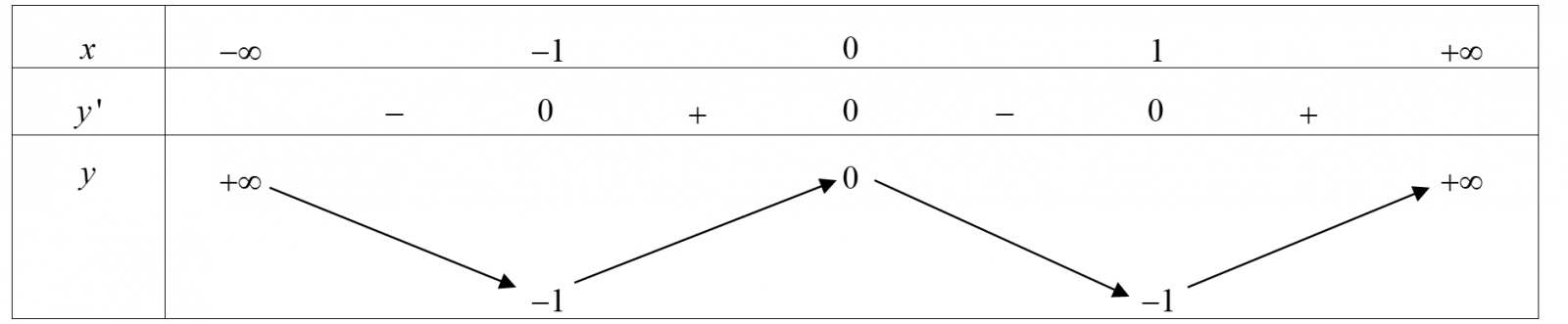
Hình ảnh

A.  
y=x−4x+1.y = \frac{{x - 4}}{{x + 1}}.
B.  
y=x3+3x2−4y = {x^3} + 3{x^2} - 4
C.  
y=x4+3x2−4.y = {x^4} + 3{x^2} - 4.
D.  
y=x3+6x2−4.y = {x^3} + 6{x^2} - 4.
Câu 8: 1 điểm

Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên sau

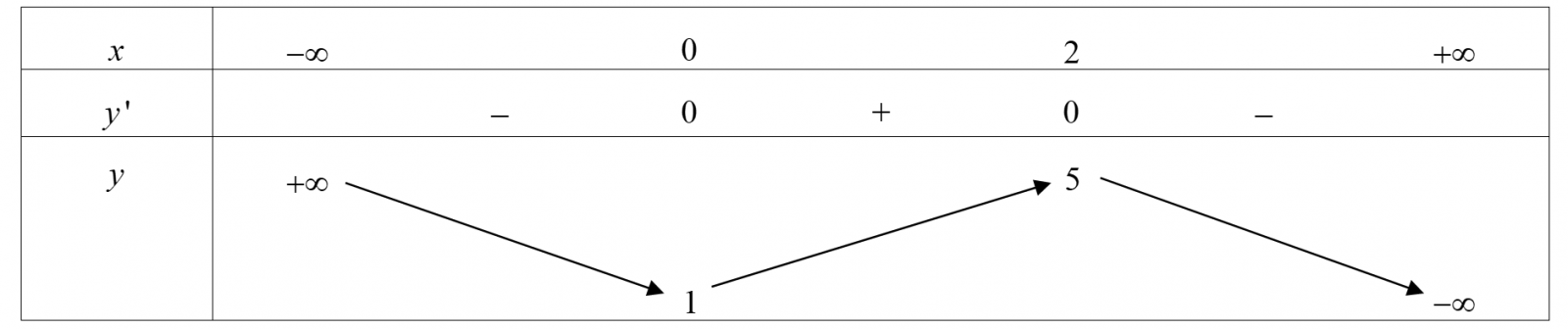
Hình ảnh

Tìm tất cả các giá trị thực của tham số m để phương trình f(x)−1=mf\left( x \right) - 1 = m có đúng hai nghiệm.

A.  
-2 < m < -1
B.  
m=−2,m≥−1.m = - 2,m \ge - 1.
C.  
m > 0,m = - 1.
D.  
m = - 2,m > - 1.
Câu 9: 1 điểm

Cho a, b, c > 0 và ae1.a e 1. Khẳng định nào sau đây là khẳng định sai?

A.  
log⁡ab=c⇔b=ac.{\log _a}b = c \Leftrightarrow b = {a^c}.
B.  
log⁡a(bc)=log⁡ab−log⁡ac.{\log _a}\left( {\frac{b}{c}} \right) = {\log _a}b - {\log _a}c.
C.  
log⁡a(bc)=log⁡ab+log⁡ac.{\log _a}\left( {bc} \right) = {\log _a}b + {\log _a}c.
D.  
log⁡a(b+c)=log⁡ab+log⁡ac.{\log _a}\left( {b + c} \right) = {\log _a}b + {\log _a}c.
Câu 10: 1 điểm

Hệ số góc tiếp tuyến của đồ thị hàm số y=log⁡3xy = {\log _3}x tại điểm có hoành độ x = 2 bằng

A.  
1ln⁡3.\frac{1}{{\ln 3}}.
B.  
ln3
C.  
12ln⁡3.\frac{1}{{2\ln 3}}.
D.  
2ln3
Câu 11: 1 điểm

Rút gọn biểu thức P=x13x6P = {x^{\frac{1}{3}}}\sqrt[6]{x} với x > 0

A.  
P=x.P = \sqrt x .
B.  
P=x18.P = {x^{\frac{1}{8}}}.
C.  
P=x29.P = {x^{\frac{2}{9}}}.
D.  
P=x2P = {x^2}
Câu 12: 1 điểm

Tìm nghiệm x0 của phương trình 32x+1=21.{3^{2x + 1}} = 21.

A.  
x0=log⁡921.{x_0} = {\log _9}21.
B.  
x0=log⁡218.{x_0} = {\log _{21}}8.
C.  
x0=log⁡213.{x_0} = {\log _{21}}3.
D.  
x0=log⁡97.{x_0} = {\log _9}7.
Câu 13: 1 điểm

Phương trình log⁡2(x−1)=1{\log _2}\left( {x - 1} \right) = 1 có nghiệm là

A.  
x = 4
B.  
x = 3
C.  
x = 2
D.  
x = 1
Câu 14: 1 điểm

Cho hàm số f(x) = x3 có một nguyên hàm là F(x). Khẳng định nào sau đây là đúng?

A.  
F(2)−F(0)=16.F\left( 2 \right) - F\left( 0 \right) = 16.
B.  
F(2)−F(0)=1.F\left( 2 \right) - F\left( 0 \right) = 1.
C.  
F(2)−F(0)=8.F\left( 2 \right) - F\left( 0 \right) = 8.
D.  
F(2)−F(0)=4.F\left( 2 \right) - F\left( 0 \right) = 4.
Câu 15: 1 điểm

Nguyên hàm của hàm số f(x)=cos⁡3xf\left( x \right) = \cos 3x là

A.  
- sin 3x + C.
B.  
13sin⁡3x+C\frac{1}{3}\sin 3x + C
C.  
−13sin⁡3x+C-\frac{1}{3}\sin 3x + C
D.  
−3sin⁡3x+C - 3\sin 3x + C
Câu 16: 1 điểm

Trong không gian Oxyz cho hình bình hành ABCD có A(1;0;1),B(0;2;3),D(2;1;0).A\left( {1;0;1} \right),B\left( {0;2;3} \right),D\left( {2;1;0} \right). Khi đó diện tích của hình bình hành ABCD bằng

A.  
26\sqrt {26}
B.  
262\frac{{\sqrt {26} }}{2}
C.  
52\frac{5}{2}
D.  
5
Câu 17: 1 điểm

Cho các hàm số f(x) và F(x) liên tục trên R thỏa F′(x)=f(x),∀x∈R.F'\left( x \right) = f\left( x \right),\forall x \in R. Tính ∫01f(x)dx\int\limits_0^1 {f\left( x \right)dx} biết F(0)=2,F(1)=5.F\left( 0 \right) = 2,F\left( 1 \right) = 5.

A.  
∫01f(x)dx=−3.\int\limits_0^1 {f\left( x \right)dx} = - 3.
B.  
∫01f(x)dx=7.\int\limits_0^1 {f\left( x \right)dx} = 7.
C.  
∫01f(x)dx=1.\int\limits_0^1 {f\left( x \right)dx} = 1.
D.  
∫01f(x)dx=3.\int\limits_0^1 {f\left( x \right)dx} = 3.
Câu 18: 1 điểm

Cho số phức z = 7 - 5i. Tìm phần thực a của z

A.  
a = -7
B.  
a = 5
C.  
a = -5
D.  
a = 7
Câu 19: 1 điểm

Cho i là đơn vị ảo. Giá trị của biểu thức z=(1+i)2z = {\left( {1 + i} \right)^2} là

A.  
2i
B.  
-i
C.  
-2i
D.  
i
Câu 20: 1 điểm

Trong mặt phẳng Oxy số phức z = 2i -1 được biểu diễn bởi điểm M có tọa độ là

A.  
(1;-2)
B.  
(2;1)
C.  
(2;-1)
D.  
(-1;2)
Câu 21: 1 điểm

Tính thể tích khối chóp tứ giác đều cạnh đáy bằng a chiều cao bằng 3a.

A.  
V = a3
B.  
V=a33.V = \frac{{{a^3}}}{3}.
C.  
V=a334.V = \frac{{{a^3}\sqrt 3 }}{4}.
D.  
V=a3312.V = \frac{{{a^3}\sqrt 3 }}{{12}}.
Câu 22: 1 điểm

Khối lăng trụ có diện tích đáy bằng 24(cm2),24\left( {c{m^2}} \right), chiều cao bằng 3(cm) thì có thể tích bằng

A.  
72(cm3).72\left( {c{m^3}} \right).
B.  
126(cm3).126\left( {c{m^3}} \right).
C.  
24(cm3).24\left( {c{m^3}} \right).
D.  
8(cm3).8\left( {c{m^3}} \right).
Câu 23: 1 điểm

Tính thể tích của khối trụ có bán kính đáy bằng a và độ dài đường sinh bằng a3.a\sqrt 3 .

A.  
πa33.\pi {a^3}\sqrt 3 .
B.  
πa333.\frac{{\pi {a^3}\sqrt 3 }}{3}.
C.  
3πa33\pi {a^3}
D.  
πa23.\pi {a^2}\sqrt 3 .
Câu 24: 1 điểm

Cho một hình trụ có chiều cao bằng 2 và bán kính đáy bằng 3. Thể tich của khối trụ đã cho bằng

A.  
6π6\pi
B.  
18π18\pi
C.  
15π15\pi
D.  
9π9\pi
Câu 25: 1 điểm

Trong không gian với hệ tọa độ Oxyz tìm tọa độ u→\overrightarrow u biết u→=2i→−3j→+5k→.\overrightarrow u = 2\overrightarrow i - 3\overrightarrow j + 5\overrightarrow k .

A.  
u→=(5;−3;2).\overrightarrow u = \left( {5; - 3;2} \right).
B.  
u→=(2;−3;5).\overrightarrow u = \left( {2; - 3;5} \right).
C.  
u→=(2;5;−3).\overrightarrow u = \left( {2;5; - 3} \right).
D.  
u→=(−3;5;2).\overrightarrow u = \left( { - 3;5;2} \right).
Câu 26: 1 điểm

Trong không gian với hệ tọa độ Oxyz tâm I của mặt cầu (S):x2+y2+z2−8x−2y+1=0\left( S \right):{x^2} + {y^2} + {z^2} - 8x - 2y + 1 = 0 có tọa độ là

A.  
I(4;1;0)
B.  
I(4;-1;0)
C.  
I(-4;1;0)
D.  
I(-4;-1;0)
Câu 27: 1 điểm

Trong không gian Oxyz phương trình nào dưới đây là phương trình mặt phẳng đi qua điểm M(3;-1;1) và có véc-tơ pháp tuyến n→=(3;−2;1)?\overrightarrow n = \left( {3; - 2;1} \right)?

A.  
x - 2y + 3z + 13 = 0.
B.  
3x + 2y + z - 8 = 0
C.  
3x - 2y + z + 12 = 0
D.  
3x - 2y + z - 12 = 0
Câu 28: 1 điểm

Trong không gian Oxyz phương trình nào dưới đây là phương trình chính tắc của đường thẳng {x=1−2ty=3tz=2+t?\left\{ \begin{array}{l}x = 1 - 2t\\y = 3t\\z = 2 + t\end{array} \right.?

A.  
x−11=y3=z+22.\frac{{x - 1}}{1} = \frac{y}{3} = \frac{{z + 2}}{2}.
B.  
x+11=y3=z−22.\frac{{x + 1}}{1} = \frac{y}{3} = \frac{{z - 2}}{2}.
C.  
x+1−2=y3=z−21.\frac{{x + 1}}{{ - 2}} = \frac{y}{3} = \frac{{z - 2}}{1}.
D.  
x−1−2=y3=z−21.\frac{{x - 1}}{{ - 2}} = \frac{y}{3} = \frac{{z - 2}}{1}.
Câu 29: 1 điểm

Trên mặt phẳng, cho hình vuông có cạnh bằng 2. Chọn ngẫu nhiên một điểm thuộc hình vuông đã cho (kể cả các điểm nằm trên cạnh của hình vuông). Gọi P là xác suất để điểm được chọn thuộc vào hình tròn nội tiếp hình vuông đã cho (kể cả các điểm nằm trên đường tròn nội tiếp hình vuông), giá trị gần nhất của P là

A.  
0,242
B.  
0,215
C.  
0,785
D.  
0,758
Câu 30: 1 điểm

Hàm số y=x4−2x2y = {x^4} - 2{x^2} có đồ thị nào dưới đây?

A.  
A.
B.  
B.
C.  
C.
D.  
D.
Câu 31: 1 điểm

Giá trị lớn nhất của hàm số y=x4−3x2+2y = {x^4} - 3{x^2} + 2 trên đoạn [0;3] bằng:

A.  
57
B.  
55
C.  
56
D.  
54
Câu 32: 1 điểm

Cho hàm số y = f(x) có bảng biến thiên như hình bên. Có bao nhiêu giá trị nguyên dương của m để phương trình f(x)=log⁡2mf\left( x \right) = {\log _2}m có ba nghiệm phân biệt.

Hình ảnh

A.  
28
B.  
29
C.  
31
D.  
30
Câu 33: 1 điểm

Biết F(x) là một nguyên hàm của hàm số f(x)=sin⁡2xf\left( x \right) = \sin 2x và F(π4)=1.F\left( {\frac{\pi }{4}} \right) = 1. Tính F(π6).F\left( {\frac{\pi }{6}} \right).

A.  
F(π6)=54.F\left( {\frac{\pi }{6}} \right) = \frac{5}{4}.
B.  
F(π6)=0.F\left( {\frac{\pi }{6}} \right) = 0.
C.  
F(π6)=34.F\left( {\frac{\pi }{6}} \right) = \frac{3}{4}.
D.  
F(π6)=12.F\left( {\frac{\pi }{6}} \right) = \frac{1}{2}.
Câu 34: 1 điểm

Tìm số phức thỏa mãn i(z‾−2+3i)=1+2i.i\left( {\overline z - 2 + 3i} \right) = 1 + 2i.

A.  
z = - 4 + 4i.
B.  
z = - 4 - 4i.
C.  
z = 4 - 4i.
D.  
z = 4 + 4i.
Câu 35: 1 điểm

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B,BC=a3,AC=2a.B,BC = a\sqrt 3 ,AC = 2a. Cạnh bên SA vuông góc với mặt phẳng đáy và SA=a3.SA = a\sqrt 3 . Góc giữa đường thẳng AB và mặt phẳng đáy bằng

A.  
45o
B.  
30o
C.  
60o
D.  
90o
Câu 36: 1 điểm

Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a cạnh bên bằng SA vuông góc với đáy, SA = a. Tính khoảng cách từ A đến mặt phẳng (SBC).

A.  
d=a32.d = \frac{{a\sqrt 3 }}{2}.
B.  
d=a22.d = \frac{{a\sqrt 2 }}{2}.
C.  
d=a62.d = \frac{{a\sqrt 6 }}{2}.
D.  
d=a63.d = \frac{{a\sqrt 6 }}{3}.
Câu 37: 1 điểm

Trong không gian với hệ tọa độ Oxyz. Viết phương trình mặt cầu đi qua A(2;3;−3),B(2;−2;2),C(3;3;4)A\left( {2;3; - 3} \right),B\left( {2; - 2;2} \right),C\left( {3;3;4} \right) và có tâm nằm trên mặt phẳng (Oxy)

A.  
(x−6)2+(y−1)2+z2=29.{\left( {x - 6} \right)^2} + {\left( {y - 1} \right)^2} + {z^2} = 29.
B.  
(x+6)2+(y+1)2+z2=29{\left( {x + 6} \right)^2} + {\left( {y + 1} \right)^2} + {z^2} = 29
C.  
(x−6)2+(y−1)2+z2=29{\left( {x - 6} \right)^2} + {\left( {y - 1} \right)^2} + {z^2} = \sqrt {29}
D.  
(x+6)2+(y+1)2+z2=29{\left( {x + 6} \right)^2} + {\left( {y + 1} \right)^2} + {z^2} = \sqrt {29}
Câu 38: 1 điểm

Trong không gian với hệ tọa độ Oxyz cho đường thẳng (d):{x=3−ty=−1+2tz=−3t(t∈R).\left( d \right):\left\{ \begin{array}{l}x = 3 - t\\y = - 1 + 2t\\z = - 3t\end{array} \right.\left( {t \in R} \right). Phương trình nào dưới đây là phương trình chính tắc của đường thẳng (d)?

A.  
x−3−1=y+12=z−3.\frac{{x - 3}}{{ - 1}} = \frac{{y + 1}}{2} = \frac{z}{{ - 3}}.
B.  
x+3−1=y−12=z−3.\frac{{x + 3}}{{ - 1}} = \frac{{y - 1}}{2} = \frac{z}{{ - 3}}.
C.  
x+13=y−2−1=z−3−3.\frac{{x + 1}}{3} = \frac{{y - 2}}{{ - 1}} = \frac{{z - 3}}{{ - 3}}.
D.  
x−3−1=y+12=z−3−3.\frac{{x - 3}}{{ - 1}} = \frac{{y + 1}}{2} = \frac{{z - 3}}{{ - 3}}.
Câu 39: 1 điểm

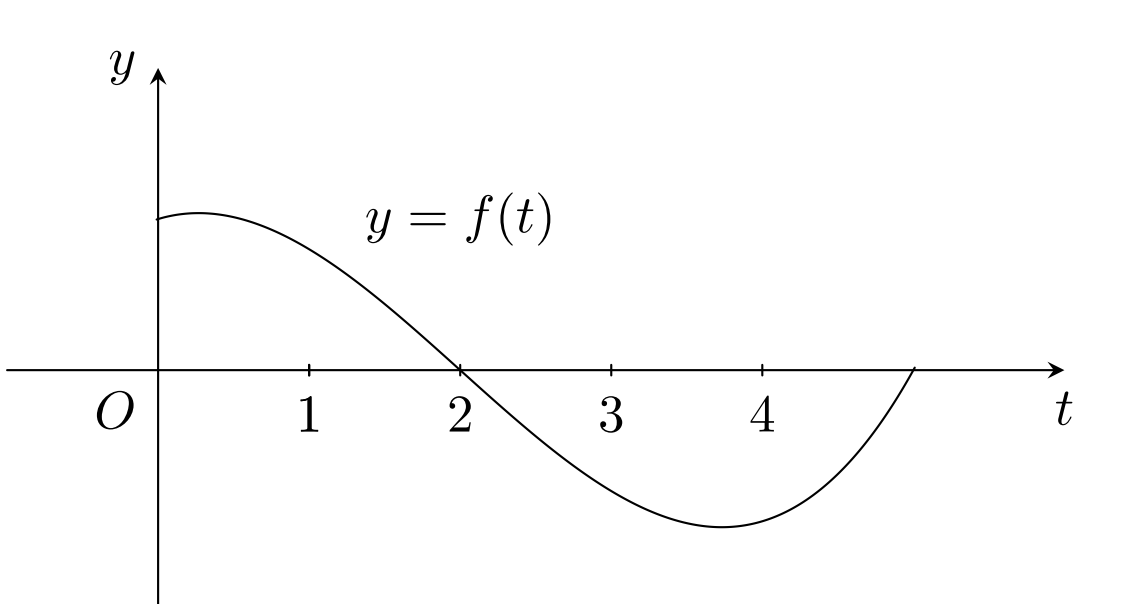
Xét hàm số F(x)=∫2xf(t)dtF\left( x \right) = \int\limits_2^x {f\left( t \right)dt} trong đó hàm số y=f(t)y = f\left( t \right) có đồ thị như hình vẽ bên. Trong các giá trị dưới đây, giá trị nào là lớn nhất?

Hình ảnh

A.  
F(1)
B.  
F(2)
C.  
F(3)
D.  
F(0)
Câu 40: 1 điểm

Tập hợp tất cả các số thực x không thỏa mãn bất phương trình 9x2−4+(x2−4).2019x−2≥1{9^{{x^2} - 4}} + \left( {{x^2} - 4} \right){.2019^{x - 2}} \ge 1 là khoảng (a;b). Tính b - a

A.  
5
B.  
4
C.  
-5
D.  
-1
Câu 41: 1 điểm

Cho hàm số f liên tục trên R và ∫01f(x)dx=6.\int\limits_0^1 {f\left( x \right)dx} = 6. Tính ∫01[xf(x2)−x2f(x3)]dx.\int\limits_0^1 {\left[ {xf\left( {{x^2}} \right) - {x^2}f\left( {{x^3}} \right)} \right]dx} .

A.  
0
B.  
1
C.  
-1
D.  
16.\frac{1}{6}.
Câu 42: 1 điểm

Có bao nhiêu số phức z thỏa mãn ∣z+1−3i∣=32\left| {z + 1 - 3i} \right| = 3\sqrt 2 và (z+2i)2{\left( {z + 2i} \right)^2} là số thuần ảo?

A.  
1
B.  
2
C.  
3
D.  
4
Câu 43: 1 điểm

Cho hình chóp S.ABCD có đáy là vuông cạnh a hình chiếu vuông góc của S lên mặt phẳng (ABCD) trùng với trung điểm của cạnh AD cạnh bên SB hợp với đáy một góc 60o. Tính theo a thể tích V của khối chóp S.ABCD.

A.  
V=a3152.V = \frac{{{a^3}\sqrt {15} }}{2}.
B.  
V=a3156.V = \frac{{{a^3}\sqrt {15} }}{6}.
C.  
V=a354.V = \frac{{{a^3}\sqrt 5 }}{4}.
D.  
V=a3563.V = \frac{{{a^3}\sqrt 5 }}{{6\sqrt 3 }}.
Câu 44: 1 điểm

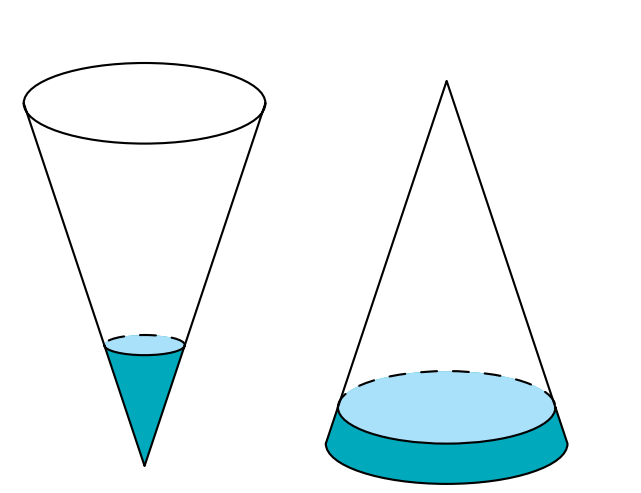
Một cái phễu có dạng hình nón. Người ta đổ một lượng nước vào phễu sao cho chiều cao của lượng nước trong phễu bằng 13\frac{1}{3} chiều cao của phễu. Hỏi nếu bịt kín miệng phễu rồi lộn ngược phễu lên thì chiều cao của mực nước xấp xỉ bằng bao nhiêu? Biết rằng chiều cao của phễu là 15 cm.

Hình ảnh

A.  
0,5cm
B.  
0,3cm
C.  
0,188cm
D.  
0,216cm
Câu 45: 1 điểm

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P):x−2y+2z−2=0\left( P \right):x-2y+2z-2=0 và điểm I(−1;2;−1)I\left( -1;2;-1 \right) . Viết phương trình mặt cầu (S)\left( S \right) có tâm I và cắt mặt phẳng (P)\left( P \right) theo giao tuyến là đường tròn có bán kính bằng 5.

A.  
(S):(x−1)2+(y+2)2+(z−1)2=34.\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z - 1} \right)^2} = 34.
B.  
(S):(x+1)2+(y−2)2+(z+1)2=16\left( S \right):{\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 16
C.  
(S):(x+1)2+(y−2)2+(z+1)2=25\left( S \right):{\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 25
D.  
(S):(x+1)2+(y−2)2+(z+1)2=34\left( S \right):{\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 34
Câu 46: 1 điểm

Cho hàm số f(x) liên tục trên R bảng biến thiên của hàm số f'(x) như sau:

Hình ảnh

Số điểm cực trị của hàm số g(x)=f(x+1x−1)g\left( x \right) = f\left( {\frac{{x + 1}}{{x - 1}}} \right) là

A.  
8
B.  
7
C.  
1
D.  
3
Câu 47: 1 điểm

Trong các nghiệm (x;y) thỏa mãn bất phương trình log⁡x2+2y2(2x+y)≥1.{\log _{{x^2} + 2{y^2}}}\left( {2x + y} \right) \ge 1. Giá trị lớn nhất của biểu thức T = 2x + y bằng

A.  
94.\frac{9}{4}.
B.  
92.\frac{9}{2}.
C.  
98.\frac{9}{8}.
D.  
9
Câu 48: 1 điểm

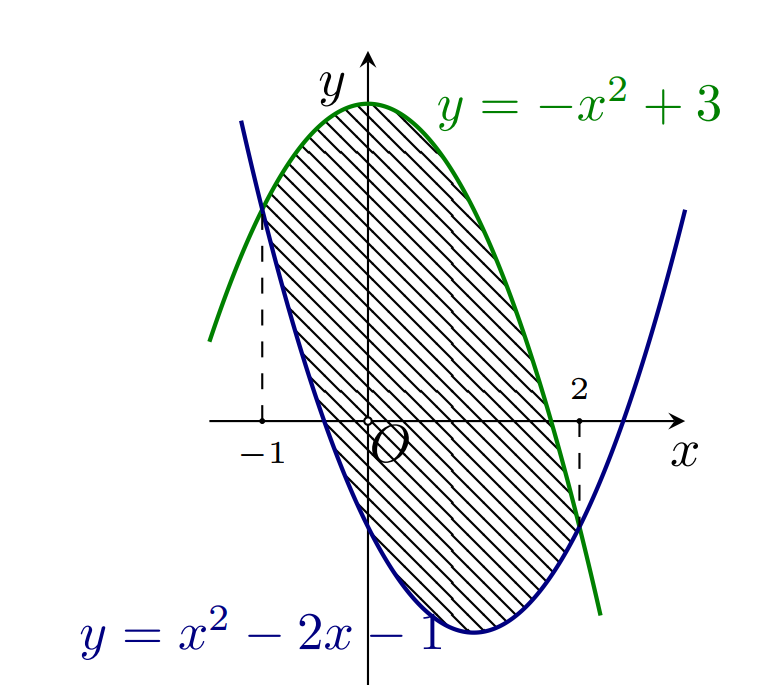
Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây?

Hình ảnh

A.  
∫−12(2x2−2x−4)dx.\int\limits_{ - 1}^2 {\left( {2{x^2} - 2x - 4} \right)dx} .
B.  
∫−12(−2x+2)dx.\int\limits_{ - 1}^2 {\left( { - 2x + 2} \right)dx.}
C.  
∫−12(2x−2)dx.\int\limits_{ - 1}^2 {\left( {2x - 2} \right)dx} .
D.  
∫−12(−2x2+2x+4)dx.\int\limits_{ - 1}^2 {\left( { - 2{x^2} + 2x + 4} \right)dx.}
Câu 49: 1 điểm

Cho số phức z thỏa mãn ∣z−3−4i∣=5.\left| z-3-4i \right|=\sqrt{5}. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P=∣z+2∣2−∣z−i∣2.P={{\left| z+2 \right|}^{2}}-{{\left| z-i \right|}^{2}}. Tính mô-đun của số phức w=M+mi.\text{w}=M+mi.

A.  
∣w∣=1258\left| {\rm{w}} \right| = \sqrt {1258}
B.  
∣w∣=3137.\left| {\rm{w}} \right| = 3\sqrt {137} .
C.  
∣w∣=2314.\left| {\rm{w}} \right| = 2\sqrt {314} .
D.  
∣w∣=2309\left| {\rm{w}} \right| = 2\sqrt {309}
Câu 50: 1 điểm

Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật, AB=a,SA vuông góc với mặt phẳng đáy và SA=a. Góc giữa hai mặt phẳng (SBC)\left( SBC \right) và (SCD)\left( SCD \right) bằng φ,\varphi , với cos⁡φ=13.\cos \varphi =\frac{1}{\sqrt{3}}. Thể tích khối chóp đã cho bằng

A.  
2a33.\frac{{2{a^3}}}{3}.
B.  
a323.\frac{{{a^3}\sqrt 2 }}{3}.
C.  
a32{a^3}\sqrt 2
D.  
22a33.\frac{{2\sqrt 2 {a^3}}}{3}.

Xem thêm đề thi tương tự

thumbnail
[2021] Trường THPT Nguyễn Văn Linh - Đề thi thử THPT QG năm 2021 môn Sinh họcTHPT Quốc giaSinh học
Đề thi thử THPT Quốc gia môn Sinh học năm 2021 từ Trường THPT Nguyễn Văn Linh. Nội dung đề thi bao gồm các chủ đề Di truyền học người, Quần xã sinh vật, và bài toán Sinh học thực tiễn, giúp học sinh tự đánh giá năng lực và chuẩn bị tốt nhất.

40 câu hỏi 1 mã đề 1 giờ

208,908 lượt xem 112,483 lượt làm bài

Chưa chinh phục!!!
thumbnail
[2021] Trường THPT Nguyễn Văn Linh lần 2 - Đề thi thử THPT QG năm 2021 môn Sinh
Chưa có mô tả

40 câu hỏi 1 mã đề 1 giờ

214,475 lượt xem 115,479 lượt làm bài

Chưa chinh phục!!!
thumbnail
[2021] Trường THPT Nguyễn Văn Linh lần 2 - Đề thi thử THPT QG năm 2021 môn Toán
Đề thi thử THPT Quốc gia môn Toán năm 2021 (lần 2) của Trường THPT Nguyễn Văn Linh, miễn phí với đáp án chi tiết. Nội dung đề thi bám sát chương trình lớp 12, bao gồm các câu hỏi từ cơ bản đến nâng cao như giải tích, xác suất và hình học không gian. Đây là tài liệu luyện thi hiệu quả giúp học sinh tự đánh giá năng lực và chuẩn bị tốt cho kỳ thi.

50 câu hỏi 1 mã đề 1 giờ

221,157 lượt xem 119,077 lượt làm bài

Chưa chinh phục!!!
thumbnail
[2021] Trường THPT Nguyễn Văn Cừ lần 2 - Đề thi thử THPT QG năm 2021 môn ToánTHPT Quốc giaToán
Đề thi thử THPT Quốc gia môn Toán năm 2021 của Trường THPT Nguyễn Văn Cừ, lần 2, miễn phí và có đáp án chi tiết. Nội dung tập trung vào các dạng bài như giải tích, hình học không gian, và số phức, hỗ trợ học sinh ôn luyện toàn diện.

50 câu hỏi 1 mã đề 1 giờ

217,426 lượt xem 117,068 lượt làm bài

Chưa chinh phục!!!
thumbnail
[2021] Trường THPT Nguyễn Văn Trỗi - Đề thi thử THPT QG năm 2021 môn Hóa học
Chưa có mô tả

40 câu hỏi 1 mã đề 1 giờ

219,424 lượt xem 118,146 lượt làm bài

Chưa chinh phục!!!
thumbnail
[2021] Trường THPT Nguyễn Văn Công - Đề thi thử THPT QG năm 2021 môn Sinh
Chưa có mô tả

40 câu hỏi 1 mã đề 1 giờ

200,745 lượt xem 108,087 lượt làm bài

Chưa chinh phục!!!
thumbnail
[2021] Trường THPT Nguyễn Văn Thìn - Đề thi thử THPT QG năm 2021 môn Sinh
Chưa có mô tả

40 câu hỏi 1 mã đề 1 giờ

199,751 lượt xem 107,555 lượt làm bài

Chưa chinh phục!!!
thumbnail
[2021] Trường THPT Nguyễn Văn Trỗi lần 2 - Đề thi thử THPT QG năm 2021 môn ToánTHPT Quốc giaToán
Đề thi thử THPT Quốc gia môn Toán năm 2021 (lần 2) từ Trường THPT Nguyễn Văn Trỗi, miễn phí với đáp án đầy đủ. Nội dung bao gồm các dạng bài quan trọng như giải tích, logarit, và bài toán thực tế, giúp học sinh rèn luyện toàn diện các kỹ năng toán học.

50 câu hỏi 1 mã đề 1 giờ

205,100 lượt xem 110,432 lượt làm bài

Chưa chinh phục!!!
thumbnail
[2021] Trường THPT Nguyễn Văn Cừ - Đề thi thử THPT QG năm 2021 môn Toán
Đề thi thử THPT Quốc gia năm 2021 môn Toán từ Trường THPT Nguyễn Văn Cừ, miễn phí với đáp án đầy đủ. Đề thi tập trung vào các dạng bài quan trọng như logarit, tích phân, số phức và hình học không gian. Đây là tài liệu luyện thi hiệu quả, giúp học sinh nâng cao kỹ năng giải toán và tự tin trước kỳ thi Quốc gia.

50 câu hỏi 1 mã đề 1 giờ

221,617 lượt xem 119,322 lượt làm bài

Chưa chinh phục!!!