[2021] Trường THPT Trần Quang Khải - Đề thi thử THPT QG năm 2021 môn Toán

Cho các số nguyên k, n thỏa $0 < k \le n$ . Công thức nào dưới đây đúng?

Cho cấp số cộng (u_n) với u₁ = 2 và công sai d = 1. Khi đó u₃ bằng

Phương trình 2^x = 0,5 có một nghiệm là

Thể tích khối lăng trụ có chiều cao h và diện tích đáy bằng B là.

Cho hàm số $f\left( x \right) = 4{x^3} + 2x + 1$ . Tìm $\int {f\left( x \right){\rm{d}}x}$ .

Cho hình chóp S.ABC có SA, SB, S đôi một vuông góc với nhau và $SA = 2\sqrt 3$ , SB = 2, SC = 3. Tính thể tích khối chóp S.ABC.

Cho khối nón có bán kính đáy $r = \sqrt 3$ và chiều cao h = 4. Tính thể tích V của khối nón đã cho.

Diện tích của mặt cầu bán kính R là

Diện tích xung quanh của hình trụ có bán kính đáy R = 2 và đường sinh l = 3 bằng:

Đồ thị hàm số nào dưới đây có tâm đối xứng là điểm I(1;-2)?

Tìm phương trình tiệm cận đứng của đồ thị hàm số $y = \frac{{x - 1}}{{x + 1}}$ .

Tìm tập xác định S của bất phương trình 3^-3x > 3^-x+2

Cho hàm số $y = - {x^3} + 2{x^2}$ có đồ thị (C). Có bao nhiêu tiếp tuyến của đồ thị (C) song song với đường thẳng y = x.

Nếu $\int\limits_a^d {f(x)} dx = 5$ và $\int\limits_d^b {f(x)} dx = 2$ (a < d < b). Tích phân $\int\limits_a^b {f(x)} dx$ bằng

Cho số phức z = 3 + i. Tính $\left| {\overline z } \right|$

Cho hai số phức ${z_1} = 2 + 3i,{z_2} = - 4 - 5i$ . Tính $z = {z_1} + {z_2}$

Hỏi điểm M(3;-1) là điểm biểu diễn số phức nào sau đây ?

Trong không gian với hệ tọa độ Oxyz, cho điểm K(2;4;6), gọi K' là hình chiếu vuông góc của K lên Oz, khi đó trung điểm của OK' có tọa độ là:

Trong không gian Oxyz, cho mặt cầu (P) có phương trình ${x^2} + {y^2} + {z^2} - 2x - 4y - 6z - 11 = 0$ . Tọa độ tâm T của (P) là.

Trong không gian hệ tọa độ Oxyz, mặt phẳng $\left( \alpha \right):x - 2y + 3z + 2018 = 0$ có một véctơ pháp tuyến là

Trong không gian với hệ trục tọa độ Oxyz, cho hai mặt phẳng $\left( P \right):x + y - z + 1 = 0$ và $\left( Q \right):2x - y + z - 3 = 0$ cắt nhau theo giao tuyến là đường thẳng $\left( \Delta \right)$ . Một véc tơ chỉ phương của $\left( \Delta \right)$ có tọa độ là

Trong các mệnh đề sau, mệnh đề nào sai?

Tìm tất cả các giá trị tham số m để đồ thị hàm số $y = \frac{{mx + 1}}{{x - m}}$ đi qua A(1;-3).

Cho hình nón có độ dài đường sinh bằng 2a và chu vi đáy bằng $2\pi a$ . Tính diện tích xung quanh S của hình nón.

Cho hàm số y = f(x) là hàm số chẵn, liên tục trên R và số thực a dương thỏa $\int\limits_0^a {f\left( x \right){\rm{d}}x = 3}$ . Tính $I = \int\limits_{ - a}^a {\left( {f\left( x \right) - x} \right){\rm{d}}x}$ .

Tính diện tích hình phẳng được giới hạn bởi hai đồ thị $y = - {x^2} + 2{\rm{x}} + 1$ ; $y = 2{{\rm{x}}^2} - 4{\rm{x}} + 1$ .

Cho số phức z thỏa mãn điều kiện $\left( {1 + i} \right)\bar z - 1 - 3i = 0$ . Tìm phần ảo của số phức $w = 1 - zi + \bar z$ .

Gọi z₀ là nghiệm phức có phần ảo âm của phương trình $2{z^2} - 6z + 5 = 0$ . Tìm $i{z_0}$ ?

Trong không gian hệ tọa độ Oxyz, cho điểm A(1;-1;2). Phương trình mặt phẳng (Q) đi qua các hình chiếu của điểm A trên các trục tọa độ là

Trong không gian Oxyz, phương trình nào dưới đây khôngphải là phương trình đường thẳng đi qua hai điểm A(4;2;0), B(2;3;1).

Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B; $AB = BC = \frac{1}{2}AD = a$ . Biết SA vuông góc với mặt phẳng đáy, $SA = a\sqrt 2$ . Tính theo a khoảng cách d từ B đến mặt phẳng (SCD).

Có 25 học sinh được chia thành 2 nhóm A và B, sao cho trong mỗi nhóm đều có nam và nữ. Chọn ngẫu nhiên từ mỗi nhóm một học sinh. Tính xác suất để hai học sinh được chọn có cả nam và nữ. Biết rằng xác suất chọn được hai học sinh nam là 0,57.

Có bao nhiêu giá trị nguyên của tham số m để phương trình $\frac{3}{4}{\cos ^2}2x + 3\sin x.\cos x - \frac{m}{4} + \frac{9}{4} = 0$ có nghiệm?

Biết $A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right)$ là hai điểm thuộc hai nhánh khác nhau của đồ thị hàm số $y = \frac{{x + 4}}{{x + 1}}$ sao cho độ dài đoạn thẳng AB nhỏ nhất. Tính $P = y_A^2 + y_B^2 - {x_A}{x_B}$ .

Cho hình lăng trụ đều ABC.A'B'C', biết góc giữa hai mặt phẳng (A'BC) và (ABC) bằng 45^o, diện tích tam giác A'BC bằng ${a^2}\sqrt 6$ . Tính diện tích xung quanh của hình trụ ngoại tiếp hình lăng trụ ABC.A'B'C'.

Cho hàm số f(x) có đạo hàm liên tục trên đoạn [0;1] thỏa mãn $f\left( 1 \right) = 1,\,\int\limits_0^1 {{{\left[ {f'\left( x \right)} \right]}^2}{\rm{d}}x = \frac{9}{5}}$ và $\int\limits_0^1 {f\left( {\sqrt x } \right){\rm{d}}x} = \frac{2}{5}$ . Tính tích phân $I = \int\limits_0^1 {f\left( x \right){\rm{d}}x}$ .

Cho số thực a > 1. Gọi A, B, C lần lượt là các điểm thuộc đồ thị các hàm số $y = {a^x};\,y = {\left( {\frac{1}{a}} \right)^x};y = {\log _{\frac{1}{a}}}x.$ Biết tam giác ABC vuông cân đỉnh A, AB = 4 và đường thẳng AC song song với trục Oy. Khi đó giá trị a bằng:

Xếp ngẫu nhiên 4 bạn nam và 5 bạn nữ ngồi vào 9 cái ghế kê theo một hàng ngang. Xác suất để có được 5 bạn nữ ngồi cạnh nhau là:

Cho lăng trụ đứng tam giác ABC.A'B'C' có đáy là một tam giác vuông cân tại B, AB = BC = a, $AA' = a\sqrt 2$ , M là trung điểm BC. Tính khoảng cách giữa hai đường thẳng AM và B'C.

Có bao nhiêu giá trị nguyên của tham số m sao cho hàm số $y = \frac{{{x^3}}}{3} + m{x^2} - mx - m$ đồng biến trên R?

Số lượng một loại vi rút cúm mùa chủng A(vi rút A) trong phòng thí nghiệm được tính theo công thức $s\left( t \right) = s\left( 0 \right){.2^t},$ trong đó s(0) là số lượng vi rút A lúc ban đầu, s(t) là số lượng vi rút A sau t giờ. Biết sau 3 giờ thì số lượng vi rút A là 625 nghìn con và nếu số lượng vi rút lớn hơn $2,{1.10^{19}}$ thì người nhiễm vi rút A sẽ có biểu hiện sốt và đau họng. Hỏi sau ít nhất bao nhiêu ngày kể từ khi bắt đầu nhiễm thì bệnh nhân sẽ có biểu hiện sốt và đau họng?

Một khối trụ có bán kính đáy r = 5a và thể tích bằng $V = 175\pi {a^3}$ . Cắt khối trụ bởi một mặt phẳng song song với trục và cách trục 3a. Diện tích của thiết diện được tạo nên bằng

Cho x, y là các số thực dương thỏa mãn $\ln \frac{{\sqrt {1 + xy} }}{{x + y}} = \frac{{{x^2} + {y^2} + xy - 1}}{2}$ . Biết giá trị lớn nhất của của biểu thức $P = \frac{{xy}}{{x + y}}$ bằng $\frac{{\sqrt a }}{b}$ trong đó a là số nguyên tố. Tính ab²

Cho hàm số $f\left( x \right) = \frac{{2x - m}}{{x + 2}}$ (m là tham số thực). Gọi S là tập hợp tất cả các giá trị của m sao cho $\mathop {\max }\limits_{\left[ {0;2} \right]} \left| {f\left( x \right)} \right| + \mathop {\min }\limits_{\left[ {0;2} \right]} \left| {f\left( x \right)} \right| = 4$ . Số phần tử của S là

Cho khối tứ diện ABCD có thể tích 2020. Gọi M, N, P, Q lần lượt là trọng tâm của các tam giác ABC, ABD, ACD, BCD. Tính theo V thể tích của khối tứ diện MNPQ.

Cho x, y, z là các số thực không âm thỏa ${2^x} + {2^y} + {2^z} = 4$ . Giá trị nhỏ nhất của biểu thức P = x +y + z?

Cho hàm số $y = \frac{{ax + b}}{{cx + d}};\left( {a,b,c,d \in R} \right)$ có bảng biến thiên như sau:

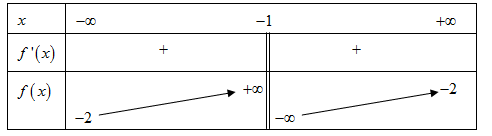
Mệnh đề nào dưới đây đúng?

Cho hàm số f(x) có bảng biến thiên như sau:

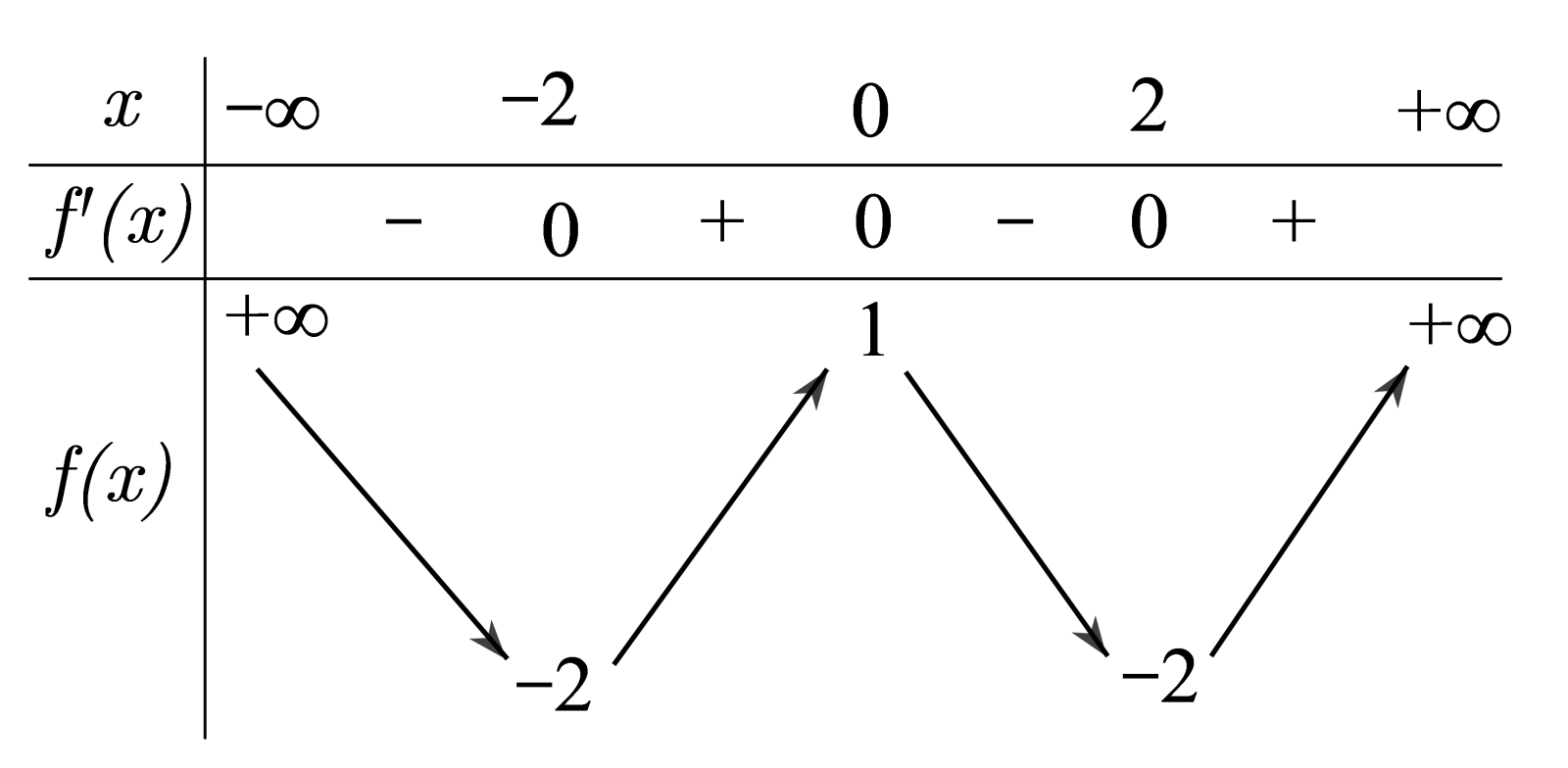
Số nghiệm thuộc đoạn $\left[ {0;\frac{{7\pi }}{2}} \right]$ của phương trình $f\left( {2\cos x} \right) = \frac{1}{2}$ là

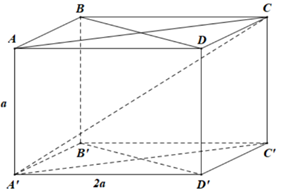
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = AA' = a,AD = 2a. Gọi góc giữa đường chéo A'C và mặt phẳng đáy (ABCD) là $\alpha$ . Khi đó $\tan \alpha$ bằng

Cho hàm số f(x), bảng xét dấu f'(x) của như sau:

Số điểm cực trị của hàm số đã cho là