[2021] Trường THPT Trần Văn Giàu lần 2 - Đề thi thử THPT QG năm 2021 môn Toán

Một lớp học có 25 học sinh nam và 17 học sinh nữ. Hỏi có bao nhiêu cách chọn ra một học sinh nam và một học sinh nữ trong lớp học này đi dự trại hè của trường?

Cho cấp số nhân $\left( {{u}_{n}} \right)$ , biết ${{u}_{1}}=3;\,q=-2$ . Tìm ${{u}_{5}}$ .

Cho hàm bậc ba $y=f\left( x \right)$ có đồ thị trong hình bên.

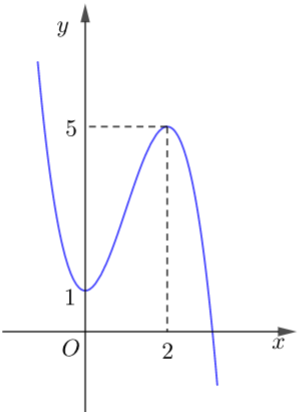
Hàm số đã cho đồng biến trên khoảng nào?

Cho hàm số $f\left( x \right)$ có bảng biến thiên như sau:

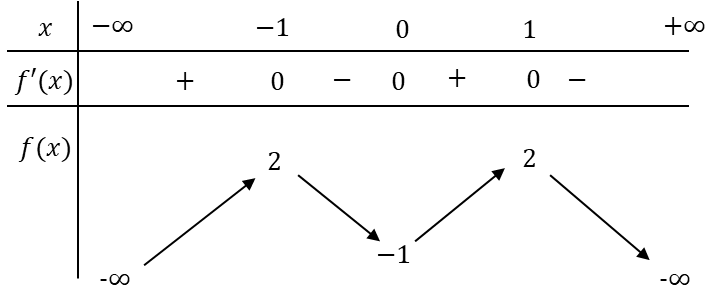
Hàm số đạt cực tiểu tại

Cho hàm số $f\left( x \right)$ liên tục trên $\mathbb{R}$ , bảng xét dấu của ${f}'\left( x \right)$ như sau:

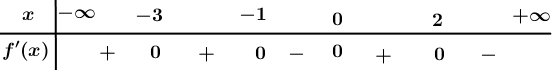
Hàm số đã cho có mấy điểm cực trị?

Tiệm cận ngang của đồ thị hàm số $y = \frac{{3x - 5}}{{4x - 8}}$ là

Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên?

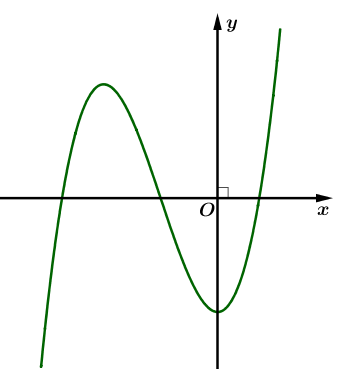
Xác định số giao điểm của đồ thị hàm số $y={{x}^{4}}-4{{x}^{2}}-5$ với trục hoành.

Với a là số thực dương tùy ý, ${{\log }_{4}}\left( {{a}^{2022}} \right)$ bằng

Đạo hàm của hàm số $y = {\log _5}x$ là

Rút gọn biểu thức $N = {x^{\frac{1}{2}}}\sqrt[6]{x}$ với x > 0

Tìm nghiệm của phương trình ${3^{x - 2}} = 27$

Nghiệm của phương trình ${\log _2}\left( {4x - 3} \right) = 2$ là

Họ tất cả các nguyên hàm của hàm số $f\left( x \right)=4x+\sin x$ là

Hàm số $f\left( x \right)=\cos \left( 4x+5 \right)$ có một nguyên hàm là

Cho các hàm số $f\left( x \right)$ và $F\left( x \right)$ liên tục trên $\mathbb{R}$ thỏa ${F}'\left( x \right)=f\left( x \right),\forall x\in \mathbb{R}.$ . Tính $\int\limits_{0}^{1}{f\left( x \right)\text{d}x}$ biết $F\left( 0 \right)=2,F\left( 1 \right)=6$ .

Tích phân $\int\limits_1^2 {2{x^4}} {\rm{d}}x$ bằng

Cho số phức z có điểm biểu diễn trong mặt phẳng tọa độ Oxy là điểm $M\left( 3;-5 \right)$ . Xác định số phức liên hợp $\bar{z}$ của z.

Cho hai số phức ${{z}_{1}}=3-7i$ và ${{z}_{2}}=2+3i$ . Tìm số phức $z={{z}_{1}}+{{z}_{2}}$ .

Điểm biểu diễn hình học của số phức z=2-3i là điểm nào trong các điểm sau đây?

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA=3a và SA vuông góc với mặt phẳng đáy. Tính thể tích khối chóp S.ABCD.

Cho khối lập phương $ABCD.{A}'{B}'{C}'{D}'$ có đường chéo $A{C}'$ bằng $a\sqrt{3},(a>0).$ Thể tích của khối lập phương đã cho bằng

Diện tích S của mặt cầu có bán kính đáy r bằng

Cho hình trụ có bán kính đường tròn đáy $r=5\text{cm}$ và có chiều cao $h=10\text{cm}$ . Diện tích xung quanh của hình trụ bằng

Trong không gian Oxyz, cho điểm $I\left( -5;0;5 \right)$ là trung điểm của đoạn MN, biết $M\left( 1;-4;7 \right)$ . Tìm tọa độ của điểm N.

Trong không gian Oxyz, cho mặt cầu $\left( S \right):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-2x+4y-6z+3=0$ . Tâm của $\left( S \right)$ có tọa độ là

Xác định m để mặt phẳng (P):3x-4y+2z+m=0 đi qua điểm A(3;1;-2).

Trong không gian Oxyz, vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng đi qua hai điểm $A\left( 0;4;3 \right)$ và $B\left( 3;-2;0 \right)$ ?

Một hộp đựng thẻ được đánh số từ 1, 2, 3,…, 9. Rút ngẫu nhiên hai lần, mỗi lần một thẻ và nhân số ghi trên hai thẻ với nhau. Xác suất để tích nhận được là số chẵn là

Hàm số nào dưới đây đồng biến trên khoảng $\left( -\infty ;+\infty \right)$ ?

Giá trị lớn nhất của hàm số $y = \sqrt {4 - {x^2}}$ là

Tập nghiệm của bất phương trình ${\left( {\frac{{\rm{e}}}{\pi }} \right)^x} > 1$ là

Nếu ${\log _7}x = 8{\log _7}a{b^2} - 2{\log _7}{a^3}b\,\,(a,b > 0)$ thì $x$ bằng :

Tính môđun của số phức z biết $\bar{z}=\left( 4-3i \right)\left( 1+i \right)$ .

Cho hình lăng trụ đứng $ABC.{A}'{B}'{C}'$ có đáy ABC là tam giác vuông tại B, AB=BC=a, $BB'=a\sqrt{3}$ . Tính góc giữa đường thẳng ${A}'B$ và mặt phẳng $\left( BC{C}'{B}' \right)$ .

Cho hình chóp S.ABC có đáy là tam giác vuông cân tại C,BC=a, SA vuông góc với mặt phẳng đáy và SA=a. Khoảng cách từ A đến mặt phẳng $\left( SBC \right)$ bằng

Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt cầu có tâm $I\left( 1\,;\,-4\,;\,3 \right)$ và đi qua điểm $A\left( 5\,;\,-3\,;\,2 \right)$ .

Phương trình trung tuyến AM của tam giác ABC với $A(3;1;2),\,B(-3;2;5),C(1;6;-3)$ là

Cho hàm số $y=f\left( x \right)$ . Đồ thị hàm $y={f}'\left( x \right)$ như hình vẽ

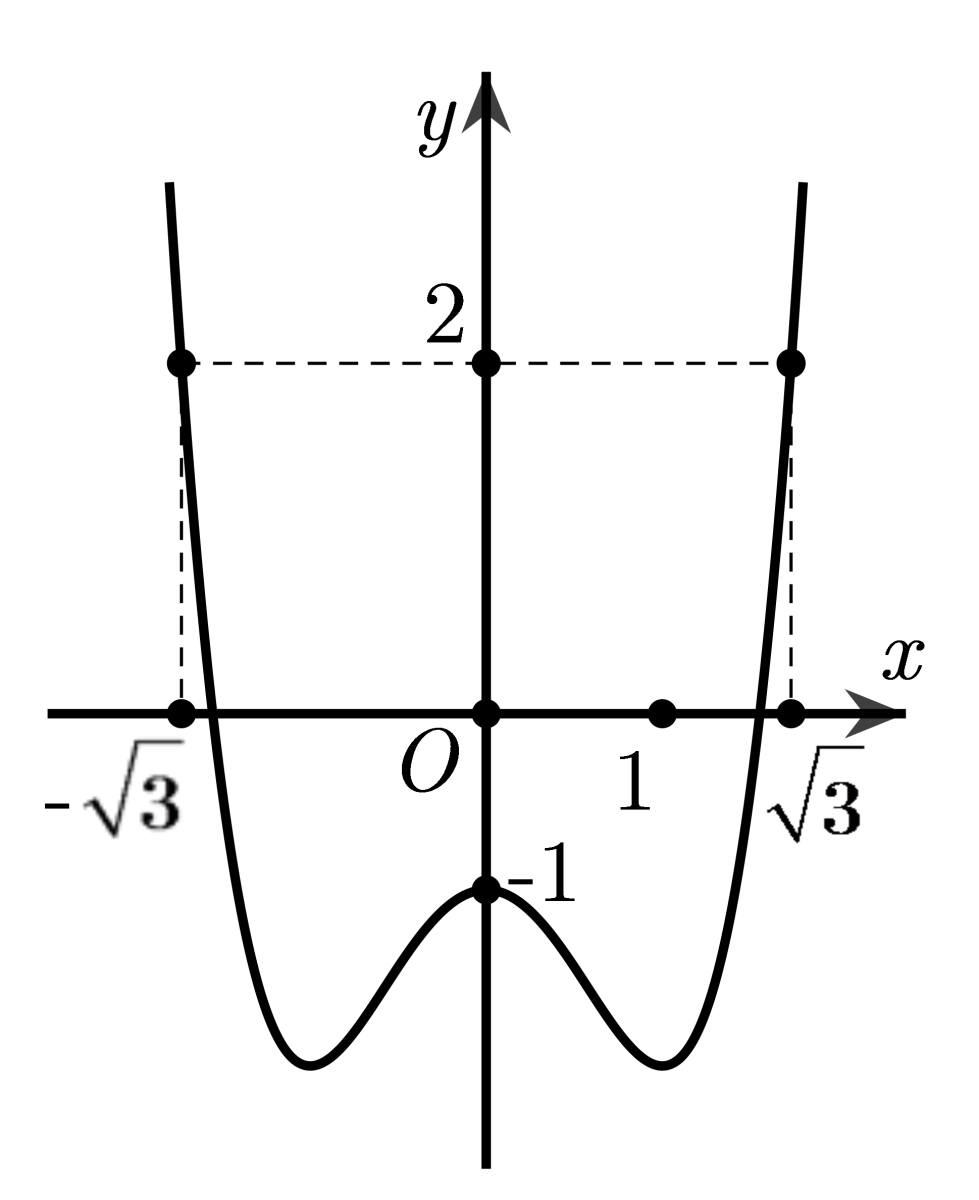
Đặt $h\left( x \right)=3f\left( x \right)-{{x}^{3}}+3x$ . Tìm mệnh đề đúng trong các mệnh đề sau:

Tập nghiệm của bất phương trình $({{3}^{2x}}-9)({{3}^{x}}-\frac{1}{27})\sqrt{{{3}^{x+1}}-1}\le 0$ chứa bao nhiêu số nguyên ?

Cho hàm số $f\left( x \right) = x + \sqrt {{x^2} + 1}$ biết $\int\limits_0^1 {\frac{{f\left( x \right)}}{{f\left( { - x} \right)}}} {\rm{d}}x = a + b\sqrt c$ với $a,\,b,\,c$ là các số hữu tỷ tối giãn . Tính P = a + b + c

Có bao nhiêu số phức z thỏa mãn $\left| \overline{z}-2i \right|=3$ và $\left( zi-4i+5 \right)3i$ là số thực ? .

Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, đường thẳng SO vuông góc với mặt phẳng $\left( ABCD \right)$ . Biết $AB=SB=a\sqrt{2}, SO=a$ . Tính tan của góc giữa hai mặt phẳng $\left( SAB \right)$ và $\left( SAD \right).$

Viết các số theo thứ tự tăng dần: ${\left( {{1 \over 3}} \right)^0}\,,\,\,{\left( {{1 \over 3}} \right)^{ - 1}},\,\,{\left( {{1 \over 3}} \right)^\pi },\,\,{\left( {{1 \over 3}} \right)^{\sqrt 2 }}$ .

Trong không gian với hệ toạ độ Oxyz, cho hai đường thẳng ${{\Delta }_{1}}:\,\frac{x}{1}=\frac{y-4}{2}=\frac{z-1}{3}$ và ${{\Delta }_{2}}:\,\frac{x+2}{-1}=\frac{y}{-2}=\frac{z-1}{3}$ cắt nhau và cùng nằm trong mặt phẳng $\left( P \right)$ . Đường phân giác d của góc nhọn tạo bởi ${{\Delta }_{1}}, {{\Delta }_{2}}$ và nằm trong mặt phẳng $\left( P \right)$ có một véctơ chỉ phương là

Cho hàm số $f(x)={{x}^{3}}-3{{x}^{2}}+1$ và $g(x)=f\left( \left| f(x) \right|-m \right)$ cùng với x=-1, x=1 là hai điểm cực trị trong nhiều điểm cực trị của hàm số y=g(x). Khi đó số điểm cực trị của hàm y=g(x) là

Biết rằng có n cặp số dương $\left( x;y \right)$ ( với n bất kỳ) để $x;\,{{x}^{\log \left( x \right)}};{{y}^{\log \left( y \right)}};\,x{{y}^{\log \left( xy \right)}}$ tạo thành 1 cấp số nhân. Vậy giá trị gần nhất của biểu thức $\frac{\sum\limits_{k=1}^{n}{{{x}_{n}}}}{\sum\limits_{k=1}^{n}{{{y}_{n}}}}$ nằm trong khoảng nào ?

Cho hàm số $y={{x}^{2}}$ có đồ thị $\left( C \right)$ , biết rằng tồn tại hai điểm A, B thuộc đồ thị $\left( C \right)$ sao cho tiếp tuyến tại A, B và đường thẳng pháp tuyến của hai tiếp tuyến đó tạo thành một hình chữ nhật có chiều dài gấp đôi chiều rộng. Gọi ${{S}_{1}}$ là diện tích giới hạn bởi đồ thị $\left( C \right)$ và hai tiếp tuyến, $S{{}_{2}}$ là diện tích hình chữ nhật giới hạn bởi các tiếp tuyến và pháp tuyến tại A,B. Tính tỉ số $\frac{{{S}_{1}}}{{{S}_{2}}}$ ?

Trong không gian Oxyz, cho hai điểm $A\left( 0;1;2 \right)$ và $B\left( \sqrt{3};1;3 \right)$ thoả mãn $AB\bot BC,AB\bot AD, AD\bot BC$ . Gọi (S) là mặt cầu có đường kính AB, đường thẳng CD di động và luôn tiếp xúc với mặt cầu (S). Gọi $E\in AB,F\in CD$ và EF là đoạn vuông góc chung của AB và CD. Biết rằng đường thẳng $(\Delta )\bot EF;(\Delta )\bot AB$ và $d\left( A;\left( \Delta \right) \right)=\sqrt{3}$ . Khoảng cách giữa $\Delta$ và CD lớn nhất bằng

Cho số phức z thỏa $\left| {{z}_{1}}+1 \right|+\left| {{z}_{1}}-1 \right|+\left| {{z}_{1}}-\overline{{{z}_{1}}}-4 \right|\le 6$ và $\left| {{z}_{2}}-5i \right|\le 2$ thì giá trị nhỏ nhất của $\left| {{z}_{1}}-{{z}_{2}} \right|=m$ . Khẳng định đúng là