[2022] Trường THPT Cần Thạnh - Đề thi thử THPT QG năm 2022 môn Toán

Hãy tìm $\int {\dfrac{{5x + 1}}{{{x^2} - 6x + 9}}\,dx}$ .

Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường $y = \tan x,\,\,y = 0,\,\,x = \dfrac{\pi }{3}$ quanh Ox là:

Giá trị nhỏ nhất của hàm số $y = {x^3} - 3x + 5$ trên đoạn [2 ; 4] là:

Cho hàm số $y = a{x^3} + b{x^2} + cx + d\,\,\,(a,b,c,d\, \in R)$ có đồ thị như hình vẽ sau.

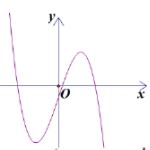
Số điểm cực trị của hàm số đã cho là:

Tập nghiệm của bất phương trình ${\left( {{{\log }_2}x} \right)^2} - 4{\log _2}x + 3 > 0$ là:

Cho hàm số $y = {2^x} - 2x$ . Khẳng định nào sau đây sai :

Số đỉnh của một hình bát diện đều là:

Khối chóp có diện tích đáy 4 $m^2$ và chiều cao 1,5m có thể tích là:

Một hình trụ có bán kính đáy r = 5 cm và khoảng cách giữa hai đáy bằng 7cm. Khi đó diện tích xung quanh của hình trụ là:

Trong không gian cho hai điểm $A\left( { - 1;2;3} \right),\,B\left( {0;1;1} \right)$ , độ dài đoạn $AB$ bằng

Cho các số phức ${z_1} = 2 - 5i\,,\,\,{z_2} = - 2 - 3i$ . Hãy tính $|{z_1} - {z_2}|$ .

Cho số phức z thỏa mãn $\left( {3 - 2i} \right)z = 4 + 2i$ . Tìm số phức liên hợp của z.

Cho hàm số y = f(x) có bảng biến thiên như dưới đây.

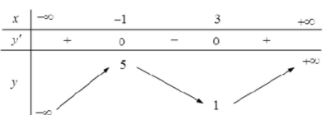
Đồ thị của hàm số y = |f(x)| có bao nhiêu điểm cực trị ?

Cho hàm số y = f(x) có bảng biến thiên như sau:

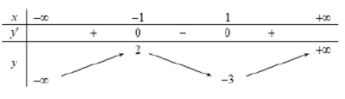
Số nghiệm của phương trình f(x) +3 = 0 là:

Đường thẳng $y = 2x - 1$ có bao nhiêu điểm chung với đồ thị hàm số $y = {{{x^2} - x - 1} \over {x + 1}}$ .

Tìm $I = \int {\cos \left( {4x + 3} \right)\,dx}$ .

Đặt $F(x) = \int\limits_1^x {t\,dt}$ . Khi đó F’(x) là hàm số nào dưới đây ?

Giải phương trình ${z^2} - 6z + 11 = 0$ , ta có nghiệm là:

Cho z = 1 + 2i. Phần thực và phần ảo của số phức $w = 2z + \overline z$ là:

Khối chóp tứ giác đều có thể tích $V = 2{{\rm{a}}^3}$ , cạnh đáy bằng $a\sqrt 6$ thì chiều cao khối chóp bằng:

Cho khối chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$ . Hai mặt bên $\left( {SAB} \right)$ và $\left( {SAC} \right)$ cùng vuông góc với đáy. Tính thể tích khối chóp biết $SC = a\sqrt 3$

Cho hình lập phương ABCD. A'B'C'D'. Gọi (H) là hình cầu nội tiếp hình lập phương đó. Khi đó $\dfrac{{{V_{(H)}}}}{{{V_{ABCD.A'B'C'D'}}}}$ bằng:

Cho 3 điểm $M(0;1;0),N(0;2; - 4),P(2;4;0)$ . Nếu $MNPQ$ là hình bình hành thì tọa độ của điểm $Q$ là

Đạo hàm của hàm số $y = {\log _3}\left( {1 + \sqrt x } \right)$ là:

Cho x, y là hai số thực dương và m, n là hai số thực tùy ý. Đẳng thức nào sau đây sai ?

Nghiệm của hệ phương trình $\left\{ \begin{array}{l}x + 2y = 1 + i\\3x + iy = 2 - 3i\end{array} \right.$ là:

Tìm số phức có phần thực bằng 12 và mô đun bằng 13.

Trong không gian tọa độ $Oxyz$ cho ba điểm $M\left( {1;1;1} \right),\,N\left( {2;3;4} \right),\,P\left( {7;7;5} \right)$ . Để tứ giác $MNPQ$ là hình bình hành thì tọa độ điểm $Q$ là

Cho 3 điểm $A(1;1;1),B(1; - 1;0),C(0; - 2;3)$ . Tam giác $ABC$ là

Giá trị của tham sô m để phương trình ${x^3} - 3x = 2m + 1$ có ba nghiệm phân biệt là:

Trên đồ thị (C) của hàm số $y = {{x + 10} \over {x + 1}}$ có bao nhiêu điểm có tọa độ nguyên ?

Hàm số nào dưới đây không là nguyên hàm của $f(x) = \dfrac{{2x\left( {x + 3} \right)}}{{{{\left( {x + 1} \right)}^2}}}$ ?

Tính nguyên hàm $\int {{{\left( {5x + 3} \right)}^3}\,dx}$ ta được:

Cho hình chóp SABC có đáy ABC là tam giác đều cạnh a biết SA vuông góc với đáy ABC và (SBC) hợp với đáy (ABC) một góc $60^o$ . Tính thể tích hình chóp

Cho khối chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật $AD = 2a,\,AB = a$ . Gọi $H$ là trung điểm của $AD$ , biết $SH \bot \left( {ABCD} \right)$ . Tính thể tích khối chóp biết $SA = a\sqrt 5$ .

Cho hình lập phương ABCD.A'B'C'D'. Gọi (H) là hình nón tròn xoay nội tiếp hình lập phương đó. Khi đó $\dfrac{{{V_{(H)}}}}{{{V_{ABCD.A'B'C'D'}}}}$ bằng:

Trong không gian tọa độ $Oxyz$ cho ba điểm $A\left( { - 1;2;2} \right),\,B\left( {0;1;3} \right),\,C\left( { - 3;4;0} \right)$ . Để tứ giác $ABCD$ là hình bình hành thì tọa độ điểm $D$ là

Phương trình ${z^2} - 2z + 3 = 0$ có các nghiệm là:

Mô đun của tổng hai số phức ${z_1} = 3 - 4i\,,\,\,{z_2} = 4 + 3i$ :

Cho hình chóp tứ giác có đáy là hình chữ nhật cạnh các cạnh bên có độ dài bằng nhau và bằng . Thể tích khối chóp bằng:

Cho tứ diện ABCD có AD⊥(ABC) và BD⊥BC. Khi quay tứ điện đó xung quanh trục là cạnh AB, có bao nhiêu hình nón được tạo thành.

Cho hàm số $y = {{x + 3} \over {1 - x}}$ . Mệnh đề nào sau đây sai ?

Tập nghiệm của bất phương trình ${\log _{{1 \over 2}}}(2x - 2) > {\log _{{1 \over 2}}}(x + 1)$ là:

Nghiệm của phương trình ${\log _2}({\log _4}x) = 1$ là:

Cho $f(x) \ge g(x),\forall x \in [a;b]$ . Hình phẳng S₁ giới hạn bởi đường y = f(x), y = 0, x = a, x = b (a<b) đem quay quanh Ox có thể tích V₁. Hình phẳng S₂ giới hạn bởi đường y = g(x), y = 0, x = a, x = b đem quay quanh Ox có thể tích V₂. Lựa chọn phương án đúng.

Diện tích hình phẳng giới hạn bởi các đường : $y = {x^2}\,,\,y = \dfrac{{{x^2}}}{8},\,\,y = \dfrac{{27}}{x}$ là:

Chọn phương án đúng.

Cho điểm $M\left( {1;2; - 3} \right)$ , khoảng cách từ điểm $M$ đến mặt phẳng $\left( {Oxy} \right)$ bằng