Trang chủ Đề thi [2022] Trường THPT Nghi Xuân - Đề thi thử THPT QG năm 2022 môn Toán
thumbnail

[2022] Trường THPT Nghi Xuân - Đề thi thử THPT QG năm 2022 môn Toán

Thời gian làm bài: 1 giờ

Đề thi nằm trong bộ sưu tập: 📘 Tuyển Tập Bộ 500 Đề Thi Ôn Luyện Môn Toán THPT Quốc Gia Các Tỉnh Từ Năm 2018-2025 - Có Đáp Án Chi Tiết


Bạn chưa làm đề thi này!!!

Hãy bắt đầu chinh phục nào!



 

Xem trước nội dung:

Câu 1: 1 điểm

Cho hình chóp S.ABCDS.ABCD có đáy ABCDABCD là hình chữ nhật, SB⊥(ABCD),   SB=aSB \bot \left( {ABCD} \right),\,\,\,SB = a và BC=a3.BC = a\sqrt 3 . Khoảng cách giữa hai đường thẳng SDSD và ABAB bằng

A.  
a3a\sqrt 3
B.  
a22\dfrac{{a\sqrt 2 }}{2}
C.  
a32\dfrac{{a\sqrt 3 }}{2}
D.  
aa
Câu 2: 1 điểm

Hàm số f(x)=x44−2x2+6f(x) = \dfrac{{{x^4}}}{4} - 2{x^2} + 6 có bao nhiêu điểm cực đại ?

A.  
1
B.  
0
C.  
3
D.  
2
Câu 3: 1 điểm

Tính đạo hàm của hàm số f(x)=x(x−1)(x−2)...(x−2018)f\left( x \right) = x\left( {x - 1} \right)\left( {x - 2} \right)...\left( {x - 2018} \right) tại điểm x=0x = 0 .

A.  
f′(0)=0.f'\left( 0 \right) = 0.
B.  
f′(0)=−2018!.f'\left( 0 \right) = - 2018!.
C.  
f′(0)=2018!.f'\left( 0 \right) = 2018!.
D.  
f′(0)=2018.f'\left( 0 \right) = 2018.
Câu 4: 1 điểm

Cho tam giác ABC vuông cân tại A có BC =2. Tính tích vô hướng AB→.CA→\overrightarrow {AB} .\overrightarrow {CA} :

A.  
0
B.  
-4
C.  
2
D.  
4
Câu 5: 1 điểm

Cho hình vuông ABCDABCD tâm OO cạnh aa . Biết rằng tập hợp các điểm MM thỏa mãn 2MA2+MB2+2MC2+MD2=9a22M{A^2} + M{B^2} + 2M{C^2} + M{D^2} = 9{a^2} là một đường tròn. Bán kính của đường tròn đó là:

A.  
R=2aR = 2a .
B.  
R=aR = a .
C.  
R=a2R = a\sqrt 2 .
D.  
R=3aR = 3a .
Câu 6: 1 điểm

Đồ thị hình bên là của hàm số nào?

A.  
y=x3−3x+1.y = {x^3} - 3x + 1.
B.  
y=x3+3x+1.y = {x^3} + 3x + 1.
C.  
y=−x3+3x+1.y = - {x^3} + 3x + 1.
D.  
y=x3−3x2−1.y = {x^3} - 3{x^2} - 1.
Câu 7: 1 điểm

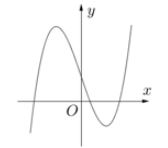
Có 5 học sinh lớp 12A1, 3 học sinh lớp 12A2, 2 học sinh lớp 12D1. Xếp ngẫu nhiên 10 học sinh trên thành một hàng dài. Tính xác suất để trong 10 học sinh trên không có hai học sinh cùng lớp đứng cạnh nhau.

A.  
13630\dfrac{{13}}{{630}}
B.  
13360\dfrac{{13}}{{360}}
C.  
11630\dfrac{{11}}{{630}}
D.  
11360\dfrac{{11}}{{360}}
Câu 8: 1 điểm

Cho hàm số y=f(x).y = f\left( x \right). liên tục trên R. Hàm số y=f′(x)y = f'\left( x \right) có đồ thị như hình vẽ bên. Hàm số y=f(x2)y = f\left( {{x^2}} \right) đồng biến trên khoảng nào dưới đây?

A.  
(−12;12).\left( { - \dfrac{1}{2};\dfrac{1}{2}} \right).
B.  
(−1;0).\left( { - 1;0} \right).
C.  
(−2;−1).\left( { - 2; - 1} \right).
D.  
(0;2).\left( {0;2} \right).
Câu 9: 1 điểm

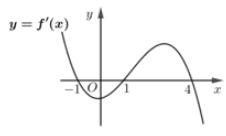
Tính lim⁡x→+∞1+3x2x2+3\mathop {\lim }\limits_{x \to + \infty } \dfrac{{1 + 3x}}{{\sqrt {2{x^2} + 3} }}

A.  
22\dfrac{{\sqrt 2 }}{2} .
B.  
−322 - \dfrac{{3\sqrt 2 }}{2}
C.  
−22 - \dfrac{{\sqrt 2 }}{2}
D.  
322\dfrac{{3\sqrt 2 }}{2}
Câu 10: 1 điểm

Đồ thị sau đây là của hàm số nào?

A.  
y=2x+1x+1y = \dfrac{{2x + 1}}{{x + 1}} .
B.  
y=x−1x+1y = \dfrac{{x - 1}}{{x + 1}} .
C.  
y=x+2x+1y = \dfrac{{x + 2}}{{x + 1}} .
D.  
x+31−x\dfrac{{x + 3}}{{1 - x}} .
Câu 11: 1 điểm

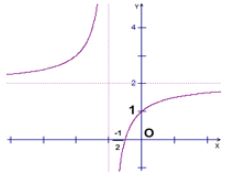
Tìm tập xác định D{\rm{D}} của hàm số y=2018sin⁡x.y = \dfrac{{2018}}{{\sin x}}.

A.  
D=R\{π2+kπ,k∈Z}.{\rm{D}} = R\backslash \left\{ {\dfrac{\pi }{2} + k\pi ,k \in Z} \right\}.
B.  
D=R{\rm{D}} = R
C.  
D=R\{0}.{\rm{D}} = R\backslash \left\{ 0 \right\}.
D.  
D=R\{kπ,k∈Z}.{\rm{D}} = R\backslash \left\{ {k\pi ,k \in Z} \right\}.
Câu 12: 1 điểm

Trong mặt phẳng với hệ tọa độ Oxy, cho hình vuông ABCD. Gọi M(1;3) là trung điểm của cạnh BC, N(−32;12)N\left( { - \dfrac{3}{2};\dfrac{1}{2}} \right) là điểm trên cạnh AC sao cho AN=14ACAN = \dfrac{1}{4}AC . Xác định tọa độ điểm D, biết D nằm trên đường thẳng x−y−3=0x - y - 3 = 0

A.  
(1;2).
B.  
(1;-2).
C.  
(-2;1).
D.  
(2;1).
Câu 13: 1 điểm

Cho hình chóp S.ABCDS.ABCD có đáy ABCDABCD là hình vuông, SA⊥(ABCD).SA \bot \left( {ABCD} \right). Khẳng định nào dưới đây sai?

A.  
SD⊥ACSD \bot AC
B.  
BC⊥SBBC \bot SB
C.  
CD⊥SDCD \bot SD
D.  
SA⊥BDSA \bot BD
Câu 14: 1 điểm

Cho hàm số y=f(x)y = f(x) , biết rằng hàm số y=f′(x−2)+2y = f'(x - 2) + 2 có đồ thị như hình vẽ bên. Hỏi hàm số y=f(x)y = f(x) nghịch biến trên khoảng nào trong các khoảng dưới đây?

A.  
(−∞;2).( - \infty ;2).
B.  
(−1;1).( - 1;1).
C.  
(2;+∞).(2; + \infty ).
D.  
(32;52).\left( {\dfrac{3}{2};\dfrac{5}{2}} \right).
Câu 15: 1 điểm

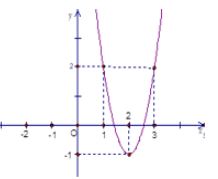
Đồ thị hình bên là của hàm số nào?

A.  
y=−x4+2x2+2y = - {x^4} + 2{x^2} + 2 .
B.  
y=x4−2x2+2y = {x^4} - 2{x^2} + 2 .
C.  
y=x4−4x2+2y = {x^4} - 4{x^2} + 2 .
D.  
y=x4−2x2+3y = {x^4} - 2{x^2} + 3 .
Câu 16: 1 điểm

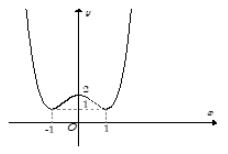
Cho hàm số y=2x+1x+1y = \dfrac{{2x + 1}}{{x + 1}} , chọn mệnh đề đúng ?

A.  
Hàm số nghịch biến trên các khoảng (−∞;−1)\left( { - \infty ; - 1} \right) và (−1;+∞)\left( { - 1; + \infty } \right) .
B.  
Hàm số đồng biến trên R\{−1}R\backslash \left\{ { - 1} \right\} .
C.  
Hàm số nghịch biến trên R\{−1}R\backslash \left\{ { - 1} \right\} .
D.  
Hàm số đồng biến trên các khoảng (−∞;−1)\left( { - \infty ; - 1} \right) và (−1;+∞)\left( { - 1; + \infty } \right) .
Câu 17: 1 điểm

Gọi giá trị lớn nhất và nhỏ nhất của hàm số y=x4+2x2−1y = {x^4} + 2{x^2} - 1 trên đoạn [−1;2]\left[ { - 1;2} \right] lần lượt là MM và mm . Khi đó, giá trị của M.mM.m là:

A.  
−46 - 46
B.  
−23 - 23
C.  
−2 - 2
D.  
4646
Câu 18: 1 điểm

Cho hàm số f(x)f\left( x \right) xác định trên R\{0}R\backslash {\rm{\{ 0\} }} , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:

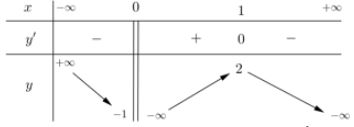
Hàm số đã cho có bao nhiêu điểm cực trị ?

A.  
3
B.  
1
C.  
2
D.  
0
Câu 19: 1 điểm

Cho hình chóp S.ABCDS.ABCD có đáy ABCDABCD là hình vuông, SASA vuông góc với đáy, mặt bên (SCD)\left( {SCD} \right) hợp với đáy một góc bằng 60∘60^\circ , MM là trung điểm của BCBC . Biết thể tích khối chóp S.ABCDS.ABCD bằng a333\dfrac{{{a^3}\sqrt 3 }}{3} . Khoảng cách từ MM đến mặt phẳng (SCD)\left( {SCD} \right) bằng:

A.  
a36\dfrac{{a\sqrt 3 }}{6} .
B.  
a3a\sqrt 3 .
C.  
a34\dfrac{{a\sqrt 3 }}{4} .
D.  
a32\dfrac{{a\sqrt 3 }}{2} .
Câu 20: 1 điểm

Tính lim⁡x→−∞(4x2+8x+1+2x)\mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {4{x^2} + 8x + 1} + 2x} \right) bằng

A.  
00
B.  
+∞ + \infty
C.  
−2 - 2
D.  
−∞ - \infty
Câu 21: 1 điểm

Cho hình chóp S.ABCDS.ABCD có đáy ABCDABCD là hình vuông cạnh aa , tâm OO . Cạnh bên SA=2aSA = 2a và vuông góc với mặt đáy (ABCD)\left( {ABCD} \right) . Gọi HH và KK lần lượt là trung điểm của cạnh BCBC và CDCD . Tính khoảng cách giữa hai đường thẳng HKHK và SDSD .

A.  
a3.\dfrac{a}{3}.
B.  
2a3.\dfrac{{2a}}{3}.
C.  
a32\dfrac{{a\sqrt 3 }}{2} .
D.  
a2.\dfrac{a}{2}.
Câu 22: 1 điểm

Cho hàm số y=2x+1x−1y = \dfrac{{2x + 1}}{{x - 1}} xác định trên R\{1} . Đạo hàm của hàm số là:

A.  
y′=−3(x−1)2y' = - \dfrac{3}{{{{(x - 1)}^2}}}
B.  
y′=1(x−1)2y' = \dfrac{1}{{{{(x - 1)}^2}}}
C.  
y′=3(x−1)2y' = \dfrac{3}{{{{(x - 1)}^2}}}
D.  
y′=2y' = 2
Câu 23: 1 điểm

Thể tích khối lập phương có cạnh bằng 2cm bằng:

A.  
6cm36c{m^3} .
B.  
8cm8cm
C.  
6cm26c{m^2}
D.  
8cm38c{m^3}
Câu 24: 1 điểm

Cho dãy số ( un{u_n} ) xác định bởi u1=1{u_1} = 1 ; un+1=32(un−n+4n2+3n+2){u_{n + 1}} = \dfrac{3}{2}\left( {{u_n} - \dfrac{{n + 4}}{{{n^2} + 3n + 2}}} \right) . Tìm u50{u_{50}} ?

A.  
-312540600.
B.  
-212540500.
C.  
-312540500.
D.  
-212540600.
Câu 25: 1 điểm

Cho phương trình sin⁡2x−sin⁡x−2mcos⁡x+m=0,\sin 2x - \sin x - 2m\cos x + m = 0,mm là tham số. Số các giá trị nguyên của mm để phương trình đã cho có đúng hai nghiệm phân biệt trên [7π4;  3π]\left[ {\dfrac{{7\pi }}{4};\,\,3\pi } \right] là:

A.  
3
B.  
2
C.  
0
D.  
1
Câu 26: 1 điểm

Cho hàm số y=f(x)y = f(x) . Hàm số y=f′(x)y = f'(x) có đồ thị như hình vẽ dưới đây.

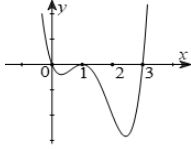
Có bao nhiêu giá tri nguyên của mm để hàm số y=f(x2+m)y = f({x^2} + m) có 33 điểm cực trị.

A.  
3
B.  
4
C.  
2
D.  
1
Câu 27: 1 điểm

Tiếp tuyến của đồ thị hàm số y = 4x − 1 y\, = \,\dfrac{4}{{x\, - \,1}}\, tại điểm có hoành độ x0 = - 1 có phương trình là:

A.  
y = x + 2
B.  
y = x -1
C.  
y = - x + 2
D.  
y = - x – 3.
Câu 28: 1 điểm

Cho hàm số y=f(x)y = f(x) có đồ thị như hình vẽ dưới đây. Hàm số y=f(x)y = f(x) có bao nhiêu điểm cực tiểu?

A.  
1
B.  
0
C.  
3
D.  
2
Câu 29: 1 điểm

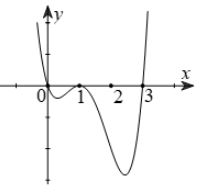
Cho hàm số y=f(x)y = f\left( x \right) có đạo hàm f′(x)f'(x) trên R. Đồ thị hình bên là của hàm số y=f′(x)y = f'(x) . Hỏi hàm số y=f(x)y = f\left( x \right) đồng biến trên khoảng nào trong các khoảng dưới đây?

A.  
(1;2)\left( {1;2} \right) .
B.  
(0;1)\left( {0;1} \right) .
C.  
(−∞;2).\left( { - \infty ;2} \right).
D.  
(2;+∞)\left( {2; + \infty } \right) .
Câu 30: 1 điểm

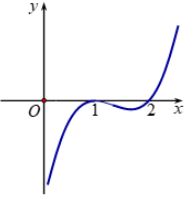
Mệnh đề nào sau đây sai?

A.  
Ba điểm A, B, CA,\,B,\,C bất kì thì AC  →=AB  →+BC  →\overrightarrow {AC\,\,} = \overrightarrow {AB\,\,} + \overrightarrow {BC\,\,} .
B.  
II là trung điểm ABAB thì MI  →=MA  →+MB  →\overrightarrow {MI\,\,} = \overrightarrow {MA\,\,} + \overrightarrow {MB\,\,} với mọi điểm MM .
C.  
ABCDABCD là hình bình hành thì AC  →=AB  →+AD  →\overrightarrow {AC\,\,} = \overrightarrow {AB\,\,} + \overrightarrow {AD\,\,} .
D.  
GG là trọng tâm ΔABC\Delta ABC thì GA  →+GB  →+GC  →=0  →\overrightarrow {GA\,\,} + \overrightarrow {GB\,\,} + \overrightarrow {GC\,\,} = \overrightarrow {0\,\,} .
Câu 31: 1 điểm

Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số f(x)=2cos⁡3x−cos⁡2xf\left( x \right) = 2{\cos ^3}x - \cos 2x trên tập hợp D=[−π3;π3]D = \left[ { - \dfrac{\pi }{3};\dfrac{\pi }{3}} \right]

A.  
max⁡x∈Df(x)=1,  min⁡x∈Df(x)=1927\mathop {\max }\limits_{x \in D} f\left( x \right) = 1,\,\,\mathop {\min }\limits_{x \in D} f\left( x \right) = \dfrac{{19}}{{27}} .
B.  
max⁡x∈Df(x)=34,  min⁡x∈Df(x)=−3\mathop {\max }\limits_{x \in D} f\left( x \right) = \dfrac{3}{4},\,\,\mathop {\min }\limits_{x \in D} f\left( x \right) = - 3 .
C.  
max⁡x∈Df(x)=34,  min⁡x∈Df(x)=1927\mathop {\max }\limits_{x \in D} f\left( x \right) = \dfrac{3}{4},\,\,\mathop {\min }\limits_{x \in D} f\left( x \right) = \dfrac{{19}}{{27}} .
D.  
max⁡x∈Df(x)=1,  min⁡x∈Df(x)=−3\mathop {\max }\limits_{x \in D} f\left( x \right) = 1,\,\,\mathop {\min }\limits_{x \in D} f\left( x \right) = - 3 .
Câu 32: 1 điểm

Giá trị nhỏ nhất của hàm số y=2x+11−xy = \dfrac{{2x + 1}}{{1 - x}} trên đoạn [ 2 ; 3 ] bằng:

A.  
1
B.  
-2
C.  
0
D.  
-5
Câu 33: 1 điểm

Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh A có thể tích V. Tính V.

A.  
V=2a318V = \dfrac{{\sqrt 2 {a^3}}}{{18}}
B.  
V=112a3216V = \dfrac{{11\sqrt 2 {a^3}}}{{216}}
C.  
V=132a3216V = \dfrac{{13\sqrt 2 {a^3}}}{{216}}
D.  
V=72a3216V = \dfrac{{7\sqrt 2 {a^3}}}{{216}}
Câu 34: 1 điểm

Cho hàm số y=f(x)y = f(x) có đạo hàm liên tục trên R,\mathbb{R}, hàm số y=f′(x−2)y = f'(x - 2) có đồ thị như hình bên. Số điểm cực trị của hàm số y=f(x)y = f(x) là

A.  
3
B.  
2
C.  
0
D.  
1
Câu 35: 1 điểm

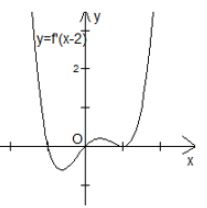
Trong mặt phẳng Oxy ,cho A(3;-10), B(-5;4). Tọa độ của vectơ AB→\overrightarrow {AB} là :

A.  
AB→=(−8;14)\overrightarrow {AB} = \left( { - 8;14} \right)
B.  
AB→=(8;14)\overrightarrow {AB} = \left( {8;14} \right)
C.  
AB→=(7;−4)\overrightarrow {AB} = \left( {7; - 4} \right)
D.  
AB→=(7;4)\overrightarrow {AB} = \left( {7;4} \right)
Câu 36: 1 điểm

Tìm số tự nhiên nn thỏa mãn Cn01.2+Cn12.3+Cn23.4+...+Cnn(n+1)(n+2)=22018−n−3(n+1)(n+2)\dfrac{{C_n^0}}{{1.2}} + \dfrac{{C_n^1}}{{2.3}} + \dfrac{{C_n^2}}{{3.4}} + ... + \dfrac{{C_n^n}}{{\left( {n + 1} \right)\left( {n + 2} \right)}} = \dfrac{{{2^{2018}} - n - 3}}{{\left( {n + 1} \right)\left( {n + 2} \right)}} .

A.  
n=2017n = 2017 .
B.  
n=2019n = 2019 .
C.  
n=2018n = 2018 .
D.  
n=2016n = 2016 .
Câu 37: 1 điểm

Đồ thị sau đây là của hàm số y=x4−3x2−3y = {x^4} - 3{x^2} - 3 . Với giá trị nào của m thì phương trình x4−3x2+m=0{x^4} - 3{x^2} + m = 0 có ba nghiệm phân biệt ?

A.  
m = -3
B.  
m = - 4
C.  
m = 0
D.  
m = 4
Câu 38: 1 điểm

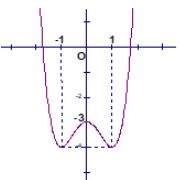
Cho hàm số y=2mx+1x−m y = \dfrac{{2mx + 1}}{{x - m}}\, với tham số me0m e 0 . Giao điểm hai đường tiệm cận của đồ thị hàm số thuộc đường thẳng có phương trình nào dưới đây ?

A.  
2x+y=0.2x + y = 0.
B.  
y=2x.y = 2x.
C.  
x−2y=0.x - 2y = 0.
D.  
x+2y=0.x + 2y = 0.
Câu 39: 1 điểm

Cho hình chóp tam giác đều S.ABC có cạnh AB bằng a. Các cạnh bên SA, SB, SC tạo với đáy một góc 60o. Gọi D là giao điểm của SA với mặt phẳng qua BC và vuông góc với SA. Tính theo a thể tích khối chóp S.DBC

A.  
5a396\dfrac{{5{a^3}}}{{96}}
B.  
5a3296\dfrac{{5{a^3}\sqrt 2 }}{{96}}
C.  
5a3396\dfrac{{5{a^3}\sqrt 3 }}{{96}}
D.  
5a3596\dfrac{{5{a^3}\sqrt 5 }}{{96}}
Câu 40: 1 điểm

Tính số chỉnh hợp chập 55 của 88 phần tử.

A.  
67206720
B.  
5656
C.  
4032040320
D.  
336336
Câu 41: 1 điểm

Đồ thị của hàm số y=x3−3x2−9x+1y = {x^3} - 3{x^2} - 9x + 1 có hai điểm cực trị A và B. Điểm nào dưới đây thuộc đường thẳng AB?

A.  
P(1;0)P(1;0)
B.  
M(0;−1)M(0; - 1)
C.  
N(1;−10)N(1; - 10)
D.  
Q(−1;10)Q( - 1;10)
Câu 42: 1 điểm

Cho dãy số (un)\left( {{u_n}} \right) với un=3(−1)nn.{u_n} = 3{\left( { - 1} \right)^n}n. Khẳng định nào sau đây sai?

A.  
u2=−6{u_2} = - 6
B.  
u1=−3{u_1} = - 3
C.  
u4=12{u_4} = 12
D.  
u3=−9{u_3} = - 9
Câu 43: 1 điểm

Đường thẳng nào dưới đây là đường tiệm cận ngang của đồ thị hàm số y=3−2xx−1y = \dfrac{{3 - 2x}}{{x - 1}} ?

A.  
y=3y = 3 .
B.  
x=−2x = - 2 .
C.  
x=1x = 1 .
D.  
y=−2y = - 2 .
Câu 44: 1 điểm

Tính thể tích VV của khối lăng trụ tam giác đều có tất cả các cạnh bằng aa .

A.  
V=a332V = \dfrac{{{a^3}\sqrt 3 }}{2} .
B.  
V=a333V = \dfrac{{{a^3}\sqrt 3 }}{3} .
C.  
V=a334V = \dfrac{{{a^3}\sqrt 3 }}{4} .
D.  
V=a33V = \dfrac{{{a^3}}}{3} .
Câu 45: 1 điểm

Nghiệm của phương trình 3sin⁡2x+cos⁡2x−2=0\sqrt 3 \sin 2x + \cos 2x - 2 = 0 là:

A.  
x=π3+k2πx = \dfrac{\pi }{3} + k2\pi
B.  
x=π6+k2πx = \dfrac{\pi }{6} + k2\pi
C.  
x=π3+kπx = \dfrac{\pi }{3} + k\pi
D.  
x=π6+kπx = \dfrac{\pi }{6} + k\pi
Câu 46: 1 điểm

Cho khối chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D; AB = AD = 2a;CD = a . Góc giữa hai mặt phẳng (SBC) và (ABCD) bằng 600 . Gọi I là trung điểm của AD. Biết 2 mặt phẳng (SBI) và (SCI) cùng vuông góc với mặt phẳng (ABCD). Tính thể tích khối chóp S.ABCD.

A.  
VS.ABCD=6a33{V_{S.ABCD}} = 6{a^3}\sqrt 3
B.  
VS.ABCD=6a3155{V_{S.ABCD}} = \dfrac{{6{a^3}\sqrt {15} }}{5}
C.  
VS.ABCD=3a3155{V_{S.ABCD}} = \dfrac{{3{a^3}\sqrt {15} }}{5}
D.  
VS.ABCD=6a3{V_{S.ABCD}} = 6{a^3}
Câu 47: 1 điểm

Cho hình chữ nhật MNPQ.MNPQ. Phép tịnh tiến theo véc tơ MN→\overrightarrow {MN} biến điểm QQ thành điểm nào?

A.  
Điểm N.N.
B.  
Điểm M.M.
C.  
Điểm P.P.
D.  
Điểm Q.Q.
Câu 48: 1 điểm

Trong mặt phẳng với hệ tọa độ OxyOxy cho các điểm A(1; 2), B(3; −1), C(0; 1)A\left( {1;\,2} \right),\,B\left( {3;\, - 1} \right),\,C\left( {0;\,1} \right) . Tọa độ của véctơ u →=2AB→+BC→\overrightarrow {u\,} = 2\overrightarrow {AB} + \overrightarrow {BC} là:

A.  
u →(2; 2)\overrightarrow {u\,} \left( {2;\,2} \right) .
B.  
u →(1; −4)\overrightarrow {u\,} \left( {1;\, - 4} \right) .
C.  
u →(−4; 1)\overrightarrow {u\,} \left( { - 4;\,1} \right) .
D.  
u →(−1; 4)\overrightarrow {u\,} \left( { - 1;\,4} \right) .
Câu 49: 1 điểm

Cho phương trình: 2x3+x2−2x+m−2x2+x+x3−3x+m=0{2^{{x^3} + {x^2} - 2x + m}} - {2^{{x^2} + x}} + {x^3} - 3x + m = 0 . Tập các giá trị mm để phương trình có 3 nghiệm phân biệt có dạng (a;b)\left( {a;b} \right) . Tổng (a+2b)\left( {a + 2b} \right) bằng:

A.  
1
B.  
0
C.  
-2
D.  
2
Câu 50: 1 điểm

Hệ số của số hạng chứa x7{x^7} trong khai triển nhị thức (x−2xx)12{\left( {x - \dfrac{2}{{x\sqrt x }}} \right)^{12}} (với x>0x > 0 ) là:

A.  
376.
B.  
−264 - 264 .
C.  
264.
D.  
260.

Xem thêm đề thi tương tự

thumbnail
[2022] Trường THPT Nghi Xuân - Đề thi thử THPT QG năm 2022 môn Toán
Chưa có mô tả

50 câu hỏi 1 mã đề 1 giờ

217,066 lượt xem 116,879 lượt làm bài

Bạn chưa chinh phục đề thi này!!!
thumbnail
[2022] Trường THPT Nghi Xuân - Đề thi thử THPT QG năm 2022 môn Vật Lý
Chưa có mô tả

40 câu hỏi 1 mã đề 1 giờ

192,612 lượt xem 103,712 lượt làm bài

Bạn chưa chinh phục đề thi này!!!
thumbnail
[2022] Trường THPT Long Trường - Đề thi thử THPT QG năm 2022 môn Toán
Chưa có mô tả

50 câu hỏi 1 mã đề 1 giờ

193,597 lượt xem 104,237 lượt làm bài

Bạn chưa chinh phục đề thi này!!!
thumbnail
[2022] Trường THPT Thanh Xuân - Đề thi thử THPT QG năm 2022 môn Toán
Chưa có mô tả

50 câu hỏi 1 mã đề 1 giờ

221,452 lượt xem 119,238 lượt làm bài

Bạn chưa chinh phục đề thi này!!!
thumbnail
[2022] Trường THPT Phú Xuân - Đề thi thử THPT QG năm 2022 môn Vật Lý
Chưa có mô tả

40 câu hỏi 1 mã đề 1 giờ

209,779 lượt xem 112,952 lượt làm bài

Bạn chưa chinh phục đề thi này!!!
thumbnail
[2022] Trường THPT Phú Xuân - Đề thi thử THPT QG năm 2022 môn Sinh Học
Chưa có mô tả

40 câu hỏi 1 mã đề 1 giờ

209,631 lượt xem 112,875 lượt làm bài

Bạn chưa chinh phục đề thi này!!!
thumbnail
[2022] Trường THPT Lê Minh Xuân - Đề thi thử THPT QG năm 2022 môn Toán
Chưa có mô tả

50 câu hỏi 1 mã đề 1 giờ

201,282 lượt xem 108,381 lượt làm bài

Bạn chưa chinh phục đề thi này!!!
thumbnail
[2022] Trường THPT Thanh Xuân - Đề thi thử THPT QG năm 2022 môn Toán
Chưa có mô tả

50 câu hỏi 1 mã đề 1 giờ

199,598 lượt xem 107,471 lượt làm bài

Bạn chưa chinh phục đề thi này!!!
thumbnail
[2022] Trường THPT Xuân Giang - Đề thi thử THPT QG năm 2022 môn Sinh
Chưa có mô tả

40 câu hỏi 1 mã đề 1 giờ

217,013 lượt xem 116,851 lượt làm bài

Bạn chưa chinh phục đề thi này!!!