Bài toán về điểm biểu diễn số phức trong mặt

Tìm điểm M biểu diễn số phức \[z = i - 2\]

Cho số phức z thỏa mãn \[(1 + i)z = 3 - i\]. Hỏi điểm biểu diễn của z là điểm nào trong các điểm M,N,P,Q ở hình bên ?

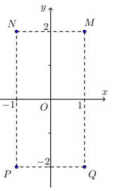
Cho số phức \[z = 2 + 5i\]. Tìm số phức \[w = iz + \overline z \]

Hỏi có bao nhiêu số phức thỏa mãn đồng thời các điều kiện \[\left| {z - i} \right| = 5\] và \[{z^2}\] là số thuần ảo?

Cho số phức z thỏa mãn (2−i)z=7−i . Hỏi điểm biểu diễn của z là điểm nào trong các điểm M,N,P,Q ở hình dưới.

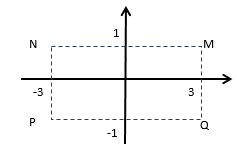
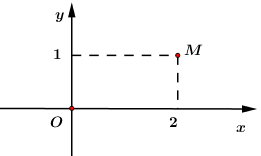
Trên mặt phẳng tọa độ, điểm M là điểm biểu diển của số phức z (như hình vẽ bên). Điểm nào trong hình vẽ là điểm biểu diển của số phức 2z?

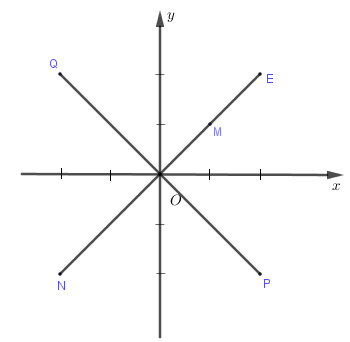
Số phức z thỏa mãn \[\left| z \right| + z = 0\]. Khi đó:

Cho ba điểm A,B,C lần lượt biểu diễn các số phức sau \[{z_1} = 1 + i;{z_2} = z_1^2;{z_3} = m - i\]. Tìm các giá trị thực của m sao cho tam giác ABC vuông tại B.

Cho số phức z thỏa mãn $\left| z \right| = \frac{{\sqrt 2 }}{2}$ và điểm A trong hình vẽ bên là điểm biểu diễn của z. Biết rằng trong hình vẽ bên, điểm biểu diễn của số phức \[{\rm{w}} = \frac{1}{{iz}}\] là một trong bốn điểm M,N,P,Q. Khi đó điểm biểu diễn của số phức w là

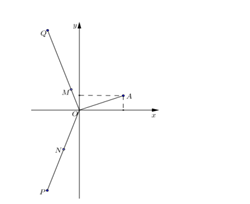
Gọi M và N lần lượt là điểm biểu diễn của các số phức \[{z_1};{z_2}\;\] khác 0. Khi đó khẳng định nào sau đây sai ?

Số phức z được biểu diễn trên trên mặt phẳng như hình vẽ.

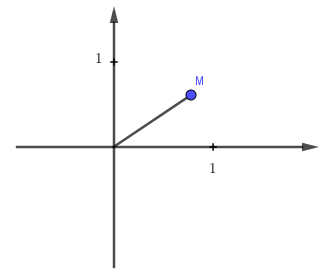
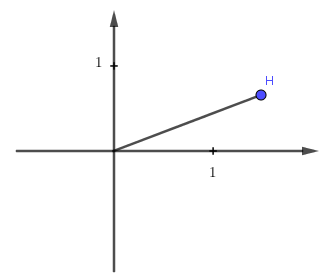
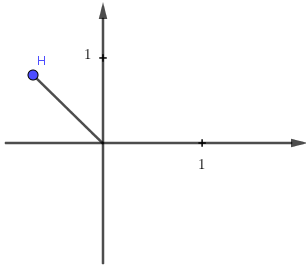
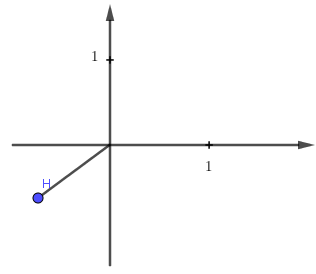
Hỏi hình nào biểu diễn cho số phức \[w = \frac{i}{{\overline z }}\]

Trong mặt phẳng phức gọi A,B,C lần lượt là các điểm biểu diễn của các số phức \[{z_1} = 3 + 2i;{z_2} = 3 - 2i;{z_3} = - 3 - 2i\]. Khẳng định nào sau đây là sai?

Tập điểm biểu diễn số phức z thỏa mãn \[{\left| z \right|^2} = {z^2}\] là:

Cho các số phức z thỏa mãn \[\left| {z + 1 - i} \right| = \left| {z - 1 + 2i} \right|.\]Tập hợp các điểm biểu diễn các số phức z trên mặt phẳng tọa độ là một đường thẳng. Viết phương trình đường thẳng đó

Giả sử\[z = a + bi\left( {a,b \in R} \right)\]Ta có

\[\begin{array}{*{20}{l}}{\left| {z + 1 - i} \right| = \left| {z - 1 + 2i} \right| \Leftrightarrow \left| {\left( {a + 1} \right) + \left( {b - 1} \right)i} \right| = \left| {\left( {a - 1} \right) + \left( {b + 2} \right)i} \right|}\\{ \Leftrightarrow {{\left( {a + 1} \right)}^2} + {{\left( {b - 1} \right)}^2} = {{\left( {a - 1} \right)}^2} + {{\left( {b + 2} \right)}^2}}\\{ \Leftrightarrow 4a - 6b - 3 = 0}\end{array}\]

Vậy phương trình đường thẳng cần tìm là \[4x - 6y - 3 = 0\]

Cho số phức z thỏa mãn \[{\left( {1 + z} \right)^2}\] là số thực. Tập hợp điểm MM biểu diễn số phức z là:

Cho số phức z thay đổi, luôn có \[\left| z \right| = 2\;\]. Khi đó tập hợp điểm biểu diễn số phức \[w = \left( {1 - 2i} \right)\overline z + 3i\;\] là

Cho các số phức z thỏa mãn \[\left| z \right| = 4\;\]. Biết rằng tập hợp các điểm biểu diễn số phức\[w = \left( {3 + 4i} \right)z + i\;\]là một đường tròn. Tính bán kính r của đường tròn đó.

Tập hợp các điểm trong mặt phẳng tọa độ biểu diễn số phức z thoả mãn điều kiện \[2\left| {z - i} \right| = \left| {z - \overline z + 2i} \right|\] là hình gì?

Trên mặt phẳng tọa độ Oxy, tìm tập hợp các điểm biểu diễn các số phức zz thỏa mãn điều kiện \[\left| {z - 2} \right| + \left| {z + 2} \right| = 10.\]

Cho số phức \[z = \left( {m + 3} \right) + \left( {{m^2} - m - 6} \right)i\] với \[m \in \mathbb{R}\] Gọi (P) là tập hợp điểm biểu diễn số phức z trong mặt phẳng tọa độ. Diện tích hình phẳng giới hạn bởi (P) và trục hoành bằng

Cho hai số phức \[{z_1},{z_2}\;\] thỏa mãn \[\left| {{z_1}} \right| = 6,\left| {{z_2}} \right| = 2\]. Gọi M,N lần lượt là các điểm biểu diễn của số phức \[{z_1}\] và số phức \[i{z_2}_{}\]. Biết $\widehat {MON} = {60^ \circ }$ . Tính \[T = \left| {z_1^2 + 9z_2^2} \right|\]

Trên mặt phẳng tọa độ Oxy, gọi M là điểm biểu diễn hình học của số phức \[z = - 1 + 2i\;\] và \[\alpha \] là góc lượng giác có tia đầu Ox, tia cuối OM. Tính \[tan2\alpha .\]

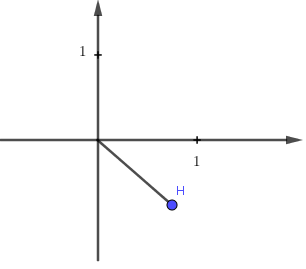
Biết rằng điểm biểu diễn số phức z là điểm M ở hình bên dưới. Modun của z bằng:

Gọi A và B lần lượt là điểm biểu diễn của số phức \[{z_1} = 3 - 2i\;\] và \[{z_2} = 1 + 4i.\] Trung điểm của đoạn thẳng AB có tọa độ là:

Cho các số phức \[{z_1} = 3 - 2i,{z_2} = 1 + 4i\] và \[{z_3} = - 1 + i\;\] có biểu diễn hình học trong mặt phẳng tọa độ Oxy lần lượt là các điểm A,B,C. Diện tích tam giác ABC bằng:

Cho hai số phức \[{z_1} = 3 + i,{z_2} = - 1 + 2i\]. Trong mặt phẳng tọa độ, điểm biểu diễn cho số phức \[w = 2{z_1} - {z_2}\;\] là:

Trong mặt phẳng phức, tập hợp các điểm biểu diễn các số phức z thỏa mãn \[z.\overline z = 1\;\] là:

Trong mặt phẳng phức, gọi A, B, C, D lần lượt là các điểm biểu diễn các số phức \[{z_1} = - 1 + i,\;{z_2} = 1 + 2i,{z_3} = 2 - i,{z_4} = - 3i\]. Gọi S diện tích tứ giác ABCD. Tính S.

Cho các số phức \[{z_1} = 2,{z_2} = - 4i,{z_3} = 2 - 4i\] có điểm biểu diễn tương ứng trên mặt phẳng tọa độ Oxy là A, B, C. Diện tích tam giác ABC bằng

Cho các số phức z thỏa mãn \[\left| z \right| = {\rm{ }}2\]và điểm A trong hình vẽ là điểm biểu diễn của z. Biết rằng trong hình vẽ, điểm biểu diễn số phức \[w = \frac{{ - 4}}{z}\] là một trong bốn điểm M, N, P, Q

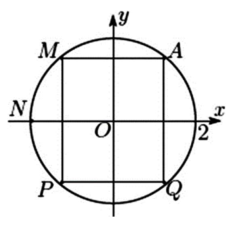
Khi đó điểm biểu diễn của số phức w là