
Bộ đề kiểm tra Học kỳ 2 Toán 12 online có đáp án mới nhất
Từ khoá: đề thi Toán 12 kiểm tra học kỳ 2 đề thi online Toán 12 đề thi mới nhất đáp án chi tiết luyện thi học kỳ toán lớp 12 số phức tích phân xác suất hình học không gian
Đề thi nằm trong bộ sưu tập: TOÁN 12
Số câu hỏi: 713 câuSố mã đề: 15 đềThời gian: 45 phút
174,615 lượt xem 13,425 lượt làm bài
Xem trước nội dung:
Số phức liên hợp của z thỏa mãn 3z = 3 + 6i là:
Cho hàm số y = f (x) liên tục trên đoạn [a; b]. Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y = f (x), trục hoành và hai đường thẳng x = a, x = b (a < b). Thể tích của khối tròn xoay tạo thành khi quay D quanh trục hoành được tính theo công thức:
Cho hàm số f (x) liên tục trên [a; b] và F (x) là một nguyên hàm của f (x). Tìm khẳng định sai.
Phương trình nào sau đây là phương trình bậc hai với hệ số thực?
bằng
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1; 0; 2) và B(4; 1; 1) Vectơ có tọa độ là:
Cho hai số phức z1 = 3 + i và z2 = 3 - i. Tính tích z1z2
Trong không gian Oxyz, cho mặt phẳng (P) có phương trình 3x + 2y + z + 1 = 0. Tìm một vectơ pháp tuyến của (P).
Trong không gian với hệ tọa độ Oxyz, cho . Tọa độ của là
Số phức 6 + 5i có phần thực bằng:
Trong không gian Oxyz, cho đường thẳng ∆ có phương trình chính tắc . Một véc tơ chỉ phương của đường thẳng ∆ là
Số phức có tổng phần thực và phần ảo bằng:
Trong không gian Oxyz. Điểm nào sau đây thuộc mặt phẳng (P): -2x + y - 5 = 0?
Biết tích phân và . Khi đó bằng
Trong không gian Oxyz, phương trình nào sau đây là phương trình tham số của đường thẳng d qua điểm M (2; 3; 1) và có vectơ chỉ phương ?
Số phức liên hợp của số phức 1 - 2i là:
Hàm số F (x) là một nguyên hàm của hàm số f (x) trên khoảng K nếu
Họ nguyên hàm của hàm số f (x) = 2sin x là
Trong không gian Oxyz, cho ba điểm M(1; 3; 2), N(-1; 2; 1), P(1; 2; -1). Lập phương trình tham số của đường thẳng đi qua điểm M và song song với NP.
Diện tích hình phẳng giới hạn bởi hai đường y = x2 + 1 và y = 2x + 1 bằng
Tính tích phân bằng cách đặt , mệnh đề nào dưới đây đúng?
Trong không gian Oxyz, cho hai điểm A(1; 0; -1), B(2; 1; -1). Lập phương trình mặt phẳng trung trực của đoạn AB.
Tìm nguyên hàm của hàm số .
Cho hình phẳng D giới hạn bởi đường cong , trục hoành và các đường thẳng . Khối tròn xoay tạo thành khi quay D quay quanh trục hoành có thể tích V bằng bao nhiêu?
Trong hình vẽ bên, điểm M biểu diễn số phức .
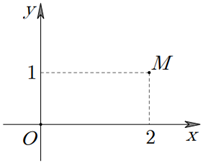
Số phức z là:
Gọi z1 và z2 là hai nghiệm phức của phương trình 3z2 - z + 1 = 0. Tính P = |z1| + |z2|.
Tìm môđun của số phức z, biết
Cho số phức z = 2 - 5i. Tìm số phức .
Trong không gian Oxyz, cho điểm M(3; 1; -2) và mặt phẳng (a): 3x - y + 2z + 4 = 0. Mặt phẳng (P) đi qua M và song song với (a) có phương trình là
Trong mặt phẳng phức Oxy, gọi M là điểm biểu diễn số phức z = 4 - 3i. Tính độ dài đoạn thẳng OM.
Cho tích phân , với a; b Î ℤ. Tính a - b.
Trên khoảng thì bằng
Cho . Giá trị của bằng
Trong không gian Oxyz, (a) là mặt phẳng đi qua điểm A(2; -1; 5) và vuông góc với hai mặt phẳng (P): 3x - 2y + z = 0 và (Q): 5x - 4y + 3z + 1 = 0. Lập phương trình của mặt phẳng (a).
Cho hàm số f (x) liên tục trên ℝ và f (3) = 12, . Tính .
A.
B.
Có bao nhiêu số phức z thỏa mãn là số thuần ảo và |z - 2i| = 1?
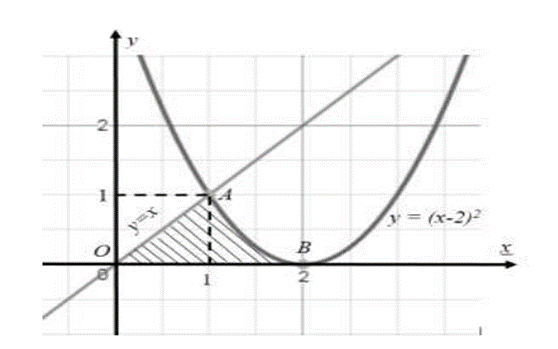
Tính diện tích phần hình phẳng gạch chéo (tam giác cong OAB) trong hình vẽ bên.
Trong không gian Oxyz, cho hai điểm A (1; -1; 2), B(1; 3; 4). Tìm tọa độ điểm M trên trục hoành Ox sao cho biểu thức P = MA2 + MB2 đạt giá trị nhỏ nhất.
Biết F (x) là một nguyên hàm của hàm số f (x) = e3x và F (0) = 0. Giá trị của F (ln3) bằng
Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số y = 2(x - 1)ex, trục tung và trục hoành. Tính thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox
Trong không gian Oxyz, cho hai mặt phẳng: (P): 5x - 3y + 2z - 19 = 0, (Q): x - y + z - 3 = 0. Tìm phương trình đường thẳng ∆ là giao tuyến của hai mặt phẳng (P), (Q).
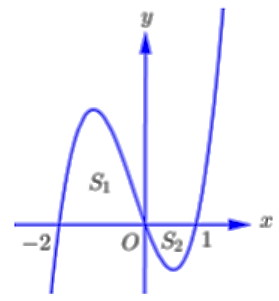
Cho hình phẳng giới hạn bởi đồ thị hàm số y = f (x) và trục hoành gồm 2 phần, phần nằm phía trên trục hoành có diện tích và phần nằm phía dưới trục hoành có diện tích . Tính
Trong không gian Oxyz, cho mặt phẳng (P) : x - 2y + 2z - 5 = 0 và hai điểm A(-3; 0; 1), B(1; -1; 3). Tìm phương trình của đường thẳng ∆ đi qua A và song song với (P) sao cho khoảng cách từ B đến đường thẳng ∆ là nhỏ nhất.
Cho hai số phức z1, z2, thỏa mãn |z1 + 6| = 5, |z2 + 2 - 3i| = |z2 - 2 - 6i|. Giá trị nhỏ nhất của |z1 - z2| bằng
Trong không gian Oxyz, cho mặt cầu (S) có tâm thuộc mặt phẳng (P): x + 2y + z - 7 = 0 và đi qua hai điểm A(1; 2; 1), B(2; 5; 3). Bán kính nhỏ nhất của mặt cầu (S) bằng
Đề thi tương tự
14 mã đề 200 câu hỏi 1 giờ
177,314 xem13,625 thi
19 mã đề 282 câu hỏi 1 giờ
185,362 xem14,241 thi
15 mã đề 169 câu hỏi 1 giờ
151,910 xem11,678 thi
15 mã đề 180 câu hỏi 1 giờ
162,081 xem12,462 thi
5 mã đề 71 câu hỏi 1 giờ
188,969 xem14,528 thi
10 mã đề 144 câu hỏi 1 giờ
186,103 xem14,306 thi
