Trắc nghiệm Hai đường thẳng chéo nhau và hai đường thẳng song song có đáp án

Trong các phát biểu sau, phát biểu nào đúng?

Trong không gian cho ba đường thẳng a, b và c. Trong các phát biểu sau, phát biểu nào là đúng?

Cho hai đường thẳng a và b chéo nhau. Một đường thẳng c song song với a. khẳng định nào sau đây là đúng?

Cho hình chóp S.ABCD có đáy là hình bình hành. M là trung điểm của SC. Tìm giao tuyến của (MAB) với (SCD).

Cho hình chóp S. ABCD có đáy là hình thang với các cạnh đáy là AB, CD. Gọi I, J lần lượt là trung điểm của AD, BC và G là trọng tâm tam giác SAB. Tìm thiết diện của hình chóp S.ABCD cắt bởi (IJG)

Hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Trên cạnh AC lấy điểm M và trên cạnh BF lấy điểm N sao cho AM/AC = BN/BF = k. Tìm k để MN // DE.

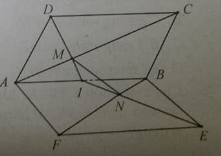
Trong các phát biểu sau đây, phát biểu nào sai?

Cho hai đường thẳng trong không gian không có điểm chung, khẳng định nào sau đây là đúng?

Cho hai đường thẳng a và b cắt nhau. Đường thẳng c song song với a. khẳng định nào sau đây là đúng?

Cho hình hộp ABCD.EFHG, khẳng định nào sau đây là sai?

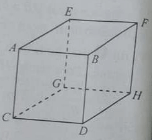
Cho hình chóp S. ABCD, đáy là hình bình hành ABCD, điểm N thuộc cạnh SC sao cho 2NC = NS, M là trọng tâm của tam giác CBD. Phát biểu nào sau đây là đúng?

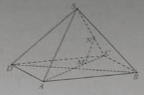
Ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt. khẳng định nào sau đây là đúng?

Cho tứ giác ABCD và các điểm M, N phân biệt thuộc cạnh AB, các điểm P, Q phân biệt thuộc cạnh CD. Phát biểu nào sau đây là đúng?

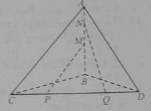
Cho tứ diện ABCD, M, N, P, Q, R, S lần lượt là trung điểm của AB, CD, BC, AD, BD, AC. Phát biểu nào sau đây là sai?

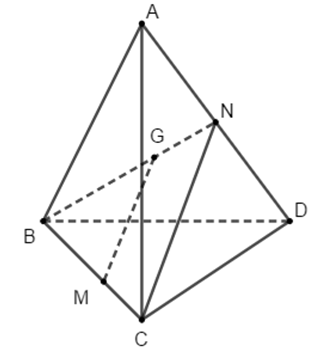
Cho tứ diện ABCD, G là trọng tâm tam giác ABD, N là trung điểm của AD, M là trung điểm trên cạnh BC sao cho MB = 2MC. Khẳng định nào sau đây là đúng?

Giả sử có ba đường thẳng a, b, c trong đó b // a và c //a. những phát biểu nào sau đây là sai?

(1) Nếu mặt phẳng (a, b) không trùng với mặt phẳng (a, c) thì b và c chéo nhau.

(2) Nếu mặt phẳng (a,b) trùng với mặt phẳng (a, c) thì ba đường thẳng a, b, c song song với nhau từng đôi một.

(3) Dù cho hai mặt phẳng (a, b) và (a, c) có trùng nhau hay không, ta vẫn có b // c.

Cho hai đường thẳng a và b chéo nhau. Xét hai đường thẳng p, q mà mà mỗi đường đều cắt cả a và b. Trường hợp nào sau đây không thể xảy ra.

Cho hai đường thẳng a và b chéo nhau. Những phát biểu nào sau đây là sai?

(1) tồn tại hai đường thẳng c, d song song với nhau, mỗi đường đều cắt cả a và b.

(2) không thể tồn tại hai đường thẳng c, d phân biệt, mỗi đường đều cắt cả a và b.

(3) không thể tồn tại một đường thẳng cắt cả a và b.

Cho hình chóp S. ABCD với đáy ABCD là hình bình hành. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh SA, SB, SC, SD. Đường thẳng nào sau đây không song song với đường thẳng MN?

Giả sử (P) , (Q), (R) là ba mặt phẳng cắt nhau theo ba giao tuyến phân biệt a, b, c trong đó a = (P) ∩ (R), b = (Q) ∩ (R), c = (P) ∩ (Q). Trong các mệnh đề sau, mệnh đề nào sai?

Cho hình chóp S. ABCD có đáy là một tứ giác lồi. Gọi M và N lần lượt là trọng tâm của tam giác SAB và SAD. Khẳng định nào sau đây là đúng?

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P, Q lần lượt là các điểm nằm trên các cạnh BC, SC, SD, AD sao cho MN//BS, NP//CD, MQ // CD. Những khẳng định nào sau đây là đúng?

1) PQ // SA

(2) PQ // MN

(3) tứ giác MNPQ là hình thang

(4) tứ giác MNPQ là hình bình hành

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của SB.

Gọi (P) là mặt phẳng qua M và song song với SA; BC.

Thiết diện của hình chóp cắt bởi mặt phẳng (P) là :

Cho hình chóp S.ABCD. trên các cạnh AC, SC lấy lần lượt các điểm I, K sao cho:  $\frac{SC}{SK} = \frac{AC}{AI}$

mặt phẳng (α) đi qua IK cắt các đường thẳng AB, AD, SD, SB tại các điểm theo thứ tự là M, N, P, Q. Khẳng định nào sau đây là đúng?

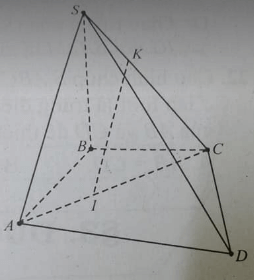
Cho hình chóp S.ABCD đáy ABCD là hình bình hành. Khẳng định nào sau đây là đúng?

Cho hình chóp S.ABCD có đáy là hình bình hành. M là trung điểm của SC. Tìm thiết diện của (MAB) với hình chóp.

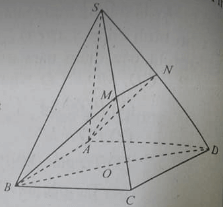
Cho hình chóp S.ABCD có đáy là hình thang với các cạnh đáy là AB, CD. Gọi I, J lần lượt là trung điểm của AD, BC và G là trọng tâm của tam giác SAB. Tìm khẳng định đúng

Cho hình chóp S.ABCD có đáy là hình thang với các cạnh đáy là AB, CD. Gọi I, J lần lượt là trung điểm của AD, BC và G là trọng tâm của tam giác SAB. Tìm điều kiện của AB và CD để thiết diện của (GIJ) với hình chóp S.ABCD là hình bình hành.