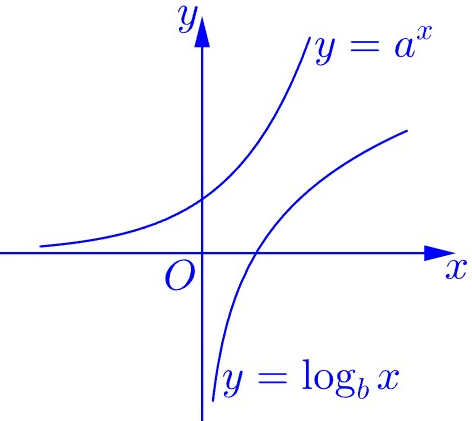
Cho a, b là hai số thực dương khác 1. Đồ thị hai hàm số $y = a^{x}$ và $y = \left(log\right)_{b} x$ được cho như trong hình vẽ bên. Khẳng định nào dưới đây đúng?

Cho dòng điện xoay chiều chạy qua đoạn mạch $AB$ có sơ đồ như hình bên, trong đó $L$ là cuộn cảm thuần và $X$ là đoạn mạch xoay chiều. Khi đó, điện áp giữa hai đầu các đoạn mạch $AN$ và $MB$ có biểu thức lần lượt là $u_{AN}=30\sqrt{2}cos\omega t\left(V\right)$ và $u_{MB}=40\sqrt{2}cos\left(\omega t-\frac{\pi }{2}\right)\left(V\right)$. Điện áp hiệu dụng giữa hai đầu đoạn mạch $\mathrm{A}\mathrm{B}$ có giá trị nhỏ nhất gần nhất với giá trị nào sau đây?

Cho đoạn mạch AB gồm cuộn dây không thuần cảm nối tiếp với tụ điện có điện dung C thay đổi được. Điện áp đặt vào hai đầu mạch có biểu thức $u=U\sqrt{2}\mathrm{c}\mathrm{o}\mathrm{s}(\omega t+\phi )$, trong đó U và ω không đổi. Thay đổi giá trị của C thì nhận thấy, với $C=C_1$ thì điện áp hai đầu tụ điện có giá trị hiệu dụng 40V và trễ pha hơn điện áp giữa hai đầu mạch một góc ${\phi }_1\left(0<{\phi }_1<\mathrm{0,5}\pi \right)$. Khi $C=C_2$ thì dòng điện trong mạch trễ pha hơn so với điện áp hai đầu mạch một góc ${\phi }_1$, điện áp giữa hai đầu tụ khi đó là 20V và mạch tiêu thụ công suất bằng 0,75 công suất cực đại mà nó có thể tiêu thụ. Điện áp hiệu dụng U giữa hai đầu đoạn mạch gần nhất giá trị nào sau đây?

Tiến hành thí nghiệm theo các bước sau:

Bước 1: Cho vào hai bình cầu mỗi bình 10 ml etyl format.

Bước 2: Thêm 10 ml dung dịch H₂SO₄ 20% vào bình thứ nhất, 20 ml dung dịch NaOH 30% vào bình thứ hai.

Bước 3: Lắc đều cả hai bình, lắp ống sinh hàn rồi đun nhẹ trong 5 phút, sau đó để nguội.

Các phát biểu liên quan đến thí nghiệm trên được đưa ra như sau:

a. Kết thúc bước (2), chất lỏng trong hai bình đều phân thành 2 lớp;

b. Ở bước (3), có thể thay việc đun sôi nhẹ bằng cách đun cách thủy (ngâm trong nước nóng);

c. Ở bước (3), trong hai bình đều chứa chất có khả năng tham gia phản ứng tráng bạc.

Số lượng phát biểu đúng là

Thủy phân hoàn toàn chất hữu cơ E (C₉H₁₆O₄, chứa 2 chức este) bằng dung dịch NaOH, thu được sản phẩm gồm ancol X và hai chất hữu cơ Y, Z. Biết Y chứa 3 nguyên tử C và M_X < M_Y > M_Z. Cho Z tác dụng với dung dịch HCl loãng, dư thu được hợp chất hữu cơ T (C₃H₆O₃). Cho các phát biểu sau:

a. Cho a mol T tác dụng với một lượng dư Na thu được a mol H₂;

b. Có 4 công thức cấu tạo thõa mãn tính chất của E;

c. Ancol X là propan-1,2-điol;

d. Khối lượng mol của Z là 96 g/mol.

Số lượng phát biểu đúng là

Các thao tác cơ bản khi sử dụng đồng hồ đa năng hiện số (hình vẽ) để đo điện áp xoay chiều cỡ 120 V gồm:

a. Nhấn nút ON OFF để bật nguồn của đồng hồ.

b. Cho hai đầu đo của hai dây đo tiếp xúc với hai đầu đoạn mạch cần đo điện áp.

c. Vặn đầu đánh dấu của núm xoay tới chấm có ghi 200, trong vùng ACV.

d. Cắm hai đầu nối của hai dây đo vào hai ổ COM và VW.

e. Chờ cho các chữ số ổn định, đọc trị số của điện áp.

g. Kết thúc các thao tác đo, nhấn nút ON OFF để tắt nguồn của đồng hồ.

Thứ tự đúng các thao tác là

Ở một quần thể thực vật ngẫu phối, alen đột biến a làm cây bị chết từ giai đoạn còn hai lá mầm; alen trội A quy định kiểu hình bình thường. Ở một locut gen khác có alen B quy định hoa màu đỏ trội hoàn toàn so với alen b quy định hoa màu trắng. Hai cặp gen nằm trên hai cặp NST thường phân ly độc lập với nhau. Ở một thế hệ (quần thể F1), người ta nhận thấy có 4% số cây bị chết từ giai đoạn hai lá mầm, 48,96% số cây sống và cho hoa màu đỏ, 47,04% số cây sống và cho hoa màu trắng. Biết quần thể ở trạng thái cân bằng đối với gen quy định màu hoa, không có đột biến mới phát sinh. Theo lý thuyết, tỷ lệ cây thuần chủng về cả hai cặp gen trên ở quần thể trước đó (quần thể P) là:

Một sợi dây đàn hồi dài 1m, có hai đầu cố định được căng ngang. Kích thích cho đầu A của dây dao động với tần số 680Hz thì trên dây có sóng dừng ổn định với A và B là hai nút sóng. Tốc độ truyền sóng trên dây là 340m/s. Trên dây, số điểm dao động với biên độ bằng một nửa biên độ dao động của một bụng sóng là

Cho một mạch điện RLC như hình vẽ. Điện trở R, cuộn cảm thuần có độ tự cảm $L=\frac{\mathrm{0,8}}{\pi }\left(H\right)$, tụ điện có điện dung $C=\frac{{10}^{-4}}{\pi }\left(F\right)$. Điện áp hai đầu đoạn mạch $AB$ là $u=U_{0}cos\left(100\pi t\right)$. Biết điện áp giữa hai điểm $AM$ lệch pha so với điện áp giữa hai đầu $AB$ là $\frac{\pi }{2}$. Điện trở R có giá trị bao nhiêu?

Đoạn mạch AB gồm hai đoạn AM và MB mắc nối tiếp, trong đoạn AM có một cuộn cảm thuần độ tự cảm L mắc nối tiếp với một điện trở thuần R, trong đoạn MB có một điện trở thuần 4R mắc nối tiếp với một tụ điện có điện dung C. Đặt vào hai đầu AB một điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi. Thay đổi L và C sao cho cảm kháng của cuộn dây luôn gấp 5 lần dung kháng của tụ điện. Khi độ lệch pha giữa điện áp hai đầu AM so với điện áp hai đầu AB là lớn nhất thì hệ số công suất của cả mạch AB gần nhất với giá trị nào sau đây?