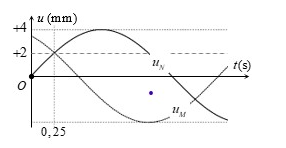
Sóng ngang truyền trên mặt chất lỏng với tốc độ 3 cm/s. Xét hai phần tử M và N nằm trên một phương truyền sóng có vị trí cân bằng cách nhau một khoảng nhỏ hơn bước sóng. Đồ thị biểu diễn li độ sóng của M và N theo thời gian t như hình vẽ. Khoảng cách giữa hai phần tử chất lỏng tại M và N vào thời điểm
s là
A. 61,18 mm.
B. 30,90 mm.
C. 30,59 mm.
D. 61,84 mm.
Đáp án đúng là: C

Sóng ngang truyền trên mặt chất lỏng với tốc độ 3 cm/s. Xét hai phần tử M và N nằm trên một phương truyền sóng có vị trí cân bằng cách nhau một khoảng nhỏ hơn bước sóng. Đồ thị biểu diễn li độ sóng của M và N theo thời gian t như hình vẽ. Khoảng cách giữa hai phần tử chất lỏng tại M và N vào thời điểm s là
61,18 mm.
30,90 mm.
30,59 mm.
61,84 mm.
Đáp án đúng là: C
đến
thì
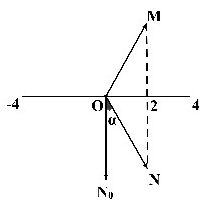
.
Câu hỏi tương tự:
Đề thi chứa câu hỏi này:
1 mã đề 39 câu hỏi 50 phút
6,935 xem517 thi
