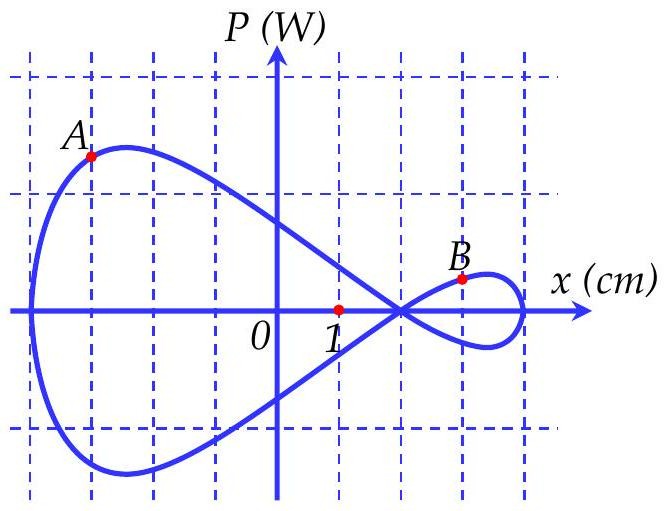
Một con lắc lò xo thẳng đứng dao động điều hòa, hình bên là đồ thị sự phụ thuộc của công suất tức thời của lực đàn hồi lò xo theo li độ x của vật. Chọn $$ t=0 tương ứng là điểm B trên đồ thị. Lấy $$ g=10 m/ s 2 , lấy $$ π 2 =10 , độ cứng lò xo $$ k=100 N/m . Kết luận nào sau đây là đúng?

A.  

Khoảng thời gian trong một chu kỳ dao động có lực đàn hồi và lực kéo về cùng hướng nhau đồng thời cùng hướng chuyển động là $\frac{1}{6\sqrt{2}}\left(s\right)$

B.  

Cơ năng của con lắc lò xo có giá trị là $\mathrm{0,02}\mathrm{J}$

C.  

Thời điểm đầu tiên có được điểm A trên đồ thị là $t\approx \mathrm{0,076}\left(\mathrm{s}\right)$

D.  

Giá trị công suất tức thời tại B là $5\pi \sqrt{14}\left(W\right)$

Đáp án đúng là: A

$W = \dfrac{1}{2} k A^{2} = \dfrac{1}{2} . 100 . 0 , \left(04\right)^{2} = 0 , 08 J \rightarrow$ B sai
$\omega = \sqrt{\dfrac{g}{\Delta l_{0}}} = \sqrt{\dfrac{10}{0 , 02}} = 5 \pi \sqrt{2}$ (rad/s) $\rightarrow T = \dfrac{2 \pi}{\omega} = 0 , 2 \sqrt{2} s$
Khoảng thời điểm đầu tiên có điểm A trên đồ thị: $t = \dfrac{T}{2} = \dfrac{0 , 2 \sqrt{2}}{2} \approx 0 , 14 s \rightarrow$C sai
Tại B: Vật có li độ x = 3 cm, lò xo đang nén $∆l$ = 1cm = 0,01m
$F_{d h} = k . \Delta l = 100 . 0 , 01 = 1 N$ và $v = \omega \sqrt{A^{2} - x^{2}} = 5 \pi \sqrt{2} . \sqrt{4^{2} - 3^{2}} = 5 \pi \sqrt{14} c m / s = 0 , 05 \pi \sqrt{14} m / s$
Công suất tức thời tại B: $P_{B} = F_{d h} v = 0 , 05 \pi \sqrt{14} W \rightarrow$D sai
Lực đàn hồi và lực kéo về cùng hướng nhau đồng thời cùng hướng chuyển động
⇒ vật đi từ biên dưới đến VTCB và vật đi từ trên đến VTTN của lò xo
$\Rightarrow \Delta t = \dfrac{\alpha}{\omega} = \dfrac{\pi / 2 + \pi / 3}{5 \pi \sqrt{2}} = \dfrac{1}{6 \sqrt{2}} s$. Chọn A