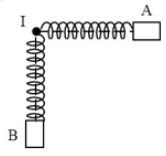
Trên mặt phẳng nhẵn nằm ngang có hai con lắc lò xo, các lò xo có cùng độ cứng
. Các vật nhỏ
và
có khối lượng lần lượt là
và
. Ban đầu,
và
được giữ ở hai vị trí sao cho hai lò xo đều giãn 5 cm. Đồng thời thả nhẹ để hai vật dao động điều hòa trên hai đường thẳng vuông góc với nhau đi qua giá
cố định (hình vẽ). Trong quá trình hệ dao động, lực đàn hồi do các lò xo tác dụng lên giá
có độ lớn cực tiểu là
A.
.
B.
.
C.
.
D.
.
Đáp án đúng là: C

.
.
.
.
Đáp án đúng là: C
và
(N)
và
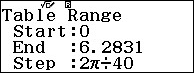

Để tìm giá trị chính xác ta shift solve đạo hàm với nghiệm xấp xỉ là 0,9424
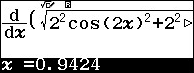
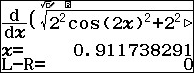
xóa dấu đạo hàm và calc để tìm giá trị chính xác
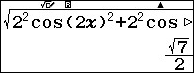
Câu hỏi tương tự:
Đề thi chứa câu hỏi này:
1 mã đề 40 câu hỏi 50 phút
1,956 xem137 thi
