Trang chủ Đề thi [2020] Bộ GD&ĐT mã đề 103 - Đề thi tốt nghiệp THPT môn Toán năm 2020
thumbnail

[2020] Bộ GD&ĐT mã đề 103 - Đề thi tốt nghiệp THPT môn Toán năm 2020

Thời gian làm bài: 1 giờ

Đề thi nằm trong bộ sưu tập: 📘 Tuyển Tập Bộ 500 Đề Thi Ôn Luyện Môn Toán THPT Quốc Gia Các Tỉnh Từ Năm 2018-2025 - Có Đáp Án Chi Tiết


Bạn chưa làm đề thi này!!!

Hãy bắt đầu chinh phục nào!



 

Xem trước nội dung:

Câu 1: 1 điểm

Cho hình trụ có bán kính đáy r = 5 và độ dài đường sinh l = 3 . Diện tích xung quanh của hình trụ đã cho bằng

A.  
15π15\pi
B.  
25π25\pi
C.  
30π30\pi
D.  
75π75\pi
Câu 2: 1 điểm

Cho khối nón có bán kính đáy r = 2, chiều cao h = 5 Thể tích của khối nón đã cho bằng

A.  
20π3\frac{{20\pi }}{3}
B.  
20π20\pi
C.  
10π3\frac{{10\pi }}{3}
D.  
10π10\pi
Câu 3: 1 điểm

Biết ∫12f(x)dx=2.\int_1^2 f (x)dx = 2. Giá trị của int123f(x)dxint_1^2 3 f(x)dx bằng

A.  
5
B.  
6
C.  
2/3
D.  
8
Câu 4: 1 điểm

Trong không gian Oxyz, cho đường thẳng d:x−34=y+1−2=z+23.d:\frac{{x - 3}}{4} = \frac{{y + 1}}{{ - 2}} = \frac{{z + 2}}{3}. Vectơ nào dưới đây là một vectơ chỉ phương của d?

A.  
u⃗3=(3;−1;−2){\vec u_3} = (3; - 1; - 2)
B.  
u4→=(4;2;3)\overrightarrow {{u_4}} = (4;2;3)
C.  
u2→=(4;−2;3)\overrightarrow {{u_2}} = (4; - 2;3)
D.  
u⃗1=(3;1;2){\vec u_1} = (3;1;2)
Câu 5: 1 điểm

Cho khối cầu có bán kính r = 2 Thể tích của khối cầu đã cho bằng

A.  
16π16\pi
B.  
32π3\frac{{32\pi }}{3}
C.  
32π32\pi
D.  
8π3\frac{{8\pi }}{3}
Câu 6: 1 điểm

Trong không gian Oxyz, hình chiếu vuông góc của điểm A(3;5;1) trên trục Ox có tọa độ là

A.  
(0;5;2)
B.  
(0;5;0)
C.  
(3;0;0)
D.  
(0;02)
Câu 7: 1 điểm

Nghiệm của phương trình log⁡2(x−2)=3{\log _2}(x - 2) = 3 là

A.  
x = 6
B.  
x = 8
C.  
x = 11
D.  
x = 10
Câu 8: 1 điểm

Cho hàm số f(x) có bảng biến thiên như sau:

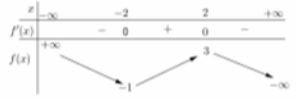
Giá trị cực tiểu của hàm số đã cho bằng

A.  
2
B.  
-2
C.  
3
D.  
-1
Câu 9: 1 điểm

Trong không gian Oxyz, cho 3 điểm A(−1;0,0),B(0;2;0)A( - 1;0,0),B(0;2;0) và C(0;0;3).C(0;0;3). Mặt phẳng (ABC) có phương trình là

A.  
x1+y2+z−3=1\frac{x}{1} + \frac{y}{2} + \frac{z}{{ - 3}} = 1
B.  
x1+y−2+z3=1\frac{x}{1} + \frac{y}{{ - 2}} + \frac{z}{3} = 1
C.  
x−1+y2+z3=1.\frac{x}{{ - 1}} + \frac{y}{2} + \frac{z}{3} = 1.
D.  
x1+y2+z3=1\frac{x}{1} + \frac{y}{2} + \frac{z}{3} = 1
Câu 10: 1 điểm

Nghiệm của phương trình 3x+1=9{3^{x + 1}} = 9 là

A.  
x = 1
B.  
x = 2
C.  
x = -2
D.  
x = -1
Câu 11: 1 điểm

Cho khối hộp chữ nhật có ba kích thước 2; 6; 7. Thể tích của khối hộp đã cho bằng

A.  
28
B.  
14
C.  
15
D.  
84
Câu 12: 1 điểm

Cho khối chóp có diện tích đáy B = 2 và chiều cao h = 3 Thể tích của khối chóp bằng

A.  
12
B.  
2
C.  
3
D.  
6
Câu 13: 1 điểm

Số phức liên hợp của số phức z=2−5iz = 2 - 5i là

A.  
zˉ=2+5i\bar z = 2 + 5i
B.  
zˉ=−2+5i\bar z = - 2 + 5i
C.  
zˉ=2−5i\bar z = 2 - 5i
D.  
zˉ=−2−5i\bar z = - 2 - 5i
Câu 14: 1 điểm

Cho cấp số nhân (un)\left( {{u_n}} \right) với u1=3{u_1} = 3 và công bội q = 4 Giá trị của u2{u_2} bằng

A.  
64
B.  
81
C.  
12
D.  
3/4
Câu 15: 1 điểm

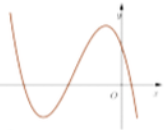
Cho hàm số bậc ba y = f(x) có đồ thị là đường cong trong hình bên

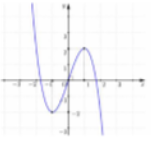
Số nghiệm thực của phương trình f(x) = 1 là

A.  
1
B.  
0
C.  
2
D.  
3
Câu 16: 1 điểm

Cho hai số phức z1=1−2i{z_1} = 1 - 2i và z2=2+i.{z_2} = 2 + i. Số phức z1+z2{z_1} + {z_2} bằng

A.  
3 + i
B.  
-3 - i
C.  
3 - i
D.  
-3 + i
Câu 17: 1 điểm

Cho hàm số f(x) có bảng biến thiên như sau:

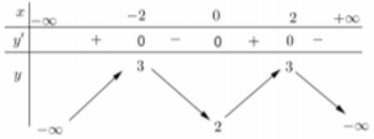
Hàm số đã cho đồng biến trên khoảng nào dưới đây?

A.  
(-2;2).
B.  
(0; 2).
C.  
(-2,0)
D.  
(2;+∞)(2; + \infty )
Câu 18: 1 điểm

Tiệm cận ngang của đồ thị hàm số y=2x+1x−1y = \frac{{2x + 1}}{{x - 1}} là

A.  
y=12y = \frac{1}{2}
B.  
y = - 1
C.  
y = 1
D.  
y = 2
Câu 19: 1 điểm

Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?

A.  
y=−x4+2x2y = - {x^4} + 2{x^2}
B.  
y=x3−3x2y = {x^3} - 3{x^2}
C.  
y=x4−2x2y = {x^4} - 2{x^2}
D.  
y=−x3+3x2y = - {x^3} + 3{x^2}
Câu 20: 1 điểm

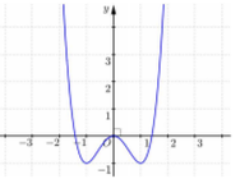
Trong không gian Oxyz, cho mặt cầu (S):x2+y2+(z−1)2=16.(S):{x^2} + {y^2} + {(z - 1)^2} = 16. Bán kính của (S) bằng

A.  
32
B.  
8
C.  
4
D.  
16
Câu 21: 1 điểm

Trong mặt phẳng tọa độ, biết điểm M(-2,1) là điểm biểu diễn số phức z. Phần thực của z bằng

A.  
-2
B.  
2
C.  
1
D.  
-1
Câu 22: 1 điểm

Tập xác định của hàm số y=log⁡3xy = {\log _3}x là

A.  
(−∞;0)( - \infty ;0)
B.  
(0;+∞)(0; + \infty )
C.  
(−∞;+∞)( - \infty ; + \infty )
D.  
[0;+∞)[0; + \infty )
Câu 23: 1 điểm

Có bao nhiêu cách xếp 5 học sinh thành một hàng dọc?

A.  
1
B.  
25
C.  
5
D.  
120
Câu 24: 1 điểm

Với a,b là các số thực dương tùy ý và ae1,log⁡a3ba e 1,{\log _{{a^3}}}b bằng

A.  
3+log⁡ab3 + {\log _a}b
B.  
3log⁡ab3{\log _a}b
C.  
13+log⁡b\frac{1}{3} + \log b
D.  
13log⁡ab\frac{1}{3}{\log _a}b
Câu 25: 1 điểm

∫x4dx\int {{x^4}} dx bằng

A.  
15x5+C\frac{1}{5}{x^5} + C
B.  
4x3+C4{x^3} + C
C.  
x5+C{x^5} + C
D.  
5x5+C5{x^5} + C
Câu 26: 1 điểm

Biết F(x)=x3F(x) = {x^3} là một nguyên hàm của hàm số f(x) trên . Giá trị của ∫13(1+f(x))dx\int_1^3 {(1 + f(} x))dx bằng

A.  
20
B.  
22
C.  
26
D.  
28
Câu 27: 1 điểm

Cho hình nón có bán kính đáy bằng 3 và góc ở đỉnh bằng 60o. Diện tích xung quanh của hình nón đã cho bằng

A.  
18π18\pi
B.  
36π36\pi
C.  
63π6\sqrt 3 \pi
D.  
123π12\sqrt 3 \pi
Câu 28: 1 điểm

Diện tích hình phẳng giới hạn bởi hai đường y=x2−2y = {x^2} - 2 và y=3x−2y = 3x - 2 bằng

A.  
92\frac{9}{2}
B.  
9π2\frac{{9\pi }}{2}
C.  
1256\frac{{125}}{6}
D.  
125π6\frac{{125\pi }}{6}
Câu 29: 1 điểm

Tập nghiệm của bất phương trình 2x2−7<4{2^{{x^2} - 7}} < 4 là

A.  
(-3,3)
B.  
(0,3)
C.  
(−∞;3)( - \infty ;3)
D.  
(3;+∞)(3; + \infty )
Câu 30: 1 điểm

Cho a và b là hai số thực dương thỏa mãn 9log⁡3(ab)=4a{9^{{{\log }_3}\left( {ab} \right)}} = 4a . Giá trị của ab2a{b^2} bằng

A.  
3
B.  
6
C.  
2
D.  
4
Câu 31: 1 điểm

Trong không gian Oxyz, cho điểm M(2;−1;2)M(2; - 1;2) và đường thẳng d:x−12=y+23=z−31.d:\frac{{x - 1}}{2} = \frac{{y + 2}}{3} = \frac{{z - 3}}{1}. Mặt phẳng đi qua điểm M và vuông góc với d có phương trình là

A.  
2x + 3y + z - 3 = 0
B.  
2x - y + 2z - 9 = 0
C.  
2x + 3y + z + 3 = 0
D.  
2x - y + 2z + 9 = 0
Câu 32: 1 điểm

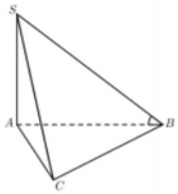
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB=a,BC=3a;SAAB = a,BC = 3a;SA vuông góc với mặt phẳng đáy và SA=30aSA = \sqrt {30} a (tham khảo hình bên). Góc giữa đường thẳng SC và mặt phẳng đáy bằng

A.  
45
B.  
90
C.  
60
D.  
30
Câu 33: 1 điểm

Cho z0{z_0} là nghiệm phức có phần ảo dương của phương trình z2+4z+13=0.{z^2} + 4z + 13 = 0. Trên mặt phẳng toa độ, điểm biểu diễn của số phức 1−z01 - {z_0} là

A.  
P( - 1; - 3)
B.  
M( - 1;3)
C.  
N(3; - 3)
D.  
Q(3;3)
Câu 34: 1 điểm

Trong không gian Oxyz, cho ba điểm A(1;2;0),B(1;1;2)A(1;2;0),B(1;1;2) và C(2;3;1)C(2;3;1) . Đường thẳng đi qua A và song song với BC có phương trình là

A.  
x−11=y−22=z−1\frac{{x - 1}}{1} = \frac{{y - 2}}{2} = \frac{z}{{ - 1}}
B.  
x−13=y−24=z3\frac{{x - 1}}{3} = \frac{{y - 2}}{4} = \frac{z}{3}
C.  
x+13=y+24=z3\frac{{x + 1}}{3} = \frac{{y + 2}}{4} = \frac{z}{3}
D.  
x+11=y+22=z−1\frac{{x + 1}}{1} = \frac{{y + 2}}{2} = \frac{z}{{ - 1}}
Câu 35: 1 điểm

Giá trị nhỏ nhất của hàm số f(x)=x3−30xf(x) = {x^3} - 30x trên đoạn [2; 19] bằng

A.  
201020\sqrt {10}
B.  
-63
C.  
−2010 - 20\sqrt {10}
D.  
-52
Câu 36: 1 điểm

Cho hàm số f(x) liên tục trên R và có bảng xét dấu của f(x) như sau:

Số điểm cực trị của hàm số đã cho là

A.  
2
B.  
4
C.  
3
D.  
1
Câu 37: 1 điểm

Cho hai số phức z=4+2iz = 4 + 2i và w=1+iw = 1 + i . Modun của số phức z.wˉz.\bar w bằng

A.  
222\sqrt 2
B.  
8
C.  
2102\sqrt {10}
D.  
40
Câu 38: 1 điểm

Số giao điểm của đồ thị hàm số y=x3+x2y = {x^3} + {x^2} và đồ thị hàm số y=x2+5xy = {x^2} + 5x là

A.  
3
B.  
0
C.  
1
D.  
2
Câu 39: 1 điểm

Trong năm 2019, diện tích rừng trồng mới của tỉnh A là 900 ha. Giả sử diện tích rừng trồng mới của tỉnh A mỗi năm tiếp theo đều tăng 6% so với diện tích rừng trồng mới của năm liền trước. Kể từ sau năm 2019, năm nào dưới đây là năm đầu tiên tỉnh A có diện tích rừng trồng mới trong năm đó đạt trên 1700 ha?

A.  
Năm 2029
B.  
Năm 2051.
C.  
Năm 2030.
D.  
Năm 2050.
Câu 40: 1 điểm

Cho hình chóp S.ABC có đáy là tam giác đều cạnh 2a, SA vuông góc với mặt phẳng đáy, góc giữa mặt phẳng (SBC) và mặt phẳng đáy bằng 60o. Diện tích của mặt cầu ngoại tiếp hình chóp S.ABC bằng

A.  
43πa23\frac{{43\pi {a^2}}}{3}
B.  
19πa23\frac{{19\pi {a^2}}}{3}
C.  
43πa29\frac{{43\pi {a^2}}}{9}
D.  
21πa221\pi {a^2}
Câu 41: 1 điểm

Tập hợp tất cả các giá trị thực của tham số m để hàm số y=x+2x+my = \frac{{x + 2}}{{x + m}} đồng biến trên khoảng (−∞;−5)( - \infty ; - 5) là

A.  
(2;5]
B.  
[2;5)
C.  
[2; + \infty )
D.  
(2;5)
Câu 42: 1 điểm

Cho hàm số f(x)=xx2+1⋅f(x) = \frac{x}{{\sqrt {{x^2} + 1} }} \cdot

Họ tất cả các nguyên hàm của hàm số g(x)=(x+1)f′(x)g(x) = (x + 1)f'(x) là

A.  
x2+2x−12x2+1+C\frac{{{x^2} + 2x - 1}}{{2\sqrt {{x^2} + 1} }} + C
B.  
x+12x2+1+C\frac{{x + 1}}{{2\sqrt {{x^2} + 1} }} + C
C.  
2x2+x+1x2+1+C\frac{{2{x^2} + x + 1}}{{\sqrt {{x^2} + 1} }} + C
D.  
x−1x2+1+C\frac{{x - 1}}{{\sqrt {{x^2} + 1} }} + C
Câu 43: 1 điểm

Gọi S là tập hợp tất cả các số tự nhiên có 4 chữ số đôi một khác nhau và các chữ số thuộc tập hợp {1,2,3,4,5,6,7}.\{ 1,2,3,4,5,6,7\} . Chọn ngẫu nhiên một số thuộc S, xác suất để số đó không có hai chữ số liên tiếp nào cùng chẵn bằng

A.  
935\frac{9}{{35}}
B.  
1635\frac{{16}}{{35}}
C.  
2235\frac{{22}}{{35}}
D.  
1935\frac{{19}}{{35}}
Câu 44: 1 điểm

Cho hàm số bậc bốn f(x) có bảng biến thiên như sau:

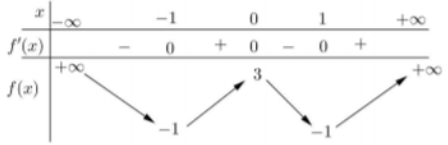
Số điểm cực trị của hàm số g(x)=x4[f(x−1)]2g(x) = {x^4}{[f(x - 1)]^2} là

A.  
7
B.  
5
C.  
9
D.  
11
Câu 45: 1 điểm

Xét các số thực không âm x và y thỏa mãn 2x+y.4x+y−1≥32x + y{.4^{x + y - 1}} \ge 3 . Giá trị nhỏ nhất của biểu thức P=x2+y2+2x+4yP = {x^2} + {y^2} + 2x + 4y bằng

A.  
338\frac{{33}}{8}
B.  
98\frac{9}{8}
C.  
214\frac{{21}}{4}
D.  
418\frac{{41}}{8}
Câu 46: 1 điểm

Cho hàm số có đồ thị là đường cong trong hình bên. Có bao nhiêu số dương trong các số a, b, c, d?

A.  
4
B.  
2
C.  
1
D.  
3
Câu 47: 1 điểm

Cho hình chóp đều S.ABCD có cạnh đáy bằng a, cạnh bên bằng a2a\sqrt 2 và O là tâm của đáy. Gọi M, N, P, Q lần lượt là các điểm đối xứng với O qua trọng tâm của các tam giác SAB, SBC, SCD, SDA và S' là điểm đối xứng của S qua O. Thể tích của khối chóp S'.MNPQ bằng

A.  
269a3\frac{{2\sqrt 6 }}{9}{a^3}
B.  
40681a3\frac{{40\sqrt 6 }}{{81}}{a^3}
C.  
10681a3\frac{{10\sqrt 6 }}{{81}}{a^3}
D.  
20681a3\frac{{20\sqrt 6 }}{{81}}{a^3}
Câu 48: 1 điểm

Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác đều cạnh a và AA' = 2a. Gọi M là trung điểm của AA' (tham khảo hình bên). Khoảng cách từ M đến mặt phẳng (AB'C) bằng

A.  
57a19\frac{{\sqrt {57} a}}{{19}}
B.  
5a5\frac{{\sqrt 5 a}}{5}
C.  
25a5\frac{{2\sqrt 5 a}}{5}
D.  
257a19\frac{{2\sqrt {57} a}}{{19}}
Câu 49: 1 điểm

Có bao nhiêu số nguyên x sao cho ứng với mỗi x có không quá 127 số nguyên y thỏa mãn {\log _3}\left( {{x^2} + y} \right) \ge {\log _2}(x + y)?

A.  
89
B.  
46
C.  
45
D.  
90
Câu 50: 1 điểm

Cho hàm số bậc bốn y = f(x) có đồ thị là đường cong trong hình bên.

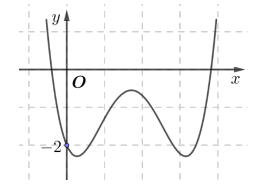
Số nghiệm thực phân biệt của phương trình f(x2f(x))+2=0f\left( {{x^2}f(x)} \right) + 2 = 0 là

A.  
8
B.  
12
C.  
6
D.  
9

Xem thêm đề thi tương tự

thumbnail
[2020] Bộ GD&ĐT - Mã đề 421 - Đề thi tốt nghiệp THPT năm 2020 môn Tiếng Anh
Chưa có mô tả

50 câu hỏi 1 mã đề 1 giờ

209,304 lượt xem 112,700 lượt làm bài

Bạn chưa chinh phục đề thi này!!!
thumbnail
[2020] Bộ GD&ĐT mã đề 213 - Đề thi tốt nghiệp THPT môn Sinh học năm 2020
Chưa có mô tả

40 câu hỏi 1 mã đề 1 giờ

207,774 lượt xem 111,874 lượt làm bài

Bạn chưa chinh phục đề thi này!!!
thumbnail
[2020] Bộ GD&ĐT mã đề 217 - Đề thi tốt nghiệp THPT môn Hóa học năm 2020
Chưa có mô tả

40 câu hỏi 1 mã đề 1 giờ

204,195 lượt xem 109,949 lượt làm bài

Bạn chưa chinh phục đề thi này!!!
thumbnail
[2020] Bộ GD&ĐT mã đề 202 - Đề thi tốt nghiệp THPT môn Hóa học năm 2020
Chưa có mô tả

40 câu hỏi 1 mã đề 1 giờ

197,955 lượt xem 106,589 lượt làm bài

Bạn chưa chinh phục đề thi này!!!
thumbnail
[2020] Bộ GD&ĐT mã đề 224 - Đề thi tốt nghiệp THPT môn Hóa học năm 2020
Chưa có mô tả

40 câu hỏi 1 mã đề 1 giờ

207,160 lượt xem 111,545 lượt làm bài

Bạn chưa chinh phục đề thi này!!!
thumbnail
[2020] Bộ GD&ĐT mã đề 205 - Đề thi tốt nghiệp THPT môn Hóa học năm 2020
Chưa có mô tả

40 câu hỏi 1 mã đề 1 giờ

207,290 lượt xem 111,615 lượt làm bài

Bạn chưa chinh phục đề thi này!!!
thumbnail
[2020] Bộ GD&ĐT mã đề 204 - Đề thi tốt nghiệp THPT môn Sinh học năm 2020
Chưa có mô tả

40 câu hỏi 1 mã đề 1 giờ

214,010 lượt xem 115,234 lượt làm bài

Bạn chưa chinh phục đề thi này!!!
thumbnail
[2020] Bộ GD&ĐT - Đề thi tốt nghiệp THPT năm 2020 môn Vật lý mã đề 203
Chưa có mô tả

40 câu hỏi 1 mã đề 1 giờ

206,445 lượt xem 111,160 lượt làm bài

Bạn chưa chinh phục đề thi này!!!
thumbnail
Đề Thi Minh Hoạ THPT Quốc Gia Môn Tiếng Anh Năm 2020 - Bộ GD&ĐT (Có Đáp Án)THPT Quốc giaTiếng Anh

Luyện thi tốt nghiệp THPT Quốc gia môn Tiếng Anh năm 2020 với đề thi minh họa do Bộ GD&ĐT phát hành. Đề thi bám sát cấu trúc chính thức của kỳ thi, bao gồm các câu hỏi về ngữ pháp, từ vựng, kỹ năng đọc hiểu và giao tiếp tiếng Anh, kèm đáp án chi tiết giúp học sinh lớp 12 củng cố kiến thức và chuẩn bị tốt nhất cho kỳ thi THPT Quốc gia. Đây là tài liệu ôn tập hữu ích giúp học sinh đạt kết quả cao. Thi thử trực tuyến miễn phí và tiện lợi.

50 câu hỏi 1 mã đề 50 phút

103,045 lượt xem 55,475 lượt làm bài

Bạn chưa chinh phục đề thi này!!!