[2021] Trường THPT Phú Nhuận lần 2 - Đề thi thử THPT QG năm 2021 môn Toán

Có bao nhiêu cách chọn 3 học sinh từ một nhóm gồm 7 học sinh.

Cho cấp số cộng $\left( {{u}_{n}} \right)$ có ${{u}_{1}}=2$ và ${{u}_{5}}=18$ . Giá trị của ${{u}_{3}}$ bằng

Cho hàm số $f(x)$ có bảng biến thiên như sau:

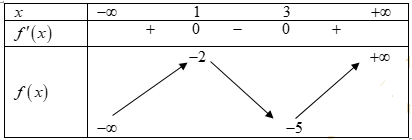
Hàm số đã cho đồng biến trên khoảng nào, trong các khoảng đã cho dưới đây?

Cho hàm số f(x) có bảng biến thiên như sau:

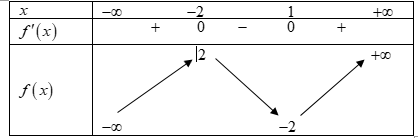
Điềm cực tiểu của hàm số đã cho là:

Cho hàm số f(x) có bảng xét dấu của đạo hàm ${{f}^{\prime }}(x)$ như sau:

Hàm số f(x) có bao nhiêu điềm cực trị?

Tiệm cận đứng của đồ thị hàm số $y=\frac{x+2}{2-x}$ là đường thẳng:

Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?

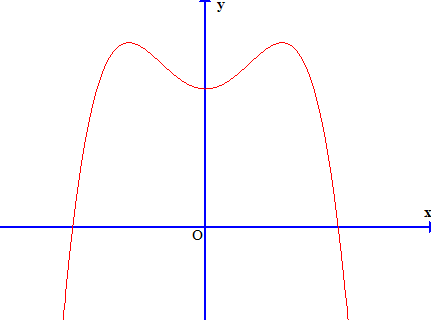
Đồ thị của hàm số $y={{x}^{3}}-3x+2$ cắt trục hoành tại điểm có hoành độ bằng

Với a là số thực dương tùy ý, ${{\log }_{4}}\left( 16a \right)$ bằng

Đạo hàm của hàm số $y={{4}^{x}}$ là:

Với a là số thực dương tùy ý $\sqrt[3]{{{a^9}}}$ bằng

Nghiệm của phương trình ${3^{4x - 12}} = 81$ là:

Nghiệm của phương trình ${\log _4}\left( {4x} \right) = 2$ là:

Cho hàm số $f\left( x \right)=5{{x}^{4}}+1$ . Trong các khẳng định sau, khẳng định nào đúng?

Cho hàm số $f\left( x \right)=\cos 3x$ . Trong các khẳng định sau, khẳng định nào đúng?

Nếu $\int_{-1}^{2}{f}\left( x \right)\text{d}x=2$ và $\int_{2}^{5}{f}\left( x \right)\text{d}x=-3$ thì $\int_{-1}^{5}{f}\left( x \right)\text{d}x$ bằng

Tích phân $\int_0^2 {{x^5}} \;dx$ bằng

Số phức liên hợp của số phức z = 6 - 7i là:

Cho hai số phức z=2+i và w=3+2i. Số phức z-w bằng

Trên mặt phẳng tọa độ, điểm biểu diễn số phức $4+\sqrt{3}i$ có tọa độ là

Một khối chóp có diện tích đáy bằng 18 và chiều cao bằng 12. Thể tích của khối chóp đó bằng

Thể tích của khối hộp chữ nhật có ba kích thước 5; 8; 6 bằng

Công thức tính thể tích V của khối nón có bán kính đáy r và chiều cao 3h là:

Một hình trụ có bán kính đáy $r=8\,cm$ và độ dài đường sinh $l=5\,cm.$ Diện tích xung quanh của hình trụ đó bằng

Trong không gian Oxyz, cho hai điểm $A\left( 0;1;-2 \right)$ và $B\left( 6;1;0 \right).$ Trung điểm của đoạn thẳng AB có tọa độ là

Trong không gian Oxyz, mặt cầu $\left( S \right):{{\left( x+2 \right)}^{2}}+{{\left( y-1 \right)}^{2}}+{{z}^{2}}=16$ có bán kính bằng

Trong không gian Oxyz, mặt phẳng nào dưới đây đi qua điểm $M\left( 3;-1;0 \right)$ ?

Trong không gian Oxyz, vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng đi qua gốc tọa độ O và điểm $M\left( -1;3;2 \right)$ ?

Chọn ngẫu nhiên một số trong 21 số nguyên dương đầu tiên. Xác suất để chọn được số chẵn bằng

Hàm số nào dưới đây nghịch biến trên $\mathbb{R}$ ?

Cho hàm số $f\left( x \right)={{x}^{4}}-2{{x}^{2}}-2.$ Kí hiệu $M=\underset{x\in \left[ 0;2 \right]}{\mathop{\max }}\,f\left( x \right), m=\underset{x\in \left[ 0;2 \right]}{\mathop{\min }}\,f\left( x \right).$ Khi đó M-m bằng

Tập nghiệm của bất phương trình ${\left( {\frac{1}{3}} \right)^{ - 3{x^2}}} < {3^{2x + 1}}$ là

Nếu $\int\limits_{0}^{2}{\left[ 2f\left( x \right)+x \right]dx=5}$ thì $\int\limits_{0}^{2}{f\left( x \right)dx}$ bằng

Cho số phức z=2-i. Môđun của số phức $\left( 1+i \right)z$ bằng

Cho khối lăng trụ đứng $ABC.{A}'{B}'{C}'$ có ${B}'B=a$ , đáy ABC là tam giác vuông cân tại B và $AC=a\sqrt{3}$ . Góc giữa ${C}'A$ và mp $\left( ABC \right)$ bằng

Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và cạnh bên tạo với đáy một góc $60{}^\circ$ . Khoảng cách từ S đến mặt phẳng $\left( ABCD \right)$ bằng

Trong không gian với hệ tọa độ Oxyz, mặt cầu có tâm $I\left( -1;\,\,2;\,\,0 \right)$ và đi qua điểm $M\left( 2;6;0 \right)$ có phương trình là:

Trong không gian Oxyz, đường thẳng đi qua hai điểm $A\left( 2;\,3;\,-1 \right),B\left( 1;\,2;\,4 \right)$ có phương trình tham số là:

Cho hàm số $y=f\left( x \right)$ có đạo hàm ${f}'\left( x \right)$ . Hàm số $y={f}'\left( x \right)$ liên tục trên tập số thực $\mathbb{R}$ và có đồ thị như hình vẽ.

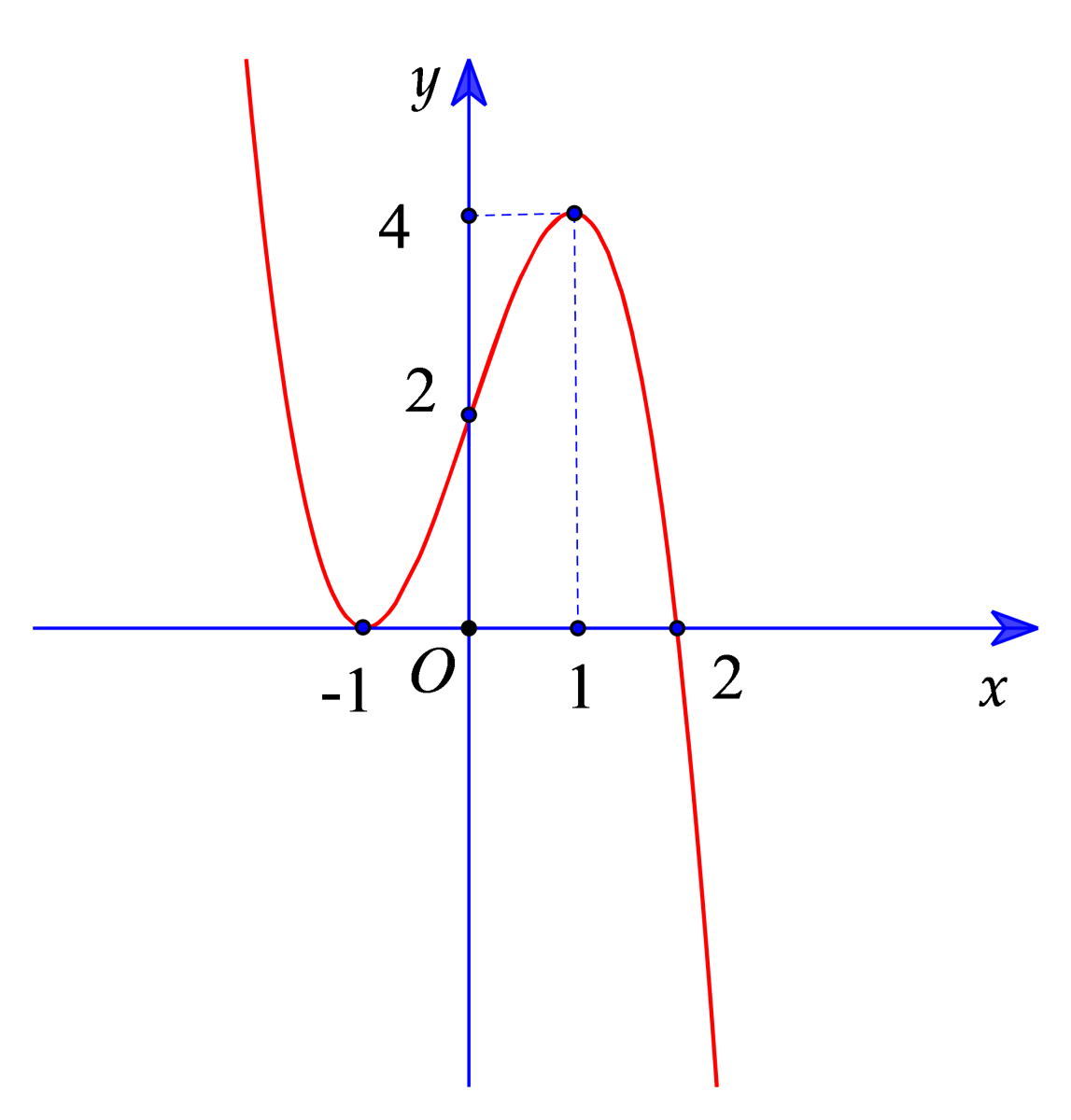
Biết $f\left( -1 \right)=\frac{13}{4},\,f\left( 2 \right)=6$ . Giá trị nhỏ nhất của hàm số $g\left( x \right)={{f}^{3}}\left( x \right)-3f\left( x \right)$ trên $\left[ -1;2 \right]$ bằng

Có bao nhiêu số nguyên dương y sao cho ứng với mỗi y có không quá 5 số nguyên x thỏa mãn $\left( {{3}^{x+1}}-\sqrt{3} \right)\left( {{3}^{x}}-y \right)<0?$

Cho hàm số $f\left( x \right) = \left\{ \begin{array}{l}4x - \sqrt {4x + 9} \,\,\,{\rm{khi}}\,\,x > 0\\4a + {\tan ^2}\,x\,\,\,\,\,\,\,\,{\rm{khi}}\,\,x \le 0\end{array} \right.$ , đồng thời $I = \int\limits_{ - \frac{\pi }{4}}^4 {f\left( x \right)dx} = \frac{{50}}{3}$ . Tính a.

Tính môđun của số phức z thỏa mãn $\left( 1+i \right).z.\left| z \right|-1=\left( i-2 \right)\left| z \right|$ và $\left| z \right|$ là một số nguyên

Cho hình chóp S.ABC là tam giác vuông tại A, $\widehat{ABC}=30{}^\circ$ , BC=a. Hai mặt bên $\left( SAB \right)$ và $\left( SAC \right)$ cùng vuông góc với đáy $\left( ABC \right)$ , mặt bên $\left( SBC \right)$ tạo với đáy một góc $45{}^\circ$ . Thể tích của khối chóp $S.ABC$ là

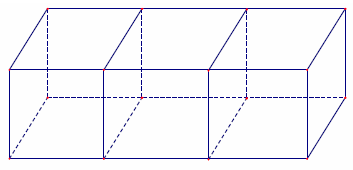
Một người xây nhà xưởng hình hộp chữ nhật có diện tích mặt sàn là $1152{{\rm{m}}^{\rm{2}}}$ và chiều cao cố định. Người đó xây các bức tường xung quanh và bên trong để ngăn nhà xưởng thành ba phòng hình chữ nhật có kích thước như nhau (không kể trần nhà). Vậy cần phải xây các phòng theo kích thước nào để tiết kiệm chi phí nhất (bỏ qua độ dày các bức tường).

Trong không gian với hệ tọa độ Oxy, gọi d đi qua $A\left( 3;-1;1 \right)$ , nằm trong mặt phẳng $\left( P \right):x-y+z-5=0$ , đồng thời tạo với $\Delta :\frac{x}{1}=\frac{y-2}{2}=\frac{z}{2}$ một góc $45{}^\circ$ . Phương trình đường thẳng d là

Cho hàm số $y=f\left( x \right)$ có đồ thị như hình vẽ.

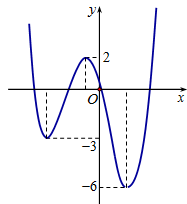
Gọi S là tập hợp các giá trị nguyên dương của tham số m để hàm số $y=\left| f\left( x-1 \right)+m \right|$ có 5 điểm cực trị. Tổng giá trị tất cả các phần tử của S bằng

Có bao nhiêu cặp số $\left( x;\,y \right)$ thỏa mãn tính chất ${{\left( {{\log }_{y}}x \right)}^{2021}}={{\log }_{y}}{{x}^{2021}}$ , ở đó x là số thực dương, y là số nguyên dương nhỏ hơn 2021.

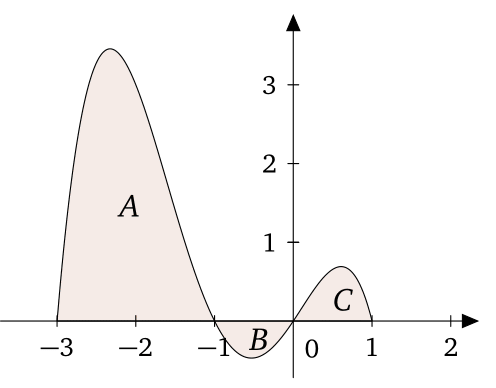
Cho hàm số $y=f\left( x \right)$ liên tục trên đoạn $\left[ -3;1 \right]$ và có đồ thị như hình vẽ dưới. Biết diện tích các hình A,B,C lần lượt là 27, 2 và 3. Tính tích phân $I=\int\limits_{0}^{2}{\left( {{x}^{3}}+x \right)}{f}'\left( {{x}^{2}}-3 \right)\text{d}x$ .

Xét số phức z thỏa mãn $\left| z+3-2i \right|+\left| z-3+i \right|=3\sqrt{5}$ . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức $P=\left| z+2 \right|+\left| z-1-3i \right|$ . Khi đó

Trong không gian với hệ toạ độ Oxyz, cho mặt cầu $\left( S \right):\,{{x}^{2}}\,+\,{{y}^{2}}\,+\,{{z}^{2}}\,=\,3$ . Một mặt phẳng $\left( \alpha \right)$ tiếp xúc với mặt cầu $\left( S \right)$ và cắt các tia $Ox,\,Oy,\,Oz$ lần lượt tại các điểm $A,\,B,\,C$ thoả mãn $O{{A}^{2}}\,+\,O{{B}^{2}}\,+\,O{{C}^{2}}\,=\,27$ . Diện tích của tam giác ABC bằng