
[2021] Trường THPT Trần Phú - Đề thi thử THPT QG năm 2021 môn Toán
Từ khoá: Toán học hàm số tích phân logarit hình học không gian năm 2021 Trường THPT Trần Phú đề thi thử đề thi có đáp án
Đề thi nằm trong bộ sưu tập: 📘 Tuyển Tập Bộ 500 Đề Thi Ôn Luyện Môn Toán THPT Quốc Gia Các Tỉnh Từ Năm 2018-2025 - Có Đáp Án Chi Tiết📘 Tuyển Tập Đề Thi Tham Khảo Các Môn THPT Quốc Gia 2025 🎯
Số câu hỏi: 50 câuSố mã đề: 1 đềThời gian: 1 giờ
194,864 lượt xem 14,978 lượt làm bài
Xem trước nội dung:
Có bao nhiêu cách xếp 6 học sinh ngồi vào một bàn dài có 6 chỗ ?
Cho cấp số nhân (un) với u1 = 3 và u2 = 6. Công bội q của cấp số nhân đã cho bằng
Phương trình có nghiệm là
Thể tích của khối lập phương cạnh 3cm bằng
Tìm tập xác định của hàm số
Tìm họ nguyên hàm của hàm số
Cho khối lăng trụ có diện tích đáy bằng và chiều cao h=a. Thể tích khối lăng trụ đã cho bằng
Tính diện tích xung quanh của hình nón có bán kính đáy r=3 và độ dài đường sinh l=5.
Thể tích khối cầu có bán kính R = 2a bằng
Cho hàm số y = f(x) có bảng biến thiên như sau:
.png)
Hàm số đã cho nghịch biến trên khoảng nào dưới đây ?
Với a là số thực dương tùy ý, bằng
Thể tích của khối trụ có chiều cao bằng h = 10 và bán kính đường tròn đáy bằng r = 4 là
Cho hàm số y = f(x) có bảng biến thiên như sau:
.png)
Giá trị cực đại của hàm số đã cho bằng
Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây.
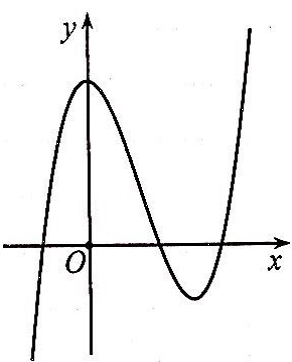
Hàm số đó là hàm số nào?
Tiệm cận đứng của đồ thị hàm số là đường thẳng
Số nghiệm nguyên của bất phương trình là số nào sau đây ?
Cho hàm số có đồ thị như hình bên. Số nghiệm thực của phương trình là
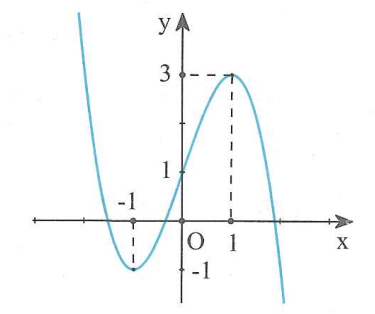
Nếu thì bằng
Số phức liên hợp của số phức z=5-4i là
Cho số phức thỏa mãn . Tính giá trị của biểu thức
Trong mặt phẳng Oxy, cho số phức z=2-3i. Điểm biểu diễn số phức là điểm nào sau đây ?
Trong không gian với hệ tọa độ Oxyz, cho hai điểm Tìm tọa độ trọng tâm G của tam giác OAB.
Trong không gian Oxyz, tính bán kính của mặt cầu
Trong không gian Oxyz, cho mặt phẳng . Vectơ nào sau đây là một vectơ pháp tuyến của (P) ?
Trong không gian Oxyz, đường thẳng đi qua và song song với đường thẳng có phương trình là
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, và . Tính góc giữa đường thẳng SC và mặt phẳng
Cho hàm số có bảng xét dấu của như sau:

Số điểm cực trị của hàm số đã cho là
Gọi M, m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số trên [0;3]. Giá trị của biểu thức M + m bằng
Với a,b là hai số thực dương và khác 1 thỏa mãn . Mệnh đề nào sau đây đúng ?
Số giao điểm của đồ thị hàm số với đường thẳng y=4x+1 là
Tìm tập nghiệm của bất phương trình {{\log }_{2}}\left( 2x-3 \right)<{{\log }_{2}}\left( x-1 \right) .
Cho hình tròn tâm S, bán kính R = 2 . Cắt bỏ đi hình tròn rồi dán lại để tạo ra mặt xung quanh của hình nón như hình vẽ. Tính diện tích xung quanh của hình nón đó.
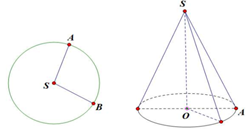
Cho biết với a, b là các số nguyên. Tính K=a+b.
Gọi (H) là hình phẳng giới hạn bởi các đường và x=4. Thể tích của khối tròn xoay được sinh ra khi ta quay (H) quay quanh trục Ox là
Cho hai số phức và . Trên mặt phẳng tọa độ Oxy, điểm biểu diễn số phức có tọa độ là
Gọi là hai nghiệm phức của phương trình , trong đó có phần ảo dương. Tính .
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm và . Viết phương trình mặt phẳng trung trực của đoạn thẳng AB.
Trong không gian với hệ tọa độ Oxyz, phương trình chính tắc của đường thẳng d đi qua điểm và vuông góc với mặt phẳng là
Hội đồng coi thi THPTQG tại huyện X có 30 cán bộ coi thi đến từ 3 trường THPT, trong đó có 12 giáo viên trường A, 10 giáo viên trường B, 8 giáo viên trường C. Chủ tịch hội đồng coi thi gọi ngẫu nhiên 2 cán bộ coi thi lên chứng kiến niêm phong gói đựng bì đề thi. Xác suất để 2 cán bộ coi thi được chọn là giáo viên của 2 trường THPT khác nhau bằng
Cho hình lăng trụ có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của A’ lên (ABC) trùng với tâm O của tam giác ABC, thể tích của khối lăng trụ bằng . Khoảng cách giữa hai đường thẳng và BC bằng
Hỏi có tất cả bao giá trị nguyên của tham số để hàm số nghịch biến trên đoạn ?
Giả sử số lượng một bầy ruồi tại thời điểm t (ngày) so với thời điểm t=0 là là số lượng một bầy ruồi tại thời điểm t=0, k là hằng số tăng trưởng của bầy ruồi. Biết số lượng bầy ruồi tăng lên gấp đôi sau 9 ngày. Hỏi sau bao nhiêu ngày bầy ruồi có 1600 con, biết ?
Cho hàm số có đồ thị như hình bên với Tính giá trị của biểu thức T=a-3b+2c.
Cho một hình trụ tròn xoay và hình vuông ABCD cạnh a có hai đỉnh liên tiếp A,B nằm trên đường tròn đáy thứ nhất của hình trụ, hai đỉnh còn lại nằm trên đường tròn đáy thứ hai của hình trụ như hình vẽ. Mặt phẳng (ABCD) tạo với đáy hình trụ góc . Tính diện tích xung quanh Sxq của hình trụ.
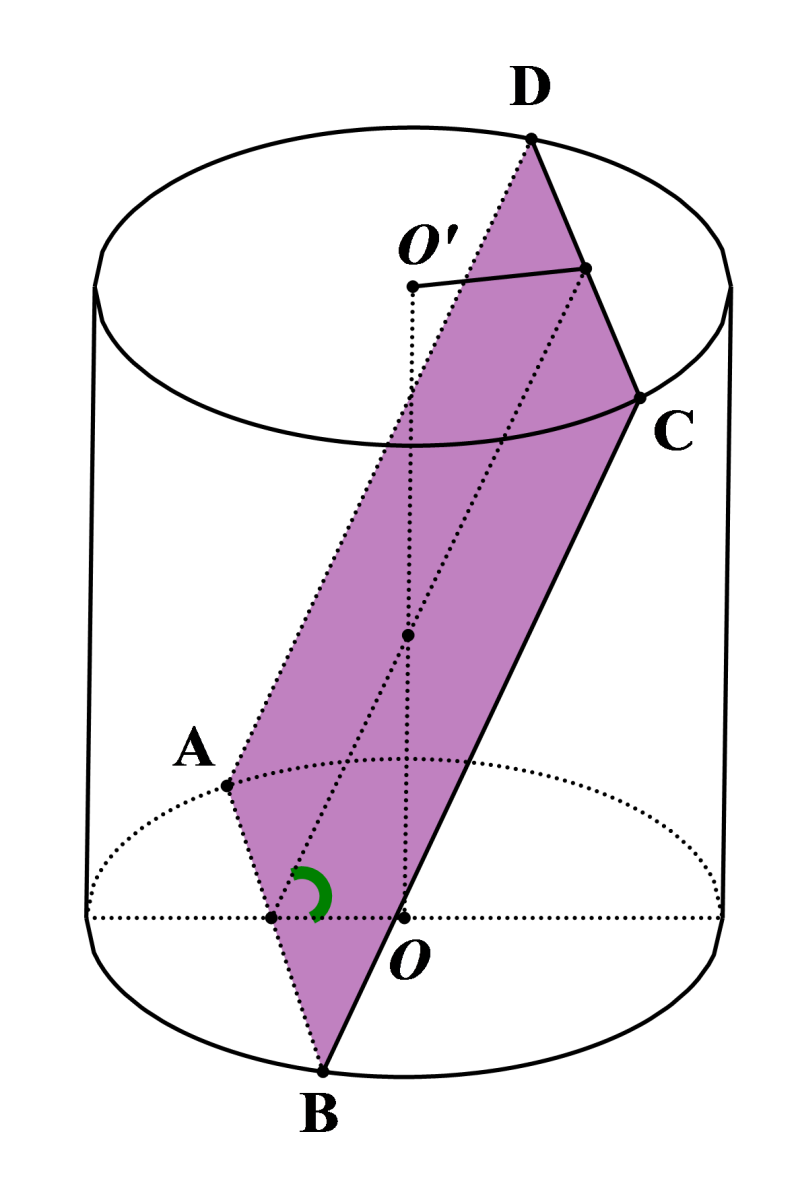
Cho hàm số có đạo hàm liên tục trên Biết và khi đó bằng
Cho hàm số có bảng biến thiên như sau
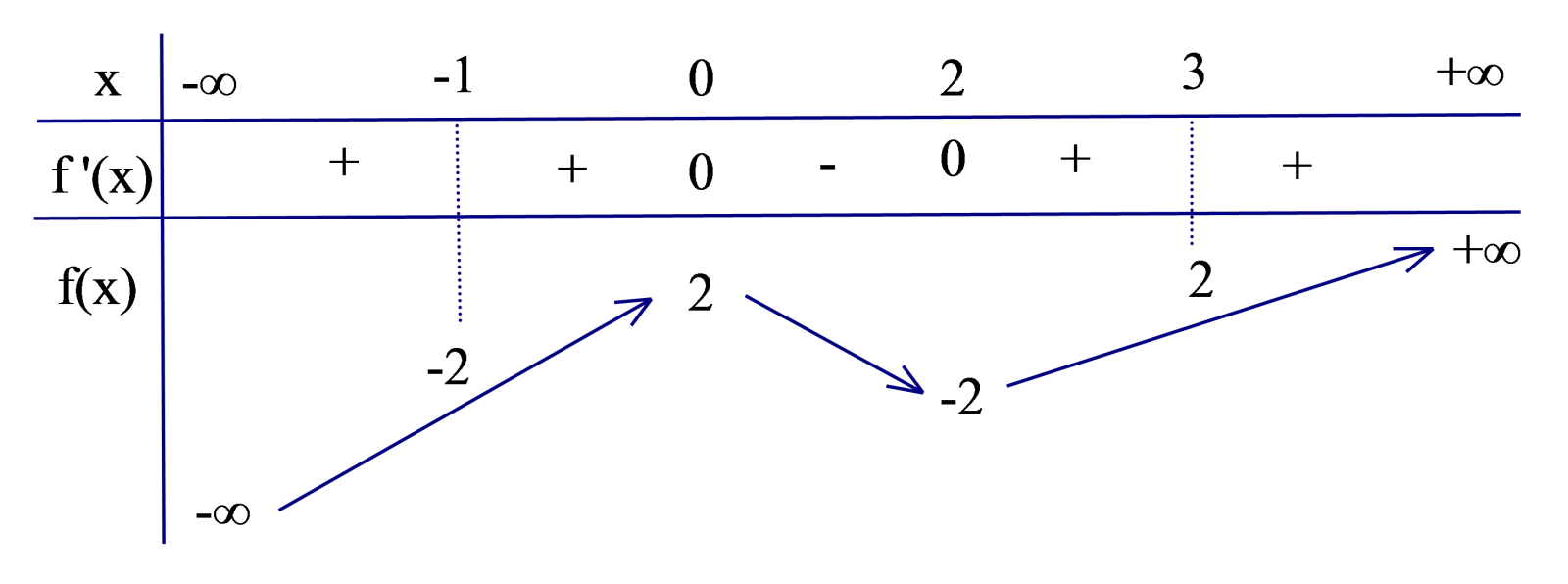
Hỏi có tất cả bao giá trị nguyên của tham số m để phương trình có nghiệm thực ?
Xét các số thực dương x,y,z thay đổi và các số thực a,b,c lớn hơn 1 thỏa mãn . Giá trị nhỏ nhất của thuộc tập nào sau đây ?
Giả sử M,m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn . Hỏi có tất cả bao nhiêu giá trị nguyên của để .
Cho khối lăng trụ đứng ABC.A'B'C' có tất cả các cạnh đều bằng a. Mặt phẳng qua A’B’ và trọng tâm G của tam giác ABC cắt AC, BC lần lượt tại điểm E, F. Tính thể tích V của khối đa diện A'B'ABFE.
Cho hai số dương x,y thỏa với . Hỏi có bao nhiêu số nguyên y thỏa mãn phương trình trên ?
Đề thi tương tự
1 mã đề 40 câu hỏi 1 giờ
192,87314,833
1 mã đề 40 câu hỏi 1 giờ
207,19915,933
1 mã đề 50 câu hỏi 1 giờ
211,42816,260
1 mã đề 50 câu hỏi 1 giờ
204,38815,710
1 mã đề 40 câu hỏi 1 giờ
219,17616,852
1 mã đề 50 câu hỏi 1 giờ
201,85615,518
1 mã đề 50 câu hỏi 1 giờ
192,23914,784
1 mã đề 40 câu hỏi 1 giờ
206,21315,855
1 mã đề 40 câu hỏi 1 giờ
217,71716,736
