[2022] Trường THPT Hoàng Hoa Thám - Đề thi thử THPT QG năm 2022 môn Toán

Cho hai hàm số $y = {\log _a}x,y = {\log _b}x$ (với $a,b$ là hai số thực dương khác $1$ ) có đồ thị lần lượt là $\left( {{C_1}} \right),\left( {{C_2}} \right)$ như hình vẽ. Khẳng định nào sau đây đúng?

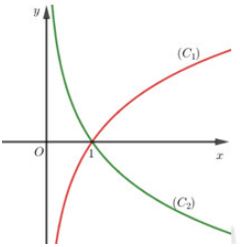
Hình nón có diện tích xung quanh bằng $24\pi$ và bán kính đường tròn đáy bằng $3$ . Đường sinh của hình nón có độ dài bằng:

Tính thể tích $V$ của phần vật thể giới hạn bởi hai mặt phẳng $x = 1$ và $x = 4$ , biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trụ $Ox$ tại điểm có hoành độ $x$$\left( {1 \le x \le 4} \right)$ thì được thiết diện là một hình lục giác đều có độ dài cạnh là $2x$ .

Thể tích khối lăng trụ có diện tích đáy là $B$ và chiều cao $h$ được tính bởi công thức

Cho $F\left( x \right)$ là một nguyên hàm của hàm số $f\left( x \right) = \dfrac{1}{{x - 1}}$ thỏa mãn $F\left( 5 \right) = 2$ và $F\left( 0 \right) = 1$ . Tính $F\left( 2 \right) - F\left( { - 1} \right).$

Cho hàm số $y = f\left( x \right)$ . Đồ thị hàm số $y = f'\left( x \right)$ như hình vẽ. Đặt $g\left( x \right) = 3f\left( x \right) - {x^3} + 3x - m$ , với $m$ là tham số thực. Điều kiện cần và đủ để bất phương trình $g\left( x \right) \ge 0$ nghiệm đúng với $\forall x \in \left[ { - \sqrt 3 ;\sqrt 3 } \right]$ là

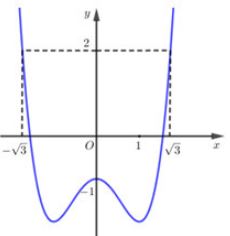
Xét hai số thực $a,b$ dương khác $1$ . Mệnh đề nào sau đây đúng?

Trong không gian $Oxyz$ , cho điểm $A\left( { - 4;0;1} \right)$ và mặt phẳng $\left( P \right)$ : $x - 2y - z + 4 = 0$ . Mặt phẳng $\left( Q \right)$ đi qua điểm $A$ và song song với mặt phẳng $\left( P \right)$ có phương trình là

Trong không gian $Oxyz,$ cho hai mặt phẳng $\left( P \right):x + 2y - 2z - 6 = 0$ và $\left( Q \right):x + 2y - 2z + 3 = 0$ . Khoảng cách giữa hai mặt phẳng $\left( P \right)$ và $\left( Q \right)$ bằng

Có bao nhiêu giá trị nguyên của tham số $m$ để đồ thị của hàm số $y = {x^3} + \left( {m + 2} \right){x^2} + \left( {{m^2} - m - 3} \right)x - {m^2}$ cắt trục hoành tại ba điểm phân biệt?

Cho đồ thị $y = f\left( x \right)$ như hình vẽ sau đây. Biết rằng $\int\limits_{ - 2}^1 {f\left( x \right)dx} = a$ và $\int\limits_1^2 {f\left( x \right)dx = b}$ . Tính diện tích $S$ của phần hình phẳng được tô đậm.

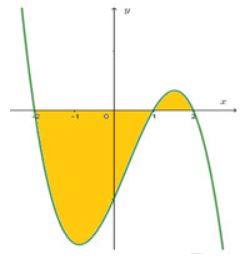
Đường cong trong hình vẽ sau đây là đồ thị của hàm số nào?

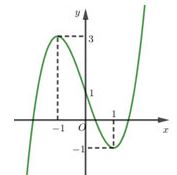
Biết $\int\limits_1^2 {\dfrac{{{x^3}dx}}{{\sqrt {{x^2} + 1} - 1}} = a\sqrt 5 + b\sqrt 2 + c}$ với $a,b,c$ là các số hữu tỉ. Tính $P = a + b + c.$

Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = 2{x^3} - 3{x^2} - 12x + 10$ trên đoạn $\left[ { - 3;3} \right]$ là:

Cho hàm số $y = f\left( x \right)$ có đạo hàm liên tục trên $\mathbb{R}$ và có bảng biến thiên như hình bên dưới. Hàm số đã cho đồng biến trên khoảng nào dưới đây?

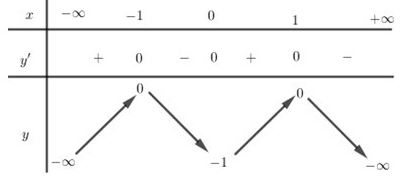
Đồ thị hàm số $y = \dfrac{{\sqrt {x + 7} - 3}}{{{x^2} - 2x}}$ có bao nhiêu đường tiệm cận đứng?

Trong không gian $Oxyz,$ cho mặt phẳng $\left( P \right):2x - y + z + 4 = 0.$ Khi đó mặt phẳng $\left( P \right)$ có một véc tơ pháp tuyến là

Cho $a$ là số thực dương bất kì khác $1$ . Tính $S = {\log _a}\left( {{a^3}\sqrt[4]{a}} \right)$ .

Cho một hình trụ có chiều cao bằng $2$ và bán kính đáy bằng $3$ . Thể tích khối trụ đã cho bằng

Đồ thị hàm số $y = \dfrac{{x + 1}}{{4x - 1}}$ có đường tiệm cận ngang là đường thẳng nào sau đây?

Tập hợp tất cả các giá trị của tham số thực $m$ để hàm số $y = \ln \left( {{x^2} + 1} \right) - mx + 1$ đồng biến trên $\mathbb{R}.$

Trong không gian $Oxyz$ , phương trình của mặt phẳng $\left( P \right)$ đi qua điểm $B\left( {2;1; - 3} \right)$ , đồng thời vuông góc với hai mặt phẳng $\left( Q \right):x + y + 3z = 0,\left( R \right):2x - y + z = 0$ là:

Trong không gian với hệ tọa độ $Oxyz,$ cho mặt phẳng $\left( P \right):x - 2y + 2z - 2 = 0$ và điểm $I\left( { - 1;2; - 1} \right)$ . Viết phương trình mặt cầu $\left( S \right)$ có tâm $I$ và cắt mặt phẳng $\left( P \right)$ theo giao tuyến là đường tròn có bán kính bằng $5.$

Trong không gian với hệ tọa độ $Oxyz$ , cho $\overrightarrow a = \overrightarrow i + 3\overrightarrow j - 2\overrightarrow k$ . Tọa độ của véc tơ $\overrightarrow a$ là

Tìm giá trị cực tiểu ${y_{CT}}$ của hàm số $y = {x^3} - 3{x^2}$

Cho $\int\limits_0^3 {f\left( x \right)dx} = 2$ . Tính giá trị của tích phân $L = \int\limits_0^3 {\left[ {2f\left( x \right) - {x^2}} \right]dx}$ .

Cho cấp số cộng có ${u_1} = - 3;{u_{10}} = 24.$ Tìm công sai $d?$

Cho phương trình ${2^{2x}} - {5.2^x} + 6 = 0$ có hai nghiệm ${x_1},{x_2}$ . Tính $P = {x_1}.{x_2}$ .

Cho hình chóp $S.ABCD$ đều có $AB = 2$ và $SA = 3\sqrt 2 .$ Bán kính của mặt cầu ngoại tiếp hình chóp đã cho bằng

Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh $a$ , cạnh bên $SA$ vuông góc với mặt phẳng đáy và $SA = a\sqrt 6$ . Tính thể tích $V$ của khối chóp $S.ABCD$ .

Cho hình chóp $S.ABC$ có $SA \bot \left( {ABC} \right),$ tam giác $ABC$ vuông ở $B.$$AH$ là đường cao của $\Delta SAB.$ Tìm khẳng định sai.

Từ các chữ số $1;5;6;7$ có thể lập được bao nhiêu số tự nhiên có $4$ chữ số đôi một khác nhau?

Biết bất phương trình ${\log _5}\left( {{5^x} - 1} \right).{\log _{25}}\left( {{5^{x + 1}} - 5} \right) \le 1$ có tập nghiệm là đoạn $\left[ {a;b} \right]$ . Giá trị của $a + b$ bằng

Một người lần đầu gửi vào ngân hàng 100 triệu đồng với kì hạn theo quý (3 tháng), lãi suất $2\%$ một quý. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi quý số tiền lãi sẽ được nhập vào gốc để tính lãi cho quý tiếp theo. Sau đúng 6 tháng, người đó gửi thêm $100$ triệu đồng với kỳ hạn và lãi suất như trước đó. Tổng số tiền người đó nhận được $1$ năm sau khi gửi tiền (cả vốn lẫn lãi) gần nhất với kết quả nào sau đây?

Tiếp tuyến với đồ thị hàm số $y = {x^3} + 3{x^2} - 2$ tại điểm có hoành độ bằng $- 3$ có phương trình là

Cho $\int\limits_1^2 {f\left( x \right)dx = 1}$ và $\int\limits_2^3 {f\left( x \right)dx = - 2.}$ Giá trị của $\int\limits_1^3 {f\left( x \right)dx}$ bằng

Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $B$ , $BC = 2a$ , $SA$ vuông góc với mặt phẳng đáy và $SA = 2a\sqrt 3$ . Gọi $M$ là trung điểm của $AC$ . Khoảng cách giữa hai đường thẳng $AB$ và $SM$ bằng

Trong không gian $Oxyz,$ cho mặt cầu $\left( S \right):{\left( {x - 3} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 1} \right)^2} = 4$ và hai điểm $A\left( { - 1;2; - 3} \right);B\left( {5;2;3} \right)$ . Gọi $M$ là điểm thay đổi trên mặt cầu $\left( S \right)$ . Tính giá trị lớn nhất của biểu thức $2M{A^2} + M{B^2}.$

Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa $24g$ hương liệu, $9$ lít nước và $210g$ đường để pha chế nước cam và nước táo. Để pha chế $1$ lít nước cam cần $30g$ đường, $1$ lít nước và $1g$ hương liệu; còn để pha chế $1$ lít nước táo, cần $10g$ đường, $1$ lít nước và $4g$ hương liệu. Mỗi lít nước cam nhận được $60$ điểm và mỗi lít nước táo nhận được $80$ điểm. Gọi $x,y$ lần lượt là số lít nước cam và nước táo mà mỗi đội cần pha chế sao cho tổng điểm đạt được là lớn nhất. Tính $T = 2{x^2} + {y^2}$ .

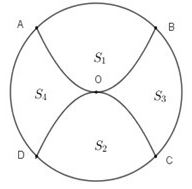
Sân trường có một bồn hoa hình tròn tâm $O.$ Một nhóm học sinh lớp 12 được giao thiết kế bồn hoa, nhóm này định chia bồn hoa thành bốn phần bởi hai đường parabol có cùng đỉnh $O$ và đối xứng nhau qua $O$ (như hình vẽ). Hai đường parabol cắt đường tròn tại bốn điểm $A,B,C,D$ tạo thành một hình vuông có cạnh bằng $4m.$ Phần diện tích ${S_1},{S_2}$ dùng để trồng hoa, phần diện tích ${S_3},{S_4}$ dùng để trồng cỏ. Biết kinh phí trồng hoa là $150.000$ đồng/ $1{m^2},$ kinh phí để trồng cỏ là $100.000$ đồng/ $1{m^2}.$ Hỏi nhà trường cần bao nhiêu tiền để trồng bồn hoa đó? (Số tiền làm tròn đến hàng chục nghìn)

Giả sử hàm số $y = f\left( x \right)$ liên tục, nhận giá trị dương trên $\left( {0; + \infty } \right)$ và thỏa mãn $f\left( 1 \right) = 1$ , $f\left( x \right) = f'\left( x \right)\sqrt {3x + 1}$ , với mọi $x > 0$ . Mệnh đề nào sau đây đúng?

Cho hình $H$ là đa giác đều có $24$ đỉnh. Chọn ngẫu nhiên $4$ đỉnh của $H.$ Tính xác suất sao cho $4$ đỉnh được chọn tạo thành một hình chữ nhật nhưng không phải hình vuông.

Cho lăng trụ đều $ABC.EFH$ có tất cả các cạnh bằng $a$ . Gọi $S$ là điểm đối xứng của $A$ qua $BH$ . Thể tích khối đa diện $ABCSFH$ bằng

Ông $A$ dự định sử dụng hết $5{m^2}$ kính để làm bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có thể tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?

Gọi $S$ là tập hợp các giá trị thực của tham số $m$ sao cho phương trình ${x^9} + 3{x^3} - 9x = m + 3\sqrt[3]{{9x + m}}$ có đúng hai nghiệm thực. Tính tổng các phần tử của $S$ .

Cho $x;y$ là các số thực thỏa mãn ${\log _4}\left( {x + y} \right) + {\log _4}\left( {x - y} \right) \ge 1.$ Tìm giá trị nhỏ nhất của biểu thức $P = 2x - y.$

Cho $k,\,\,n$$\,(k < n)$ là các số nguyên dương. Mệnh đề nào sau đây SAI?

Cho hình lăng trụ $ABC.\,A'B'C'$ có thể tích bằng $V$ . Gọi $M$ là trung điểm cạnh $BB'$ , điểm $N$ thuộc cạnh $CC'$ sao cho $CN = 2C'N$ . Tính thể tích khối chóp $A.\,BCNM$ theo $V$ .

Cho hàm số $y = {x^3} - 3x + 1$ . Mệnh đề nào sau đây đúng?

Cho tứ diện $ABCD$ , gọi ${G_1},\,{G_2}$ lần lượt là trọng tâm các tam giác $BCD$ và $ACD$ . Mệnh đề nào sau đây SAI?