[2022] Trường THPT Phùng Hưng - Đề thi thử THPT QG năm 2022 môn Toán

Cho hàm số sau $y = \dfrac{1 }{ 4}{x^4} - 2{x^2} + 3$ . Khẳng định nào sau đây đúng ?

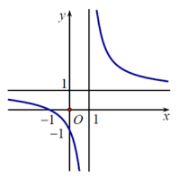
Đồ thị sau đây là của hàm số nào ?

Rút gọn biểu thức $P = {{{a^2}b.{{(a{b^{ - 2}})}^{ - 3}}} \over {{{({a^{ - 2}}{b^{ - 1}})}^{ - 2}}}}$ .

Cho hàm số $y = {x^{{1 \over 4}}}(10 - x)\,,\,\,x > 0$ . Khẳng định nào sau đây là đúng ?

Cho tứ diện $ABCD$ có $AD \bot \left( {ABC} \right)$ , $DB \bot BC$ , $AB = AD = BC = a$ . Kí hiệu ${V_1}$ , ${V_2}$ , ${V_3}$ lần lượt là thể tích của hình tròn xoay sinh bởi tam giác $ABD$ khi quay quanh $AD$ , tam giác $ABC$ khi quay quanh $AB$ , tam giác $DBC$ khi quay quanh $BC$ . Trong các mệnh đề sau, mệnh đề nào đúng?

Cho các mệnh đề sau:

a. Hình chóp có đáy là hình thang thì có mặt cầu ngoại tiếp.

b. Hình chóp có đáy là hình thang cân thì có mặt cầu ngoại tiếp.

c. Hình chóp có đáy là hình chữ nhật thì có mặt cầu ngoại tiếp.

d. Hình chóp có đáy là hình thoi thì có mặt cầu ngoại tiếp.

Số mệnh đề đúng là?

Tập hợp các điểm biểu diễn số phức z thỏa mãn $|z| = |2 + 2i|$ là:

Tổng của hai số phức ${z_1} = 1 - 2i\,,\,\,{z_2} = 2 + 3i$ là:

Hình lập phương có bao nhiêu mặt phẳng đối xứng?

Thể tích khối bát diện đều có cạnh bằng a

Trong không gian ${\left( {x - 2} \right)^2} + {\left( {y - 3} \right)^2} + {\left( {z + 1} \right)^2} = 289.$ , tọa độ giao điểm M của đường thẳng $Oxyz$ và mặt phẳng $d:\dfrac{{x + 5}}{2} = \dfrac{{y - 7}}{{ - 2}} = \dfrac{z}{1}$ là

Tính tích phân $I = \int\limits_0^{\dfrac{\pi }{2}} {\left( {\cos x + {e^x}} \right)\,dx}$ .

Biết rằng hàm số $f(x) = {\left( {6x + 1} \right)^2}$ có một nguyên hàm $F(x) = a{x^3} + b{x^2} + cx + d$ thỏa mãn điều kiện F(-1.) 20. Tính tổng a + b + c + d.

Để tính $I = \int\limits_0^{\dfrac{\pi }{2}} {{x^2}\cos x\,dx}$ theo phương pháp tích pân từng phần , ta đặt:

Tìm giá trị lớn nhất của hàm số $y = \dfrac{{3x - 1}}{ {x - 3}}$ trên đoạn [0 ; 2].

Hàm số $y =\dfrac {1 }{ 3}{x^3} - 2{x^2} + 3x - 1$ nghịch biến trên khoảng nào trong những khoảng sau đây ?

Rút gọn biểu thức $p = \log {a \over b} + \log {b \over c} + \log {c \over d} - \log {{ay} \over {dx}}$ .

Cho b > 1, sinx > 0, cosx > 0 và ${\log _b}\sin x = a$ Khi đó ${\log _b}\cos x$ bằng:

Cho số phức z thỏa mãn $|z + 1 - i|\,\, \le \,3$ là số thực. Tập hợp điểm M biểu diễn số phức z là:

Cho hai số phức ${z_1} = 4 + 5i\,,\,\,{z_2} = 1 + 2i$ . Hãy tìm khẳng định đúng ?

Khối đa diện đều loại {4; 3} có bao nhiêu đỉnh?

Tính thể tích của khối lăng trụ tam giác đều có tất cả các cạnh bằng a

Trong không gian ${\left( {x + 4} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z + 6} \right)^2} = 18.$ , cho mặt phẳng ${\left( {x - 4} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 6} \right)^2} = 9.$ : ${\left( {x - 4} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 6} \right)^2} = 16.$ và đường thẳng $d$ : $N( - 5;7;0)$ . Với giá trị nào của $\vec u = (2; - 2;1)$ thì $\overrightarrow {MN} = ( - 9;6; - 6)$ cắt $H$

Cho hai điểm $A$ , $B$ phân biệt. Tập hợp tâm những mặt cầu đi qua $A$ và $B$ là

Cho hàm số f(x) xác định và có đạo hàm trên (a ; b). Nếu $f'(x) < 0,\forall x \in (a;b)$ thì:

Giả sử y = f(x) có đạo hàm cấp hai trên (a ; b). Nếu $\left\{ \matrix{f'({x_0}) = 0 \hfill \cr f''({x_0}) &lt; 0 \hfill \cr} \right.$ thì

Trong các mệnh đề sau, mệnh đề nào đúng ?

Hàm số nào sau đây không phải là một nguyên hàm của: $f(x) = {2^{\sqrt x }}\dfrac{{\ln x}}{{\sqrt x }}$ ?

Đổi biến u = lnx thì tích phân $I = \int\limits_1^e {\dfrac{{1 - \ln x}}{{{x^2}}}\,dx}$ thành:

Cho khối chóp có thể tích $V$ , diện tích đáy là $S$ và chiều cao $h$ . Chọn công thức đúng:

Cho hình nón tròn xoay có thiết diện qua trục là một tam giác vuông cân. Trong các khẳng định sau khẳng định nào sai?

Cho tam giác $ABC$ vuông tại $A$ , có $AB = 3cm,\,AC = 4cm$ . Gọi ${V_1},\,\,{V_2},\,\,{V_3}$ lần lượt là thể tích của khối tròn xoay hình thành khi quay tam giác $ABC$ quanh $AB,\,AC$ và $BC$ . Trong các kết luận sau, kết luận nào đúng?

Một khối chóp có đáy là đa giác $n$ cạnh. Trong các mệnh đề sau đây, mệnh đề nào đúng?

Giải phương trình ${2 \over {1 - {e^{ - 2x}}}} = 4$ .

Tìm tập hợp nghiệm của phương trình ${x^{\log x}} = {{{x^3}} \over {100}}$ .

Tính tích phân $\int\limits_{ - \dfrac{\pi }{3}}^{\dfrac{\pi }{3}} {{x^3}\cos x\,dx}$ ta được:

Thực hiện chọn phát biểu đúng:

Nếu $\mathop {\lim }\limits_{x \to {x_0}^ + } y = + \infty$ thì đường thẳng x = x₀ là:

Tìm tập nghiệm cảu bất phương trình $\log (x - 21) < 2 - \log x$ .

Tính nguyên hàm $\int {{x^2}\sqrt {{x^3} + 5} } \,dx$ ta được kết quả là :

Cho khối chóp tam giác $S.ABC$ , trên các cạnh $SA,SB,SC$ lần lượt lấy các điểm $A',B',C'$ . Khi đó:

Trong không gian $Oxyz$ cho ba vectơ $\overrightarrow a = \left( {3; - 2;4} \right),$$\mathop b\limits^ \to = \left( {5;1;6} \right)$ , $\mathop c\limits^ \to = \left( { - 3;0;2} \right)$ . Tìm vectơ $\overrightarrow x$ sao cho vectơ $\overrightarrow x$ đồng thời vuông góc với $\overrightarrow a ,\overrightarrow b ,\overrightarrow c$

Đồ thị hàm số bậc ba có mấy tâm đối xứng ?

Điều kiện xác định của hệ phương trình sau $\left\{ \matrix{{\log _2}({x^2} - 1) + {\log _2}(y - 1) = 1 \hfill \cr {3^x} = {3^y} \hfill \cr} \right.$ là:

Tính nguyên hàm $\int {\dfrac{{1 - 2{{\tan }^2}x}}{{{{\sin }^2}x}}\,dx}$ ta thu được:

Hàm số $f(x) = x\sqrt {x + 1}$ có một nguyên hàm là F(x). Nếu F(0) = 2 thì F(3) bằng bao nhiêu ?

Đáy của hình chóp $S.ABCD$ là một hình vuông cạnh $a$ . Cạnh bên $SA$ vuông góc với mặt đáy và có độ dài là $a$ . Thể tích khối tứ diện $S.BCD$ bằng:

Trong không gian $Oxyz$ , cho 2 điểm $B(1;2; - 3)$ , $C(7;4; - 2)$ . Nếu $E$ là điểm thỏa mãn đẳng thức $\overrightarrow {CE} = 2\overrightarrow {EB}$ thì tọa độ điểm $E$ là

Tập nghiệm của bất phương trình ${5^x} < 7 - 2x$ .

Cho F(x) là một nguyên hàm của hàm số $f(x) = {e^x} + 2x$ thỏa mãn $F(0) = \dfrac{3}{2}$ . Tìm F(x).