Trang chủ Đề thi [2022] Trường THPT Tân Phong - Đề thi thử THPT QG năm 2022 môn Toán
thumbnail

[2022] Trường THPT Tân Phong - Đề thi thử THPT QG năm 2022 môn Toán

Thời gian làm bài: 1 giờ

Đề thi nằm trong bộ sưu tập: 📘 Tuyển Tập Bộ 500 Đề Thi Ôn Luyện Môn Toán THPT Quốc Gia Các Tỉnh Từ Năm 2018-2025 - Có Đáp Án Chi Tiết


Bạn chưa làm đề thi này!!!

Hãy bắt đầu chinh phục nào!



 

Xem trước nội dung:

Câu 1: 1 điểm

Có bao nhiêu số nguyên dương m để bất phương trình m.9x−(2m+1).6x+m.4x≤0m{{.9}^{x}}-\left( 2m+1 \right){{.6}^{x}}+m{{.4}^{x}}\le 0 nghiệm đúng với mọi x∈(0;1)?x\in \left( 0;1 \right)?

A.  
7
B.  
4
C.  
5
D.  
6
Câu 2: 1 điểm

Biết F(x)F\left( x \right) là một nguyên hàm của hàm số f(x)=e2xf\left( x \right)={{e}^{2x}} và F(0)=32.F\left( 0 \right)=\frac{3}{2}. Tính F(12).F\left( \frac{1}{2} \right).

A.  
F(12)=12e+2F\left( \frac{1}{2} \right)=\frac{1}{2}e+2
B.  
F(12)=2e+1F\left( \frac{1}{2} \right)=2e+1
C.  
F(x)=12e+12F\left( x \right)=\frac{1}{2}e+\frac{1}{2}
D.  
F(12)=12e+1F\left( \frac{1}{2} \right)=\frac{1}{2}e+1
Câu 3: 1 điểm

Trên giá sách có 4 quyển sách toán, 3 quyển sách lý, 2 quyển sách hóa. Lấy ngẫu nhiên 3 quyển sách. Tính xác suất P để 3 quyển được lấy ra có ít nhất một quyển sách là toán.

A.  
P=27P=\frac{2}{7}
B.  
P=542P=\frac{5}{42}
C.  
P=3742P=\frac{37}{42}
D.  
P=121P=\frac{1}{21}
Câu 4: 1 điểm

Cho tam giác ABC có ABC^=450,ACB^=300,AB=22.\widehat{ABC}={{45}^{0}},\widehat{ACB}={{30}^{0}},AB=\frac{\sqrt{2}}{2}. Quay tam giác ABC xung quanh cạnh BC ta được khối tròn xoay có thể tích V bằng:

A.  
V=π(1+3)8V=\frac{\pi \left( 1+\sqrt{3} \right)}{8}
B.  
V=π3(1+3)2V=\frac{\pi \sqrt{3}\left( 1+\sqrt{3} \right)}{2}
C.  
V=π(1+3)3V=\frac{\pi \left( 1+\sqrt{3} \right)}{3}
D.  
V=π(1+3)24V=\frac{\pi \left( 1+\sqrt{3} \right)}{24}
Câu 5: 1 điểm

Cho hàm số y=2x+11−xy=\frac{2x+1}{1-x} . Mệnh đề nào sau đây là đúng?

A.  
Hàm số đồng biến trên R\{1}R\backslash \left\{ 1 \right\} .
B.  
Hàm số đồng biến trên (−∞;1)\left( -\infty ;1 \right) và (1;+∞).\left( 1;+\infty \right).
C.  
Hàm số nghịch biến trên (−∞;1)\left( -\infty ;1 \right) và (1;+∞).\left( 1;+\infty \right).
D.  
Hàm số đồng biến trên (−∞;1)∪(1;+∞).\left( -\infty ;1 \right)\cup \left( 1;+\infty \right).
Câu 6: 1 điểm

Tìm tập xác định của hàm số y=(3x2−1)13.y={{\left( 3{{x}^{2}}-1 \right)}^{\frac{1}{3}}}.

A.  
D=RD=R
B.  
D=R\{±13}D=R\backslash \left\{ \pm \frac{1}{\sqrt{3}} \right\}
C.  
D=(−∞;−13]∪[13;+∞)D=\left( -\infty ;-\frac{1}{\sqrt{3}} \right]\cup \left[ \frac{1}{\sqrt{3}};+\infty \right)
D.  
D=(−∞;−13)∪(13;+∞)D=\left( -\infty ;-\frac{1}{\sqrt{3}} \right)\cup \left( \frac{1}{\sqrt{3}};+\infty \right)
Câu 7: 1 điểm

Cho hàm số y=f(x)y=f\left( x \right) liên tục trên R và thỏa mãn ∫f(x)dx=4x3−3x2+2x+C\int\limits_{{}}^{{}}{f\left( x \right)dx}=4{{x}^{3}}-3{{x}^{2}}+2x+C . Hàm số f(x)f\left( x \right) là hàm số nào trong các hàm số sau?

Câu 8: 1 điểm

Cho hàm số y=2x+1x+1y=\frac{2x+1}{x+1} có đồ thị (C)\left( C \right) . Tìm tất cả các giá trị thực của tham số m sao cho đường thẳng d:  y=x+m−1d:\,\,y=x+m-1 cắt (C)\left( C \right) tại hai điểm phân biệt ABAB thỏa mãn AB=23AB=2\sqrt{3} .

A.  
m=4±3m=4\pm \sqrt{3}
B.  
m=2±3m=2\pm \sqrt{3}
C.  
m=2±10m=2\pm \sqrt{10}
D.  
m=4±10m=4\pm \sqrt{10}
Câu 9: 1 điểm

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P):  2x−5z+1=0\left( P \right):\,\,2x-5z+1=0 , vectơ n→\overrightarrow{n} nào sau đây là vectơ pháp tuyến của (P)?

A.  
n→=(2;0;−5)\overrightarrow{n}=\left( 2;0;-5 \right)
B.  
n→=(2;0;5)\overrightarrow{n}=\left( 2;0;5 \right)
C.  
n→=(2;−5;1)\overrightarrow{n}=\left( 2;-5;1 \right)
D.  
n→=(0;2;−5)\overrightarrow{n}=\left( 0;2;-5 \right)
Câu 10: 1 điểm

Trong không gian với hệ tọa độ Oxyz, cho M(3;2;1)M\left( 3;2;1 \right) . Mặt phẳng (P) đi qua M và cắt các trục tọa độ Ox, Oy, Oz tại A, B, C sao cho M là trục tâm tam giác ABC. Phương trình mặt phẳng (P) là:

A.  
x+y+z−6=0x+y+z-6=0
B.  
x3+y2+z1=0\frac{x}{3}+\frac{y}{2}+\frac{z}{1}=0
C.  
3x+2y+z−14=03x+2y+z-14=0
D.  
x3+y2+z1=1\frac{x}{3}+\frac{y}{2}+\frac{z}{1}=1
Câu 11: 1 điểm

Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;0;0),B(0;2;0),C(0;0;3).A\left( 1;0;0 \right),B\left( 0;2;0 \right),C\left( 0;0;3 \right). Gọi M là điểm thay đổi trên mặt phẳng (ABC) và N là điểm trên tia OM sao cho OM.ON = 1. Biết rằng N luôn thuộc mặt cầu cố định. Viết phương trình mặt cầu đó?

A.  
(x−3649)2+(y−1849)2+(z−1249)2=2549{{\left( x-\frac{36}{49} \right)}^{2}}+{{\left( y-\frac{18}{49} \right)}^{2}}+{{\left( z-\frac{12}{49} \right)}^{2}}=\frac{25}{49}
B.  
(x−12)2+(y−14)2+(z−16)2=49144{{\left( x-\frac{1}{2} \right)}^{2}}+{{\left( y-\frac{1}{4} \right)}^{2}}+{{\left( z-\frac{1}{6} \right)}^{2}}=\frac{49}{144}
C.  
x2+(y+1)2+(z−2)2=4{{x}^{2}}+{{\left( y+1 \right)}^{2}}+{{\left( z-2 \right)}^{2}}=4
D.  
x2+(y−1)2+(z−2)2=4{{x}^{2}}+{{\left( y-1 \right)}^{2}}+{{\left( z-2 \right)}^{2}}=4
Câu 12: 1 điểm

Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác vuông tại B, AB=a,BC=a3AB=a,BC=a\sqrt{3} , góc hợp bởi đường thẳng AA’ và mặt phẳng (A’B’C) bằng 450{{45}^{0}} , hình chiếu vuông góc của B’ lên (ABC) trùng với trọng tâm của tam giác ABC. Tính thế tích V khối lăng trụ ABC.A’B’C’.

A.  
V=3a39V=\frac{\sqrt{3}{{a}^{3}}}{9}
B.  
V=3a33V=\frac{\sqrt{3}{{a}^{3}}}{3}
C.  
V=a3V={{a}^{3}}
D.  
V=a33V=\frac{{{a}^{3}}}{3}
Câu 13: 1 điểm

Cho log⁡9x=log⁡12y=log⁡16(x+y){{\log }_{9}}x={{\log }_{12}}y={{\log }_{16}}\left( x+y \right) . Tính giá trị tỷ số xy\frac{x}{y} ?

A.  
xy=3−52\frac{x}{y}=\frac{3-\sqrt{5}}{2}
B.  
xy=−1−52\frac{x}{y}=\frac{-1-\sqrt{5}}{2}
C.  
xy=−1+52\frac{x}{y}=\frac{-1+\sqrt{5}}{2}
D.  
xy=3+52\frac{x}{y}=\frac{3+\sqrt{5}}{2}
Câu 14: 1 điểm

Từ các chữ số 0, 1, 2, 3, 4 có thể lập được bao nhiêu số có năm chữ số khác nhau từng đôi một?

A.  
3125
B.  
120
C.  
96
D.  
2500
Câu 15: 1 điểm

Tính diện tích S của hình phẳng giới hạn bởi đường thẳng y=2x+1y=2x+1 và đồ thị hàm số y=x2−x+3y={{x}^{2}}-x+3

A.  
S=17S=\frac{1}{7}
B.  
S=18S=\frac{1}{8}
C.  
S=16S=\frac{1}{6}
D.  
S=−16S=-\frac{1}{6}
Câu 16: 1 điểm

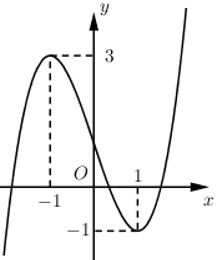
Đường cong trong hình bên là đồ thị của hàm số nào dưới đây?

A.  
y=−x3+3x−1y=-{{x}^{3}}+3x-1
B.  
y=2x3−3x2+1y=2{{x}^{3}}-3{{x}^{2}}+1
C.  
y=x3−3x+1y={{x}^{3}}-3x+1
D.  
y=2x3−6x+1y=2{{x}^{3}}-6x+1
Câu 17: 1 điểm

Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số y=(m+1)x3+(m+1)x2−2x+2y=\left( m+1 \right){{x}^{3}}+\left( m+1 \right){{x}^{2}}-2x+2 nghịch biến trên R.

A.  
6
B.  
8
C.  
7
D.  
5
Câu 18: 1 điểm

Cho biết 0<a<10<a<1 . Chọn khẳng định đúng trong các khẳng định sau:

A.  
Nếu 0<x1<x20<{{x}_{1}}<{{x}_{2}} thì log⁡ax1<log⁡ax2{{\log }_{a}}{{x}_{1}}<{{\log }_{a}}{{x}_{2}}
B.  
log⁡ax<1{{\log }_{a}}x<1 thì 0<x><a0<x><a > >
C.  
log⁡ax>0{{\log }_{a}}x>0 khi x>1x>1
D.  
Đồ thị hàm số y=log⁡axy={{\log }_{a}}x nhận trục Oy làm tiệm cận đứng
Câu 19: 1 điểm

Xác định phần ảo của số phức z=12−18iz=12-18i ?

A.  
−18-18
B.  
−18i-18i
C.  
1212
D.  
1818
Câu 20: 1 điểm

Cho hàm số f(x)f\left( x \right) có đạo hàm f′(x)=x2(x−1)3(x−2)f'\left( x \right)={{x}^{2}}{{\left( x-1 \right)}^{3}}\left( x-2 \right) . Số điểm cực trị của hàm số f(x)f\left( x \right) bằng:

A.  
3
B.  
2
C.  
0
D.  
1
Câu 21: 1 điểm

Cho số phức zz thỏa mãn (3+i)∣z∣=−2+14iz+1−3i\left( 3+i \right)\left| z \right|=\frac{-2+14i}{z}+1-3i . Chọn khẳng định đúng?

A.  
134<∣z∣<5\frac{13}{4}<\left| z \right|<5
B.  
1<∣z∣<321<\left| z \right|<\frac{3}{2}
C.  
32<∣z∣<2\frac{3}{2}<\left| z \right|<2
D.  
74<∣z∣<115\frac{7}{4}<\left| z \right|<\frac{11}{5}
Câu 22: 1 điểm

Tìm tập nghiệm S của bất phương trình log⁡2(3x−2)>log⁡2(6−5x){{\log }_{2}}\left( 3x-2 \right)>{{\log }_{2}}\left( 6-5x \right) .

A.  
S=(1;65)S=\left( 1;\frac{6}{5} \right)
B.  
S=(23;65)S=\left( \frac{2}{3};\frac{6}{5} \right)
C.  
S=(1;+∞)S=\left( 1;+\infty \right)
D.  
S=(23;1)S=\left( \frac{2}{3};1 \right)
Câu 23: 1 điểm

Cho chuyển động thẳng xác định bởi mặt phương trình s=12(t4+3t2),s=\frac{1}{2}\left( {{t}^{4}}+3{{t}^{2}} \right), t được tính bằng giây, s được tính bằng m. Vận tốc của chuyển động tại t = 4 (giây) bằng:

A.  
0 m/s0\,m/s
B.  
200 m/s200\,m/s
C.  
150 m/s150\,m/s
D.  
140 m/s140\,m/s
Câu 24: 1 điểm

Trong không gian với hệ tọa độ Oxyz cho ba mặt phẳng (P):  x−2y+z−1=0\left( P \right):\,\,x-2y+z-1=0 , (Q):  x−2y+z+8=0\left( Q \right):\,\,x-2y+z+8=0 và (R):  x−2y+z−4=0\left( R \right):\,\,x-2y+z-4=0 . Một đường thẳng d thay đổi cắt ba mặt phẳng (P);(Q);(R)\left( P \right);\left( Q \right);\left( R \right) lần lượt tại A, B, C. Đặt T=AB24+144ACT=\frac{A{{B}^{2}}}{4}+\frac{144}{AC} . Tìm giá trị nhỏ nhất của TT .

A.  
min⁡T=108\min T=108
B.  
min⁡T=5423\min T=54\sqrt[3]{2}
C.  
min⁡T=96\min T=96
D.  
min⁡T=7223\min T=72\sqrt[3]{2}
Câu 25: 1 điểm

Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(−1;2;−4)A\left( -1;2;-4 \right) và B(1;0;2)B\left( 1;0;2 \right) . Viết phương trình đường thẳng d đi qua hai điểm A và B.

A.  
d:  x+11=y−21=z+43d:\,\,\frac{x+1}{1}=\frac{y-2}{1}=\frac{z+4}{3}
B.  
d:  x−11=y+21=z−43d:\,\,\frac{x-1}{1}=\frac{y+2}{1}=\frac{z-4}{3}
C.  
d:  x+11=y−2−1=z+43d:\,\,\frac{x+1}{1}=\frac{y-2}{-1}=\frac{z+4}{3}
D.  
d:  x−11=y+2−1=z−43d:\,\,\frac{x-1}{1}=\frac{y+2}{-1}=\frac{z-4}{3}
Câu 26: 1 điểm

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA = 3a và SA vuông góc với mặt phẳng đáy. Tính thể tích V của khối chóp S.ABCD.

A.  
V=a33V=\frac{{{a}^{3}}}{3}
B.  
V=9a3V=9{{a}^{3}}
C.  
V=a3V={{a}^{3}}
D.  
V=3a3V=3{{a}^{3}}
Câu 27: 1 điểm

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu có phương trình x2+y2+z2−2x+4y−6z+9=0{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-2x+4y-6z+9=0 . Tìm tâm I và bán kính R của mặt cầu?

A.  
I(1;−2;3)I\left( 1;-2;3 \right) và R=5R=\sqrt{5}
B.  
I(−1;2;−3)I\left( -1;2;-3 \right) và R=5R=\sqrt{5}
C.  
I(1;−2;3)I\left( 1;-2;3 \right) và R=5R=5
D.  
I(−1;2;−3)I\left( -1;2;-3 \right) và R=5R=5
Câu 28: 1 điểm

Cho khai triển nhị thức Newton (2−3x)2x{{\left( 2-3x \right)}^{2x}} , biết rằng n là số nguyên dương thỏa mãn C2n+11+C2n+13+C2n+15+...+C2n+12n+1=1024C_{2n+1}^{1}+C_{2n+1}^{3}+C_{2n+1}^{5}+...+C_{2n+1}^{2n+1}=1024 . Tìm hệ số của x7{{x}^{7}} trong khai triển (2−3x)2n{{\left( 2-3x \right)}^{2n}}

A.  
−2099520-2099520
B.  
−414720-414720
C.  
414720414720
D.  
20995202099520
Câu 29: 1 điểm

Tính đạo hàm của hàm số y=log⁡2018(3x+1)y={{\log }_{2018}}\left( 3x+1 \right) .

A.  
y′=13x+1y'=\frac{1}{3x+1}
B.  
y′=1(3x+1)ln⁡2018y'=\frac{1}{\left( 3x+1 \right)\ln 2018}
C.  
y′=33x+1y'=\frac{3}{3x+1}
D.  
y′=3(3x+1)ln⁡2018y'=\frac{3}{\left( 3x+1 \right)\ln 2018}
Câu 30: 1 điểm

Cho hàm số f(x)f\left( x \right) có đạo hàm f′(x)f'\left( x \right) liên tục trên [a;b];f(b)=5\left[ a;b \right];f\left( b \right)=5 và ∫abf′(x)dx=35\int\limits_{a}^{b}{f'\left( x \right)dx}=3\sqrt{5} . Tính giá trị f(a)?f\left( a \right)?

A.  
f(a)=3(5−3)f\left( a \right)=\sqrt{3}\left( \sqrt{5}-3 \right)
B.  
f(a)=5(5−3)f\left( a \right)=\sqrt{5}\left( \sqrt{5}-3 \right)
C.  
f(a)=35f\left( a \right)=3\sqrt{5}
D.  
f(a)=5(3−5)f\left( a \right)=\sqrt{5}\left( 3-\sqrt{5} \right)
Câu 31: 1 điểm

Tìm tất cả các giá trị y0{{y}_{0}} để đường thẳng y=y0y={{y}_{0}} cắt đồ thị hàm số y=x4−x2y={{x}^{4}}-{{x}^{2}} tại bốn điểm phân biệt?

A.  
−14<y0<0-\frac{1}{4}<{{y}_{0}}<0
B.  
y0>14{{y}_{0}}>\frac{1}{4}
C.  
y0<−14{{y}_{0}}<-\frac{1}{4}
D.  
0<y0<140<{{y}_{0}}<\frac{1}{4}
Câu 32: 1 điểm

Cho hình lăng trụ ABC.A’B’C’ có mặt đáy ABC là tam giác đều cạnh AB = 2a. Hình chiếu vuông góc của A’ trên (ABC) trùng với trung điểm H của cạnh AB. Biết góc giữa cạnh bên và mặt đáy bằng 600{{60}^{0}} . Tính tang của góc φ\varphi giữa hai mặt phẳng (ABC) và (BCC’B’).

A.  
tan⁡φ=2\tan \varphi =2
B.  
tan⁡φ=4\tan \varphi =4
C.  
tan⁡φ=14\tan \varphi =\frac{1}{4}
D.  
tan⁡φ=2\tan \varphi =\sqrt{2}
Câu 33: 1 điểm

Cho hàm số y=14x4−2x2+2018y=\frac{1}{4}{{x}^{4}}-2{{x}^{2}}+2018 . Khẳng định nào sau đây là đúng?

A.  
Hàm số có một điểm cực tiểu và không có điểm cực đại.
B.  
Hàm số có một điểm cực đại và không có điểm cực tiểu.
C.  
Hàm số có một điểm cực tiểu và hai điểm cực đại.
D.  
Hàm số có một điểm cực đại và hai điểm cực tiểu.
Câu 34: 1 điểm

Trong không gian với hệ tọa độ Oxyz, cho hai vectơ a→=(3;−2;1),b→=(−2;−1;1)\overrightarrow{a}=\left( 3;-2;1 \right),\overrightarrow{b}=\left( -2;-1;1 \right) . Tính P=a→.b→P=\overrightarrow{a}.\overrightarrow{b} ?

A.  
P=−12P=-12
B.  
P=−3P=-3
C.  
P=12P=12
D.  
P=3P=3
Câu 35: 1 điểm

Phương trình sin⁡2x+cos⁡x=0\sin 2x+\cos x=0 có tổng các nghiệm trong khoảng (0;2π)\left( 0;2\pi \right) bằng:

A.  
6π6\pi
B.  
2π2\pi
C.  
3π3\pi
D.  
5π5\pi
Câu 36: 1 điểm

Cho hai số phức z=2+3i,z′=3−2iz=2+3i,z'=3-2i . Tìm môđun của số phức w=z.z′w=z.z' .

A.  
∣w∣=13\left| w \right|=\sqrt{13}
B.  
∣w∣=13\left| w \right|=13
C.  
∣w∣=12\left| w \right|=12
D.  
∣w∣=14\left| w \right|=14
Câu 37: 1 điểm

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B và cạnh bên SB vuông góc với mặt phẳng đáy. Cho biết SB = 3a, AB = 4a, BC = 2a. Tính khoảng cách d từ điểm B đến mặt phẳng (SAC).

A.  
d=45ad=\frac{4}{5}a
B.  
d=31414ad=\frac{3\sqrt{14}}{14}a
C.  
d=126161ad=\frac{12\sqrt{61}}{61}a
D.  
d=122929ad=\frac{12\sqrt{29}}{29}a
Câu 38: 1 điểm

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = 2a. Các cạnh bên của hình chóp đều bằng a2a\sqrt{2} . Tính góc giữa hai đường thẳng AB và SC.

A.  
300{{30}^{0}}
B.  
600{{60}^{0}}
C.  
900{{90}^{0}}
D.  
450{{45}^{0}}
Câu 39: 1 điểm

Cho hình nón có bán kính đáy bằng a, thể tích khối nón tương ứng V=2πa3.V=2\pi {{a}^{3}}. Diện tích xung quanh của hình nón là:

A.  
Sxq=37πa{{S}_{xq}}=\sqrt{37}\pi a
B.  
Sxq=37πa2{{S}_{xq}}=\sqrt{37}\pi {{a}^{2}}
C.  
Sxq=237πa2{{S}_{xq}}=2\sqrt{37}\pi {{a}^{2}}
D.  
Sxq=5πa2{{S}_{xq}}=\sqrt{5}\pi {{a}^{2}}
Câu 40: 1 điểm

Biết rằng I=∫01xcos⁡2xdx=14(asin⁡2+bcos⁡2+c)I=\int\limits_{0}^{1}{x\cos 2xdx}=\frac{1}{4}\left( a\sin 2+b\cos 2+c \right) với a,b,c∈Za,b,c\in Z . Mệnh đề nào sau đây là đúng?

A.  
a−b+c=0a-b+c=0
B.  
a+b+c=1a+b+c=1
C.  
2a+b+c=−12a+b+c=-1
D.  
a+2b+c=0a+2b+c=0
Câu 41: 1 điểm

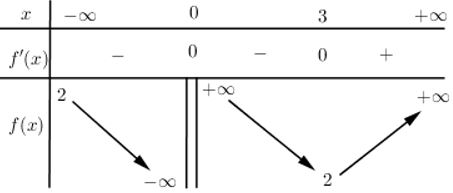
Cho hàm số y=f(x)y=f\left( x \right) xác định và liên tục trên (−∞;0)\left( -\infty ;0 \right) và (0;+∞)\left( 0;+\infty \right) có bảng biến thiên như sau: Mệnh đề nào dưới đây là đúng?

A.  
Đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số.
B.  
Hàm số có giá trị nhỏ nhất bằng 2.
C.  
Hàm số đồng biến trên (2;+∞).\left( 2;+\infty \right).
D.  
f(−3)>f(−2).f\left( -3 \right)>f\left( -2 \right).
Câu 42: 1 điểm

Tìm tất cả các giá trị của x thỏa mãn ∫0xsin⁡2tdt=0\int\limits_{0}^{x}{\sin 2tdt}=0

A.  
x=kπ  (k∈Z)x=k\pi \,\,\left( k\in Z \right)
B.  
x=π2+kπ  (k∈Z)x=\frac{\pi }{2}+k\pi \,\,\left( k\in Z \right)
C.  
x=π4+kπ  (k∈Z)x=\frac{\pi }{4}+k\pi \,\,\left( k\in Z \right)
D.  
x=2kπ  (k∈Z)x=2k\pi \,\,\left( k\in Z \right)
Câu 43: 1 điểm

Trong không gian với hệ tọa độ Oxy, cho hai đường thẳng d:  x1=y−2=z+1−1d:\,\,\frac{x}{1}=\frac{y}{-2}=\frac{z+1}{-1} và d′:  x−1−2=y−24=z2d':\,\,\frac{x-1}{-2}=\frac{y-2}{4}=\frac{z}{2} . Viết phương trình mặt phẳng (Q) chứa hai đường thẳng d và d’.

A.  
(Q):  y−2z−2=0\left( Q \right):\,\,y-2z-2=0
B.  
(Q):  x−y−2=0\left( Q \right):\,\,x-y-2=0
C.  
Không tồn tại (Q)\left( Q \right)
D.  
(Q):  −2y+4z+1=0\left( Q \right):\,\,-2y+4z+1=0
Câu 44: 1 điểm

Cho hàm số y=x3+x2−5x+1y={{x}^{3}}+{{x}^{2}}-5x+1 . Viết phương trình tiếp tuyến của đồ thị hàm số đã cho tại điểm có hoành độ x = 2.

A.  
y=11x−19y=11x-19
B.  
y=−10x+8y=-10x+8
C.  
y=11x+10y=11x+10
D.  
y=10x+9y=10x+9
Câu 45: 1 điểm

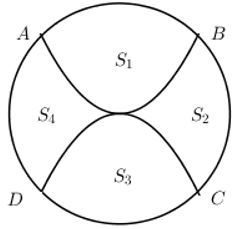
Sân trường THPT Chuyên Hà Giang có một bồn hoa hình tròn có tâm O. Một nhóm học sinh lớp 12 được giao thiết kế bồn hoa, nhóm này chia bồn hoa thành bốn phần, bởi hai đường Parabol có cùng đỉnh O và đối xứng nhau qua O. Hai đường Parabol này cắt đường tròn tại bốn điểm A, B, C, D tạo thành một hình vuông có cạnh bằng 4m (như hình vẽ). Phần diện tích S1, S2 dùng để trồng hoa, phần diện tích S3, S4 dùng để trồng cỏ (Diện tích được làm tròn đến hàng phần trăm). Biết kinh phí trồng hoa là 150.000 đồng/ 1 m2, kinh phí trồng cỏ là 100.000 đồng/1m2. Hỏi cả trường cần bao nhiêu tiền để trồng bồn hoa đó? (Số tiền làm tròn đến hàng chục nghìn).

A.  
3.000.000 đồng
B.  
6.060.000 đồng
C.  
3.270.000 đồng
D.  
5.790.000 đồng
Câu 46: 1 điểm

Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều cạnh bằng 4. Hình chiếu vuông góc của A’ trên (ABC) trùng với tâm O của đường tròn ngoại tiếp tam giác ABC. Gọi M là trung điểm của cạnh AC, tính khoảng cách d giữa hai đường thẳng BM và B’C.

A.  
d=2d=\sqrt{2}
B.  
d=2d=2
C.  
d=1d=1
D.  
d=22d=2\sqrt{2}
Câu 47: 1 điểm

Cho dãy số (un)\left( {{u}_{n}} \right) xác định bởi . Tìm số nguyên n nhỏ nhất để un>2018.{{u}_{n}}>2018.

A.  
n = 10
B.  
n = 9
C.  
n = 11
D.  
n = 8
Câu 48: 1 điểm

Tìm giá trị lớn nhất của hàm số y=x+1+3−xy=\sqrt{x+1}+\sqrt{3-x}

A.  
max⁡[−1;3] f(x)=23\underset{\left[ -1;3 \right]}{\mathop{\max }}\,f\left( x \right)=2\sqrt{3}
B.  
max⁡[−1;3] f(x)=22\underset{\left[ -1;3 \right]}{\mathop{\max }}\,f\left( x \right)=2\sqrt{2}
C.  
max⁡[−1;3] f(x)=2\underset{\left[ -1;3 \right]}{\mathop{\max }}\,f\left( x \right)=2
D.  
max⁡[−1;3] f(x)=32\underset{\left[ -1;3 \right]}{\mathop{\max }}\,f\left( x \right)=3\sqrt{2}
Câu 49: 1 điểm

Trong mặt phẳng phức gọi A, B, C lần lượt là các điểm biểu diễn các số phức z1=(1−i)(2+i),  z2=1+3i;  z3=−1−3i.{{z}_{1}}=\left( 1-i \right)\left( 2+i \right),\,\,{{z}_{2}}=1+3i;\,\,{{z}_{3}}=-1-3i. Tam giác ABC là

A.  
Một tam giác đều.
B.  
Một tam giác vuông cân.
C.  
Một tam giác vuông (không cân).
D.  
Một tam giác cân (không đều, không vuông).
Câu 50: 1 điểm

Đồ thị hàm số y=2x−1y=\frac{2}{x-1} có bao nhiêu đường tiệm cận?

A.  
2
B.  
0
C.  
3
D.  
1

Xem thêm đề thi tương tự

thumbnail
[2022] Trường THPT Tân Bình - Đề thi thử THPT QG năm 2022 môn Vật Lý
Chưa có mô tả

40 câu hỏi 1 mã đề 1 giờ

195,778 lượt xem 105,413 lượt làm bài

Bạn chưa chinh phục đề thi này!!!
thumbnail
[2022] Trường THPT Tân Tạo A - Đề thi thử THPT QG năm 2022 môn Sinh Học
Chưa có mô tả

40 câu hỏi 1 mã đề 1 giờ

205,201 lượt xem 110,488 lượt làm bài

Bạn chưa chinh phục đề thi này!!!
thumbnail
[2022] Trường THPT Duy Tân - Đề thi thử THPT QG năm 2022 môn Sinh
Chưa có mô tả

40 câu hỏi 1 mã đề 1 giờ

220,438 lượt xem 118,692 lượt làm bài

Bạn chưa chinh phục đề thi này!!!
thumbnail
[2022] Trường THPT Lê Trọng Tấn - Đề thi thử THPT QG năm 2022 môn Tiếng Anh
Chưa có mô tả

50 câu hỏi 1 mã đề 1 giờ

213,922 lượt xem 115,185 lượt làm bài

Bạn chưa chinh phục đề thi này!!!
thumbnail
[2022] Trường THPT Long Trường - Đề thi thử THPT QG năm 2022 môn Toán
Chưa có mô tả

50 câu hỏi 1 mã đề 1 giờ

193,597 lượt xem 104,237 lượt làm bài

Bạn chưa chinh phục đề thi này!!!
thumbnail
[2022] Trường THPT Chuyên Lê Hồng Phong - Đề thi thử THPT QG năm 2022 môn Tiếng Anh
Chưa có mô tả

50 câu hỏi 1 mã đề 1 giờ

214,057 lượt xem 115,255 lượt làm bài

Bạn chưa chinh phục đề thi này!!!
thumbnail
[2022] Trường THPT Chuyên Lê Hồng Phong - Đề thi thử THPT QG năm 2022 môn Sinh Học
Chưa có mô tả

40 câu hỏi 1 mã đề 1 giờ

193,284 lượt xem 104,069 lượt làm bài

Bạn chưa chinh phục đề thi này!!!
thumbnail
[2022] Trường THPT Phong Điền - Đề thi thử THPT QG năm 2022 môn Hóa học
Chưa có mô tả

40 câu hỏi 1 mã đề 1 giờ

202,482 lượt xem 109,025 lượt làm bài

Bạn chưa chinh phục đề thi này!!!
thumbnail
[2022] Trường THPT Chuyên Lê Hồng Phong - Đề thi thử THPT QG năm 2022 môn Hóa học
Chưa có mô tả

40 câu hỏi 1 mã đề 1 giờ

219,019 lượt xem 117,929 lượt làm bài

Bạn chưa chinh phục đề thi này!!!