Trang chủ Đề thi THPT Quốc gia Toán [2022] Trường THPT Trần Nguyên Hãn - Đề thi thử THPT QG năm 2022 môn Toán
thumbnail

[2022] Trường THPT Trần Nguyên Hãn - Đề thi thử THPT QG năm 2022 môn Toán

Đề thi thử THPT Quốc gia môn Toán năm 2022 của Trường THPT Trần Nguyên Hãn, được biên soạn với các câu hỏi bám sát cấu trúc đề thi chính thức. Nội dung bao gồm logarit, hàm số, và tích phân, kèm đáp án chi tiết.

Từ khoá: Toán học logarit hàm số tích phân năm 2022 Trường THPT Trần Nguyên Hãn đề thi thử đề thi có đáp án

Thời gian làm bài: 1 giờ

Đề thi nằm trong bộ sưu tập: 📘 Tuyển Tập Bộ 500 Đề Thi Ôn Luyện Môn Toán THPT Quốc Gia Các Tỉnh Từ Năm 2018-2025 - Có Đáp Án Chi Tiết


Bạn chưa làm đề thi này!!!

Hãy bắt đầu chinh phục nào!



 

Xem trước nội dung:

Câu 1: 1 điểm

Cho hàm số y=f(x)y = f\left( x \right) liên tục trên R\mathbb{R} và có đồ thị như hình vẽ dưới. Hỏi hàm số đó có bao nhiêu điểm cực trị?

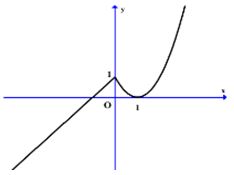
Hình ảnh

A.  
00
B.  
33
C.  
11
D.  
22
Câu 2: 1 điểm

Cho tứ diện ABCDABCD có AB,AC,ADAB,AC,AD đôi một vuông góc, AB=4cm,AC=5cm,AD=3cm.AB = 4cm,AC = 5cm,AD = 3cm. Thể tích khối tứ diện ABCDABCD bằng:

A.  
15cm3.15c{m^3}.
B.  
10cm3.10c{m^3}.
C.  
60cm3.60c{m^3}.
D.  
20cm3.20c{m^3}.
Câu 3: 1 điểm

Cho hàm số y=f(x)y = f\left( x \right) xác định, liên tục trên R\mathbb{R} và có đồ thị như hình vẽ dưới đây. Mệnh đề nào sau đây đúng?

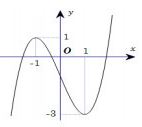
Hình ảnh

A.  
Hàm số đồng biến trên khoảng (−∞;1)\left( { - \infty ; 1} \right) .
B.  
Hàm số đồng biến trên khoảng (−∞;−1)\left( { - \infty ; - 1} \right) .
C.  
Hàm số đồng biến trên khoảng (0;+∞).\left( {0; + \infty } \right).
D.  
Hàm số đồng biến trên khoảng (−3;+∞).\left( { - 3; + \infty } \right).
Câu 4: 1 điểm

Cho hình lăng trụ đứng ABC.A′B′C′ABC.A'B'C' có đáy là tam giác đều cạnh a,a,A′BA'B tạo với mặt phẳng đáy góc 60∘.{60^ \circ }. Thể tích khối lăng trụ ABC.A′B′C′ABC.A'B'C' bằng

A.  
3a32.\frac{{3{a^3}}}{2}.
B.  
a34.\frac{{{a^3}}}{4}.
C.  
3a34.\frac{{3{a^3}}}{4}.
D.  
3a38.\frac{{3{a^3}}}{8}.
Câu 5: 1 điểm

Biết phương trình log⁡52x+1x=2log⁡3(x2−12x){\log _5}\frac{{2\sqrt x + 1}}{x} = 2{\log _3}\left( {\frac{{\sqrt x }}{2} - \frac{1}{{2\sqrt x }}} \right) có một nghiệm dạng x=a+b2x = a + b\sqrt 2 trong đó a,ba,b là các số nguyên. Tính 2a+b2a + b .

A.  
3.3.
B.  
8.8.
C.  
4.4.
D.  
5.5.
Câu 6: 1 điểm

Cho số dương aa và m,n∈Rm,n \in \mathbb{R} . Mệnh đề nào sau đây đúng?

A.  
am.an=am−n.{a^m}.{a^n} = {a^{m - n}}.
B.  
am.an=(am)n.{a^m}.{a^n} = {({a^m})^n}.
C.  
am.an=am+n.{a^m}.{a^n} = {a^{m + n}}.
D.  
am.an=amn.{a^m}.{a^n} = {a^{mn}}.
Câu 7: 1 điểm

Cho hình chóp S.ABCDS.ABCD có đáy là hình thang cân với đáy AB=2a,  AD=BC=CD=a,AB = 2a,\,\,AD = BC = CD = a, mặt bên SABSAB là tam giác cân đỉnh SS và nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD).\left( {ABCD} \right). Biết khoảng cách từ AA tới mặt phẳng (SBC)\left( {SBC} \right) bằng 2a155,\frac{{2a\sqrt {15} }}{5}, tính theo aa thể tích VV của khối chóp S.ABCD.S.ABCD.

A.  
V=3a334.V = \frac{{3{a^3}\sqrt 3 }}{4}.
B.  
V=3a34.V = \frac{{3{a^3}}}{4}.
C.  
V=3a354.V = \frac{{3{a^3}\sqrt 5 }}{4}.
D.  
V=3a328.V = \frac{{3{a^3}\sqrt 2 }}{8}.
Câu 8: 1 điểm

Gọi R,l,hR,l,h lần lượt là bán kính đáy, độ dài đường sinh, chiều cao của hình nón (N).\left( N \right). Diện tích xung quanh Sxq{S_{xq}} của hình nón là

A.  
Sxq=πRh.{S_{xq}} = \pi Rh.
B.  
Sxq=2πRh.{S_{xq}} = 2\pi Rh.
C.  
Sxq=2πRl.{S_{xq}} = 2\pi Rl.
D.  
Sxq=πRl.{S_{xq}} = \pi Rl.
Câu 9: 1 điểm

Tìm điểm cực đại x0{x_0} của hàm số y=x3−3x+1y = {x^3} - 3x + 1 .

A.  
x0=1.{x_0} = 1.
B.  
x0=2.{x_0} =2.
C.  
x0=−1.{x_0} = - 1.
D.  
x0=3.{x_0} = 3.
Câu 10: 1 điểm

Biết rằng hàm số f(x)=x3−3x2−9x+28f\left( x \right) = {x^3} - 3{x^2} - 9x + 28 đạt giá trị nhỏ nhất trên đoạn [0;4]\left[ {0;4} \right] tại x0{x_0} . Tính P=x0+2018.P = {x_0} + 2018.

A.  
P=2021.P = 2021.
B.  
P=2018.P = 2018.
C.  
P=2019.P = 2019.
D.  
P=3.P = 3.
Câu 11: 1 điểm

Cho hàm số f(x)=ax4+bx3+cx2+dx+ef\left( x \right) = a{x^4} + b{x^3} + c{x^2} + dx + e(ae0)\left( {a e 0} \right) . Biết rằng hàm số f(x)f\left( x \right) có đạo hàm là f′(x)f'\left( x \right) và hàm số y=f′(x)y = f'\left( x \right) có đồ thị như hình vẽ dưới. Khi đó mệnh đề nào sau đây sai?

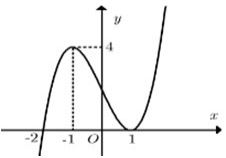
Hình ảnh

A.  
Hàm số f(x)f\left( x \right) nghịch biến trên khoảng (−1;1).\left( { - 1;1} \right).
B.  
Hàm số f(x)f\left( x \right) đồng biến trên khoảng (0;+∞)\left( {0; + \infty } \right) .
C.  
Hàm số f(x)f\left( x \right) đồng biến trên khoảng (−2;1)\left( { - 2;1} \right) .
D.  
Hàm số f(x)f\left( x \right) nghịch biến trên khoảng (−∞;−2)\left( { - \infty ; - 2} \right) .
Câu 12: 1 điểm

Cho khối lăng trụ ABC.A′B′C′ABC.A'B'C' có thể tích bằng 72cm3.72c{m^3}. Gọi MM là trung điểm của đoạn thẳng BB′.BB'. Tính thể tích khối tứ diện ABCM.ABCM.

A.  
36cm3.36c{m^3}.
B.  
18cm3.18c{m^3}.
C.  
24cm3.24c{m^3}.
D.  
12cm3.12c{m^3}.
Câu 13: 1 điểm

Đường cong trong hình dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ?

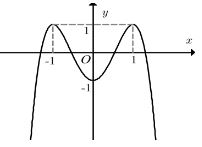
Hình ảnh

A.  
y=−2x4+4x2−1.y = - 2{x^4} + 4{x^2} - 1.
B.  
y=x4−2x2−1.y = {x^4} - 2{x^2} - 1.
C.  
y=−x4+4x2−1.y = - {x^4} + 4{x^2} - 1.
D.  
y=−x4+2x2+1.y = - {x^4} + 2{x^2} + 1.
Câu 14: 1 điểm

Một cái cốc hình trụ có bán kính đáy là 2 cm2\,cm , chiều cao 20 cm20\,cm . Trong cốc đang có một ít nước, khoảng cách giữa đáy cốc và mặt nước là 12 cm12\,cm (Hình vẽ). Một con quạ muốn uống được nước trong cốc thì mặt nước phải cách miệng cốc không quá 6 cm6\,cm . Con quạ thông minh mổ những viên bi đá hình cầu có bán kính 0,6 cm0,6\,cm thả vào cốc nước để mực nước dâng lên. Để uống được nước thì con quạ cần thả vào cốc ít nhất bao nhiêu viên bi?

A.  
2929
B.  
3030
C.  
2828
D.  
2727
Câu 15: 1 điểm

Giả sử m=−ab,a,b∈Z+,(a,b)=1m = - \frac{a}{b},{\rm{ }}a,b \in {\mathbb{Z}^ + },\left( {a,b} \right) = 1 là giá trị thực của tham số mm để đường thẳng d: y = −3x + md:\,y\, = \, - 3x\, + \,m cắt đồ thị hàm số y = 2x + 1x − 1y\, = \,\frac{{2x\, + \,1}}{{x\, - \,1}}(C)\left( C \right) tại hai điểm phân biệt A,BA,B sao cho trọng tâm tam giác OABOAB thuộc đường thẳng Δ : x − 2y − 2 = 0\Delta \,:\,x\, - \,2y\, - \,2\, = \,0 , với OO là gốc tọa độ. Tính a+2b.a + 2b.

A.  
22
B.  
55
C.  
1111
D.  
2121
Câu 16: 1 điểm

Phương trình (2x−5)(log⁡2x−3)=0\left( {{2^x} - 5} \right)\left( {{{\log }_2}x - 3} \right) = 0 có hai nghiệm x1,x2{x_1},{x_2} (với {x_1} < {x_2} ). Tính giá trị của biểu thức K=x1+3x2K = {x_1} + 3{x_2} .

A.  
K=18+log⁡25.K = 18 + {\log _2}5.
B.  
K=20+log⁡25.K = 20 + {\log _2}5.
C.  
K=24+log⁡25.K = 24 + {\log _2}5.
D.  
K=32+log⁡23.K = 32 + {\log _2}3.
Câu 17: 1 điểm

Cho f(1)=1,f(m+n)=f(m)+f(n)+mnf(1) = 1,f(m + n) = f(m) + f(n) + mn với mọi m,n∈N∗m,n \in {N^*} . Tính giá trị của biểu thức T=log⁡[f(96)−f(69)−2412]T = \log \left[ {\frac{{f(96) - f(69) - 241}}{2}} \right] .

A.  
99
B.  
33
C.  
1010
D.  
44
Câu 18: 1 điểm

Tính giá trị của biểu thức P=(4+23)2018.(1−3)2017(1+3)2019P = \frac{{{{\left( {4 + 2\sqrt 3 } \right)}^{2018}}.{{\left( {1 - \sqrt 3 } \right)}^{2017}}}}{{{{\left( {1 + \sqrt 3 } \right)}^{2019}}}} .

A.  
P=−22017.P = - {2^{2017}}.
B.  
P=−1.P = - 1.
C.  
P=−22019.P = - {2^{2019}}.
D.  
P=22018.P = {2^{2018}}.
Câu 19: 1 điểm

Một hình trụ có hai đáy là hai hình tròn (O;r)\left( {O;r} \right) và (O′;r).\left( {O';r} \right). Khoảng cách giữa hai đáy là OO′=r3.OO' = r\sqrt 3 . Một hình nón có đỉnh là OO và có đáy là hình tròn (O′;r).\left( {O';r} \right). Gọi S1{S_1} là diện tích xung quanh của hình trụ và S2{S_2} là diện tích xung quanh của hình nón. Tính tỉ số S1S2.\frac{{{S_1}}}{{{S_2}}}.

A.  
S1S2=23.\frac{{{S_1}}}{{{S_2}}} = \frac{2}{{\sqrt 3 }}.
B.  
S1S2=23.\frac{{{S_1}}}{{{S_2}}} = 2\sqrt 3 .
C.  
S1S2=2.\frac{{{S_1}}}{{{S_2}}} = 2.
D.  
S1S2=3.\frac{{{S_1}}}{{{S_2}}} = \sqrt 3 .
Câu 20: 1 điểm

Anh Nam mới ra trường và đi làm với mức lương khởi điểm là 6 triệu đồng/1tháng. Anh muốn dành một khoản tiền tiết kiệm bằng cách trích ra 20% lương hàng tháng gửi vào ngân hàng theo hình thức lãi kép với lãi suất 0,5%/ tháng. Hỏi sau một năm, số tiền tiết kiệm của anh Nam gần nhất với số nào sau đây?

A.  
15 320 000 đồng
B.  
14 900 000 đồng.
C.  
14 880 000 đồng.
D.  
15 876 000 đồng.
Câu 21: 1 điểm

Biết rằng đồ thị hàm số y=x3−4x2+5x−1y = {x^3} - 4{x^2} + 5x - 1 cắt đồ thị hàm số y=1y = 1 tại hai điểm phân biệt AA và BB . Tính độ dài đoạn thẳng AB.AB.

A.  
AB=2.AB = 2.
B.  
AB=3.AB = 3.
C.  
AB=22.AB = 2\sqrt 2 .
D.  
AB=1.AB = 1.
Câu 22: 1 điểm

Cho khối chóp có thể tích bằng 32cm332c{m^3} và diện tích đáy bằng 16cm2.16c{m^2}. Chiều cao của khối chóp đó là

A.  
4cm.4cm.
B.  
6cm.6cm.
C.  
3cm.3cm.
D.  
2cm.2cm.
Câu 23: 1 điểm

Giải phương trình log⁡3(x−1)=2.{\log _3}\left( {x - 1} \right) = 2.

A.  
x=10.x = 10.
B.  
x=11.x = 11.
C.  
x=8.x = 8.
D.  
x=7.x = 7.
Câu 24: 1 điểm

Cho hình chóp S.ABCS.ABC có SA=2a,SB=3a,SC=4aSA = 2a,SB = 3a,SC = 4a và ASB^=BSC^=60∘,ASC^=90∘.\widehat {ASB} = \widehat {BSC} = {60^ \circ },\widehat {ASC} = {90^ \circ }. Tính thể tích VV của khối chóp S.ABC.S.ABC.

A.  
V=2a329.V = \frac{{2{a^3}\sqrt 2 }}{9}.
B.  
V=2a32.V = 2{a^3}\sqrt 2 .
C.  
V=4a323.V = \frac{{4{a^3}\sqrt 2 }}{3}.
D.  
V=a32.V = {a^3}\sqrt 2 .
Câu 25: 1 điểm

Phương trình tiếp tuyến của đồ thị hàm số y=f(x)=(x2−1)2y = f(x) = {({x^2} - 1)^2} tại điểm M(2;9)M(2;9) là

A.  
y=6x−3.y = 6x - 3.
B.  
y=8x−7.y = 8x - 7.
C.  
y=24x−39.y = 24x - 39.
D.  
y=6x+21.y = 6x + 21.
Câu 26: 1 điểm

Cho hình nón có chiều cao bằng 8cm,8cm, bán kính đáy bằng 6cm.6cm. Diện tích toàn phần của hình nón đã cho bằng

A.  
116π cm2.116\pi \,c{m^2}.
B.  
84π cm2.84\pi \,c{m^2}.
C.  
96π cm2.96\pi \,c{m^2}.
D.  
132π cm2.132\pi \,c{m^2}.
Câu 27: 1 điểm

Cho hàm số y=x+22x+3y = \frac{{x + 2}}{{2x + 3}} có đồ thị (C)(C) . Đường thẳng dd có phương trình y=ax+by = ax + b là tiếp tuyến của (C)(C) , biết dd cắt trục hoành tại AA và cắt trục tung tại BB sao cho tam giác OABOAB cân tại OO , với OO là gốc tọa độ. Tính a+ba + b .

A.  
−1. - 1.
B.  
−2. - 2.
C.  
0.0.
D.  
−3. - 3.
Câu 28: 1 điểm

Cho a > 0 và ae1a e 1 . Tìm mệnh đề đúng trong các mệnh đề sau.

A.  
log⁡axn=nlog⁡ax{\log _a}{x^n} = n{\log _a}x (với x>0x > 0 ).
B.  
log⁡axy=log⁡axlog⁡ay.{\log _a}\frac{x}{y} = \frac{{{{\log }_a}x}}{{{{\log }_a}y}}. (với x>0,y>0x > 0,y > 0 ).
C.  
log⁡ax{\log _a}x có nghĩa với mọi xx .
D.  
log⁡a1=a,log⁡aa=1{\log _a}1 = a,{\log _a}a = 1 .
Câu 29: 1 điểm

Cho hàm số y=f(x)y = f\left( x \right) liên tục trên R\mathbb{R} và có đồ thị như hình vẽ dưới. Xét hàm số g(x)=f(2x3+x−1)+m.g\left( x \right) = f\left( {2{x^3} + x - 1} \right) + m. Tìm mm để max⁡[0;1]g(x)=−10.\mathop {\max }\limits_{\left[ {0;1} \right]} g\left( x \right) = - 10.

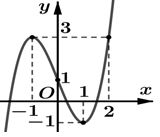
Hình ảnh

A.  
m=−13.m = - 13.
B.  
m=5.m = 5.
C.  
m=3.m = 3.
D.  
m=−1.m = - 1.
Câu 30: 1 điểm

Có tất cả bao nhiêu giá trị nguyên của tham số mm thuộc đoạn [−2018;2019]\left[ { - 2018;2019} \right] để hàm số y=mx4+(m+1)x2+1y = m{x^4} + \left( {m + 1} \right){x^2} + 1 có đúng một điểm cực đại?

A.  
00
B.  
20182018
C.  
11
D.  
2019.2019.
Câu 31: 1 điểm

Cho hàm số y=f(x)y = f\left( x \right) có bảng biến thiên như sau:

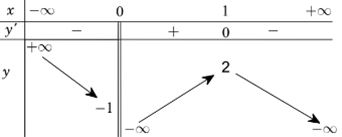
Hình ảnh

Tìm tất cả các giá trị thực của tham số mm sao cho phương trình f(x)=mf\left( x \right) = m có đúng hai nghiệm.

A.  
m<−1m < - 1 , m=2.m = 2.
B.  
m≤−1m \le - 1 , m=2.m = 2.
C.  
m≤2.m \le 2.
D.  
m<2.m < 2.
Câu 32: 1 điểm

Hàm số f(x)=22xf(x) = {2^{2x}} có đạo hàm

A.  
f′(x)=22xln⁡2.f'(x) = {2^{2x}}\ln 2.
B.  
f′(x)=22x−1.f'(x) = {2^{2x - 1}}.
C.  
f′(x)=22x+1ln⁡2.f'(x) = {2^{2x + 1}}\ln 2.
D.  
f′(x)=2x22x−1.f'(x) = 2x{2^{2x - 1}}.
Câu 33: 1 điểm

Cho hình chóp S.ABC có đáy ABC là tam giác với AB=2cm,AC=3cm,  ∠BAC=600,SA⊥(ABC).AB = 2cm,AC = 3cm,\;\angle BAC = {60^0},SA \bot \left( {ABC} \right). Gọi B1,C1{B_1},{C_1} lần lượt là hình chiếu vuông góc của A lên SB, SC. Tính thể tích khối cầu đi qua năm điểm A,B,C,B1,C1.A,B,C,{B_1},{C_1}.

A.  
2821π27cm3.\frac{{28\sqrt {21} \pi }}{{27}}c{m^3}.
B.  
7657π27cm3.\frac{{76\sqrt {57} \pi }}{{27}}c{m^3}.
C.  
77π6cm3.\frac{{7\sqrt 7 \pi }}{6}c{m^3}.
D.  
27π6cm3.\frac{{27\pi }}{6}c{m^3}.
Câu 34: 1 điểm

Cho hàm số f(x)=x−m2x+8f\left( x \right) = \frac{{x - {m^2}}}{{x + 8}} với mm là tham số thực. Giả sử m0{m_0} là giá trị dương của tham số mm để hàm số có giá trị nhỏ nhất trên đoạn [0;3]\left[ {0;3} \right] bằng −3 - 3 . Giá trị m0{m_0} thuộc khoảng nào trong các khoảng cho dưới đây?

A.  
(2;5).\left( {2;5} \right).
B.  
(1;4).\left( {1;4} \right).
C.  
(6;9).\left( {6;9} \right).
D.  
(20;25).\left( {20;25} \right).
Câu 35: 1 điểm

Sau một tháng thi công dãy phòng học của Trường X, công ty xây dựng đã thực hiện được một khối lượng công việc. Nếu tiếp tục với tiến độ như vậy thì dự kiến sau đúng 2525 tháng nữa công trình sẽ hoàn thành. Để kịp thời đưa công trình vào sử dụng, công ty xây dựng quyết định từ tháng thứ 22 , mỗi tháng tăng 5%5\% khối lượng công việc so với tháng kề trước. Hỏi công trình sẽ hoàn thành ở tháng thứ mấy sau khi khởi công?

A.  
1919
B.  
1818
C.  
1717
D.  
1616
Câu 36: 1 điểm

Cho hình chóp S.ABCDS.ABCD có đáy ABCDABCD là hình bình hành. Gọi K,MK,M lần lượt là trung điểm của các đoạn thẳng SA,SB,   (α)SA,SB,\,\,\,\left( \alpha \right) là mặt phẳng qua KK song song với ACAC và AM.AM. Mặt phẳng (α)\left( \alpha \right) chia khối chóp S.ABCDS.ABCD thành hai khối đa diện. Gọi V1{V_1} là thể tích của khối đa diện chứa đỉnh SS và V2{V_2} là thể tích khối đa diện còn lại. Tính tỉ số V1V2.\frac{{{V_1}}}{{{V_2}}}.

A.  
V1V2=725.\frac{{{V_1}}}{{{V_2}}} = \frac{7}{{25}}.
B.  
V1V2=511.\frac{{{V_1}}}{{{V_2}}} = \frac{5}{{11}}.
C.  
V1V2=717.\frac{{{V_1}}}{{{V_2}}} = \frac{7}{{17}}.
D.  
V1V2=923.\frac{{{V_1}}}{{{V_2}}} = \frac{9}{{23}}.
Câu 37: 1 điểm

Cho hình chóp tứ giác đều có tất cả các cạnh bằng 2a.2a. Bán kính mặt cầu ngoại tiếp hình chóp đã cho bằng a62.\frac{{a\sqrt 6 }}{2}.

A.  
a62.\frac{{a\sqrt 6 }}{2}.
B.  
a2.a\sqrt 2 .
C.  
2a3.\frac{{2a}}{{\sqrt 3 }}.
D.  
a22.\frac{{a\sqrt 2 }}{2}.
Câu 38: 1 điểm

Cho hàm số y=f(x)y = f\left( x \right) có bảng biến thiên như sau:

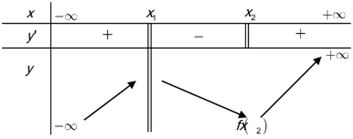
Hình ảnh

Mệnh đề nào sau đây đúng?

A.  
Hàm số đã cho có một điểm cực đại và một điểm cực tiểu.
B.  
Hàm số đã cho không có cực trị.
C.  
Hàm số đã cho có một điểm cực đại và không có điểm cực tiểu.
D.  
Hàm số đã cho có một điểm cực tiểu và không có điểm cực đại.
Câu 39: 1 điểm

Tìm tập xác định của hàm số y=11−ln⁡xy = \frac{1}{{1 - \ln x}} .

A.  
(0;+∞)\{e}.\left( {0; + \infty } \right)\backslash \left\{ e \right\}.
B.  
(e;+∞).\left( {e; + \infty } \right).
C.  
R\{e}.\mathbb{R}\backslash \left\{ e \right\}.
D.  
(0;+∞).\left( {0; + \infty } \right).
Câu 40: 1 điểm

Cho các dạng đồ thị (I), (II), (III) như hình dưới đây:

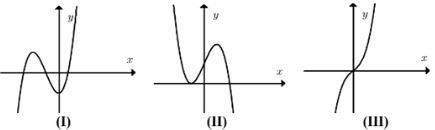
Hình ảnh

Đồ thị hàm số y=x3+bx2−x+d(b,d∈R)y = {x^3} + b{x^2} - x + d{\rm{ }}\left( {b,d \in \mathbb{R}} \right) có thể là dạng nào trong các dạng trên?

A.  
(III)
B.  
(I) và (III)
C.  
(I) và (II)
D.  
(I)
Câu 41: 1 điểm

Mặt cầu có bán kính aa thì có diện tích xung quanh bằng

A.  
43πa2.\frac{4}{3}\pi {a^2}.
B.  
4πa2.4\pi {a^2}.
C.  
2πa.2\pi a.
D.  
πa2.\pi {a^2}.
Câu 42: 1 điểm

Có tất cả bao nhiêu giá trị nguyên của tham số mm để phương trình log⁡2(x−1)=log⁡2(mx−8){\log _{\sqrt 2 }}(x - 1) = {\log _2}(mx - 8) có hai nghiệm thực phân biệt?

A.  
33
B.  
vô số
C.  
44
D.  
55
Câu 43: 1 điểm

Cho hàm số y=ax4+bx2+c(ae0)y = a{x^4} + b{x^2} + c{\rm{ }}\left( {a e 0} \right) có bảng biến thiên dưới đây:

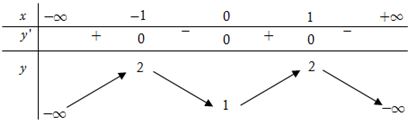
Hình ảnh

Tính P=a−2b+3c.P = a - 2b + 3c.

A.  
P=3.P = 3.
B.  
P=6.P = 6.
C.  
P=−2.P = - 2.
D.  
P=2.P = 2.
Câu 44: 1 điểm

Cho hình chóp S.ABCDS.ABCD có đáy là hình chữ nhật, SASA vuông góc với mặt phẳng (ABCD).\left( {ABCD} \right). Tâm mặt cầu ngoại tiếp hình chóp S.ABCDS.ABCD là điểm II với

A.  
II là trung điểm của đoạn thẳng SD.SD.
B.  
II là trung điểm của đoạn thẳng AC.AC.
C.  
II là trung điểm của đoạn thẳng SC.SC.
D.  
II là trung điểm của đoạn thẳng SB.SB.
Câu 45: 1 điểm

Cho khối chóp tứ giác đều S.ABCDS.ABCD có thể tích bằng a3{a^3} và đáy ABCDABCD là hình vuông cạnh a.a. Tính cos⁡α\cos \alpha với α\alpha là góc giữa mặt bên và mặt đáy.

A.  
cos⁡α=15.\cos \alpha = \frac{1}{{\sqrt 5 }}.
B.  
cos⁡α=13.\cos \alpha = \frac{1}{{\sqrt 3 }}.
C.  
cos⁡α=137.\cos \alpha = \frac{1}{{\sqrt {37} }}.
D.  
cos⁡α=119.\cos \alpha = \frac{1}{{\sqrt {19} }}.
Câu 46: 1 điểm

Cho khối trụ có thể tích bằng 45π cm3,45\pi \,c{m^3}, chiều cao bằng 5cm.5cm. Tính bán kính RR của khối trụ đã cho.

A.  
R=3cm.R = 3cm.
B.  
R=4,5cm.R = 4,5cm.
C.  
R=9cm.R = 9cm.
D.  
R=33cm.R = 3\sqrt 3 cm.
Câu 47: 1 điểm

Cho hình chóp tứ giác S.ABCDS.ABCD có đáy ABCDABCD là hình vuông cạnh bằng a, SA⊥(ABC) , SA=3a.a,\,SA \bot \left( {ABC} \right)\,,\,SA = 3a. Thể tích VV của khối chóp S.ABCDS.ABCD là

A.  
V=2a3V = 2{a^3}
B.  
V=3a3V = 3{a^3}
C.  
V=13a3V = \frac{1}{3}{a^3}
D.  
V=a3V = {a^3}
Câu 48: 1 điểm

Giá trị nhỏ nhất của hàm số y=xex+1y = x{e^{x + 1}} trên [−2;0]\left[ { - 2;0} \right] bằng

A.  
e2{e^2}
B.  
−2e - \frac{2}{e}
C.  
−1 - 1
D.  
00
Câu 49: 1 điểm

Cho cấp số nhân (un)\left( {{u_n}} \right) có công bội dương và u2=14, u4=4.{u_2} = \frac{1}{4},\,{u_4} = 4. Giá trị của u1{u_1} là

A.  
u1=16{u_1} = \frac{1}{6}
B.  
u1=116{u_1} = \frac{1}{{16}}
C.  
u1=12{u_1} = \frac{1}{2}
D.  
u1=−116{u_1} = - \frac{1}{{16}}
Câu 50: 1 điểm

Cho hàm số y=f(x)y = f\left( x \right) xác định, liên tục trên R\{1}\mathbb{R}\backslash \left\{ 1 \right\} và có bảng biến thiên như hình dưới đây

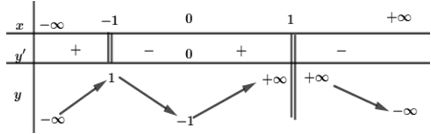
Hình ảnh

Tập hợp SS tất cả các giá trị của m đề phương trình f(x)=mf\left( x \right) = m có đúng ba nghiệm thực là

A.  
S=(−1;1)S = \left( { - 1;1} \right)
B.  
S={−1;1}S = \left\{ { - 1;1} \right\}
C.  
[−1;1]\left[ { - 1;1} \right]
D.  
S={1}S = \left\{ 1 \right\}

Xem thêm đề thi tương tự

thumbnail
[2022] Trường THPT Trần Khai Nguyên - Đề thi thử THPT QG năm 2022 môn ToánTHPT Quốc giaToán
Đề thi thử THPT Quốc gia môn Toán năm 2022 từ Trường THPT Trần Khai Nguyên, với nội dung được biên soạn kỹ lưỡng. Các câu hỏi bao gồm hàm số, tích phân, và bài toán thực tế, giúp học sinh chuẩn bị hiệu quả cho kỳ thi.

50 câu hỏi 1 mã đề 1 giờ

193,130 lượt xem 103,985 lượt làm bài

Chưa chinh phục!!!
thumbnail
[2022] Trường THPT Trần Khai Nguyên - Đề thi thử THPT QG năm 2022 môn Sinh HọcTHPT Quốc giaSinh học
Đề thi thử THPT QG năm 2022 môn Sinh học của Trường THPT Trần Khai Nguyên. Tài liệu bao gồm hệ thống câu hỏi bám sát chương trình học lớp 12, kèm đáp án chi tiết, hỗ trợ học sinh trong việc củng cố kiến thức và luyện tập kỹ năng làm bài.

40 câu hỏi 1 mã đề 1 giờ

210,197 lượt xem 113,169 lượt làm bài

Chưa chinh phục!!!
thumbnail
[2022] Trường THPT Nguyễn Trân - Đề thi thử THPT QG năm 2022 môn Sinh họcTHPT Quốc giaSinh học
Đề thi thử THPT QG năm 2022 môn Sinh học của Trường THPT Nguyễn Trân. Tài liệu này cung cấp hệ thống câu hỏi lý thuyết và bài tập sát chương trình lớp 12, kèm đáp án và lời giải chi tiết.

40 câu hỏi 1 mã đề 1 giờ

206,241 lượt xem 111,048 lượt làm bài

Chưa chinh phục!!!
thumbnail
[2022-2023] Trường THPT Nguyễn Trân - Đề thi thử tốt nghiệp THPT môn Sinh học năm 2022-2023THPT Quốc giaSinh học
Đề thi thử môn Sinh học năm 2022-2023 của Trường THPT Nguyễn Trân, gồm các câu hỏi bám sát chương trình học lớp 12, kết hợp lý thuyết và bài tập vận dụng. Tài liệu này kèm đáp án chi tiết, giúp học sinh làm quen với định dạng đề thi và nâng cao kỹ năng giải bài.

40 câu hỏi 1 mã đề 1 giờ

221,821 lượt xem 119,427 lượt làm bài

Chưa chinh phục!!!
thumbnail
[2022] Trường THPT Trần Quý Cáp - Đề thi thử THPT QG năm 2022 môn Hóa học
Chưa có mô tả

40 câu hỏi 1 mã đề 1 giờ

208,018 lượt xem 112,000 lượt làm bài

Chưa chinh phục!!!
thumbnail
[2022] Trường THPT Trần Hưng Đạo - Đề thi thử THPT QG năm 2022 môn Sinh
Chưa có mô tả

40 câu hỏi 1 mã đề 1 giờ

210,764 lượt xem 113,477 lượt làm bài

Chưa chinh phục!!!
thumbnail
[2022] Trường THPT Trần Công Bình - Đề thi thử THPT QG năm 2022 môn Vật Lý
Chưa có mô tả

40 câu hỏi 1 mã đề 1 giờ

213,710 lượt xem 115,066 lượt làm bài

Chưa chinh phục!!!
thumbnail
[2022] Trường THPT Trần Bình Trọng - Đề thi thử THPT QG năm 2022 môn Sinh HọcTHPT Quốc giaSinh học
Đề thi thử THPT QG năm 2022 môn Sinh học của Trường THPT Trần Bình Trọng. Bao gồm hệ thống câu hỏi bám sát nội dung chương trình lớp 12, với đáp án chi tiết, hỗ trợ học sinh ôn luyện hiệu quả và chuẩn bị tốt cho kỳ thi tốt nghiệp.

40 câu hỏi 1 mã đề 1 giờ

210,021 lượt xem 113,078 lượt làm bài

Chưa chinh phục!!!
thumbnail
[2022] Trường THPT Trần Suyền - Đề thi thử THPT QG năm 2022 môn Sinh
Chưa có mô tả

40 câu hỏi 1 mã đề 1 giờ

220,784 lượt xem 118,881 lượt làm bài

Chưa chinh phục!!!