
[2021] Trường THPT Nguyễn Thị Minh Khai lần 2 - Đề thi thử THPT QG năm 2021 môn Toán
Từ khoá: Toán học giải tích hình học không gian bài toán thực tế năm 2021 Trường THPT Nguyễn Thị Minh Khai lần 2 đề thi thử đề thi có đáp án
Thời gian làm bài: 1 giờ
Đề thi nằm trong bộ sưu tập: 📘 Tuyển Tập Bộ 500 Đề Thi Ôn Luyện Môn Toán THPT Quốc Gia Các Tỉnh Từ Năm 2018-2025 - Có Đáp Án Chi Tiết
Hãy bắt đầu chinh phục nào!
Xem trước nội dung:
Cho tập hợp A có 20 phần tử. Số tập hợp con có 3 phần tử được thành lập từ A là
Cho cấp số nhân với và . Công bội của cấp số nhân đã cho bằng
Số nghiệm của phương trình là
Thể tích của khối lập phương có cạnh bằng c là
Tập xác định của hàm số là
Khẳng định nào sau đây là đúng?
Một khối lập phương có thể tích bằng . Độ dài cạnh khối lập phương bằng
Tính thể tích V của khối trụ có bán kính đáy và chiều cao đều bằng 2.
Cho khối cầu có thể tích . Bán kính của khối cầu bằng
Cho hàm số f(x) có bảng biến thiên như sau:
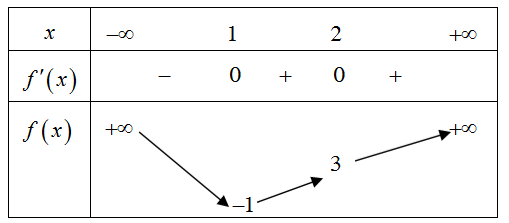
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Với x là số thực dương tùy ý, bằng
Diện tích xung quanh của hình nón có độ dài đường sinh và bán kính đáy là
Cho hàm số xác định và liên tục trên và có bảng biến thiên như sau:
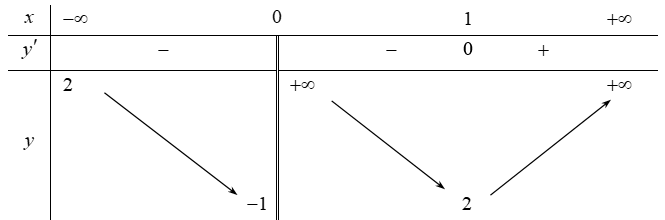
Mệnh đề nào sau đây sai?
Cho hàm số có đồ thị như hình bên.
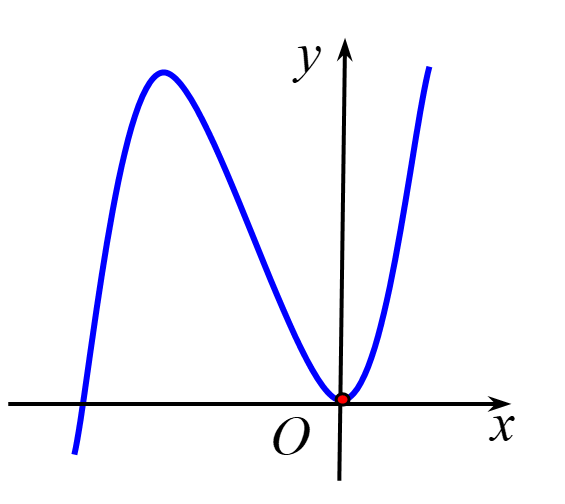
Mệnh đề nào sau đây là đúng?
Tiệm cận ngang của đồ thị hàm số là
Tập nghiệm của bất phương trình là
Cho hàm số bậc ba có đồ thị trong hình dưới. Số nghiệm của phương trình là
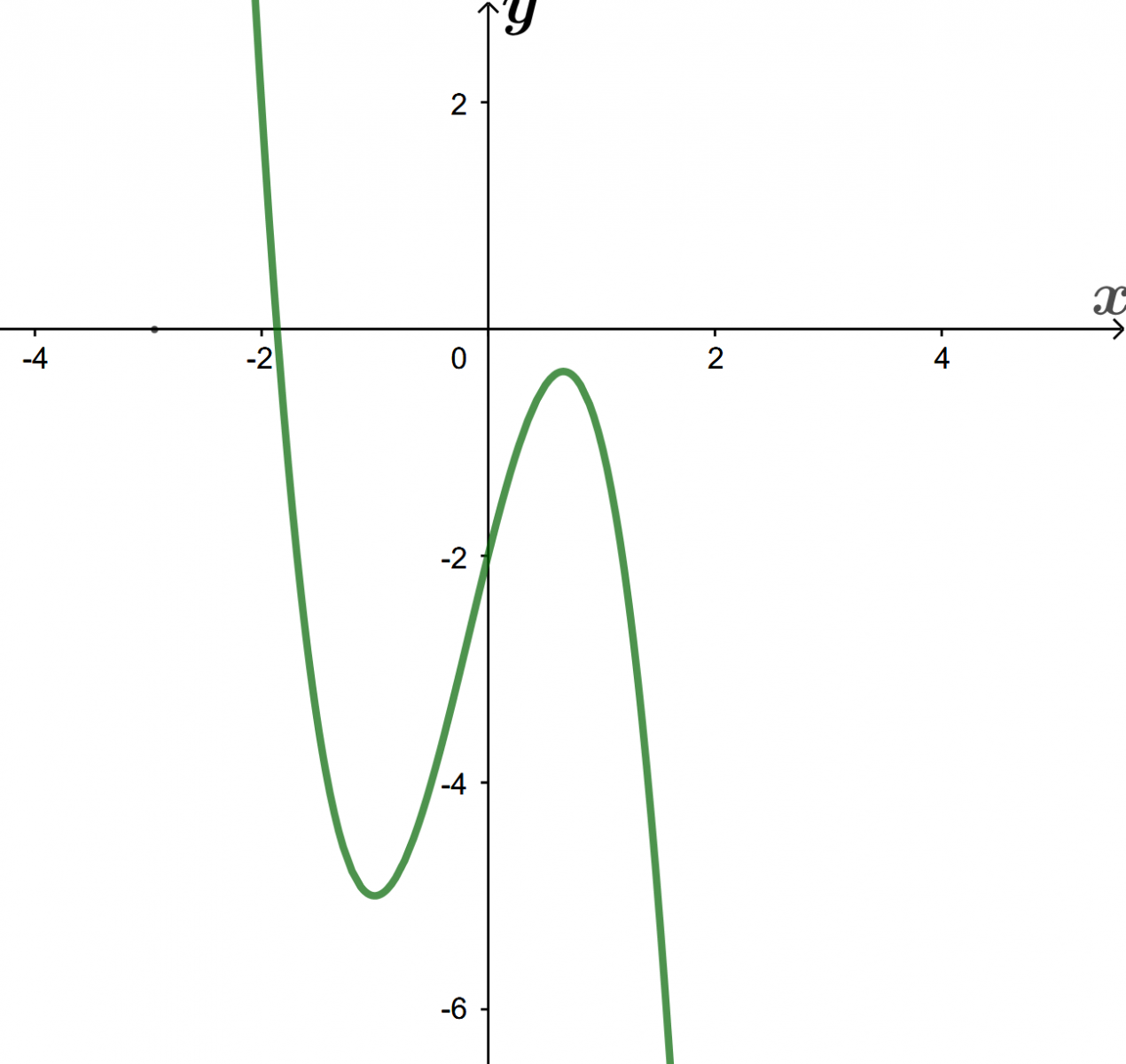
Nếu và thì bằng
Số phức liên hợp của số phức z=3-12i là
Cho hai số phức và . Phần ảo của số phức bằng
Trên mặt phẳng tọa độ (hình vẽ dưới), số phức được biểu diễn bởi điểm nào trong các điểm
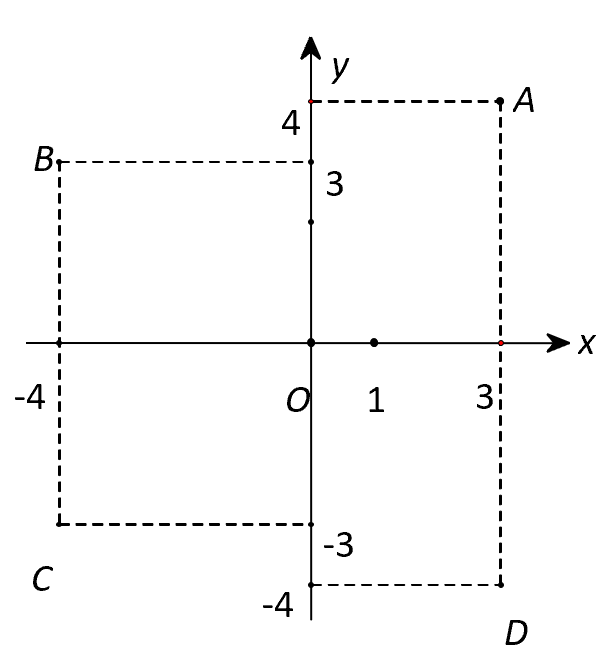
Trong không gian Oxyz, hình chiếu vuông góc của điểm trên trục Ox có toạ độ là
Trong không gian Oxyz, cho mặt cầu Tâm của (S) có tọa độ là
Trong không gian Oxyz, cho mặt phẳng Vectơ nào dưới đây là một vectơ pháp tuyến của
Trong không gian Oxyz, cho đường thẳng . Điểm nào dưới đây thuộc d?
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng , SA=2a, tam giác ABC vuông cân tại C và (minh họa như hình bên).
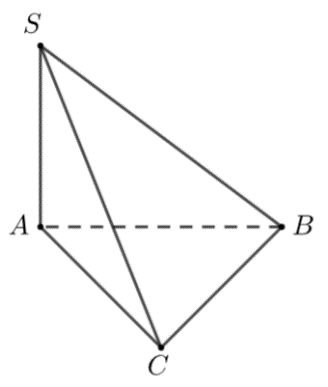
Góc giữa đường thẳng SB và mặt phẳng bằng
Cho hàm số có bảng xét dấu của như sau:
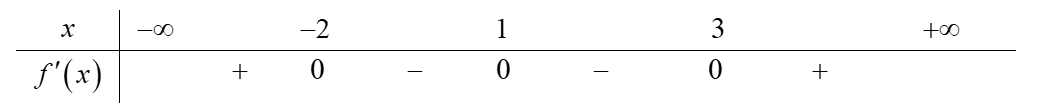
Số điểm cực trị của hàm số đã cho là
Tìm giá trị nhỏ nhất của hàm số trên đoạn .
Cho các số dương a,b,c thỏa mãn . Khẳng định nào sau đây đúng?
Cho hàm số có đồ thị , số giao điểm của đồ thị với trục hoành là
Tập nghiệm của bất phương trình {{4}^{x}}+{{2021.2}^{x}}-2022<0 là
Trong không gian, cho tam giác ABC vuông tại A, , BC=2a. Khi quay tam giác ABC xung quanh cạnh góc vuông AB thì hình tam giác ABC tạo thành một khối nón tròn xoay có thể tích bằng
Xét , nếu đặt thì bằng
Diện tích S của hình phẳng giới hạn bởi các đường và y=6-11x được tính bởi công thức nào dưới đây?
Cho hai số phức và . Phần thực của số phức bằng
Gọi là nghiệm phức có phần ảo dương của phương trình . Môđun của số phức là
Trong không gian Oxyz, cho điểm và đường thẳng . Mặt phẳng đi qua M và vuông góc với có phương trình là
Trong không gian Oxyz, cho điểm và . Đường thẳng MN có phương trình tham số là
Một nhóm 16 học sinh gồm 10 nam trong đó có Bình và 6 nữ trong đó có An được xếp ngẫu nhiên vào 16 ghế trên một hàng ngang để dự lễ khai giảng năm học. Xác suất để xếp được giữa 2 bạn nữ gần nhau có đúng 2 bạn nam, đồng thời Bình không ngồi cạnh An là
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Gọi H là trung điểm AB, G là trọng tâm . Biết và SH=a. Khi đó khoảng cách giữa hai đường thẳng AG và SC là
Có bao nhiêu giá trị nguyên dương của tham số m để hàm số đồng biến trên ?
Một nghiên cứu cho thấy một nhóm học sinh được cho xem cùng một danh sách các loài thực vật và được kiểm tra lại xem họ nhớ được bao nhiêu % mỗi tháng. Sau t tháng, khả năng nhớ trung bình của nhóm học sinh được cho bởi công thức (đơn vị %). Hỏi sau bao lâu nhóm học sinh đó chỉ còn nhớ được dưới 10% của danh sách ?
Cho hàm số (với là các số thực) có đồ thị như hình vẽ dưới đây:
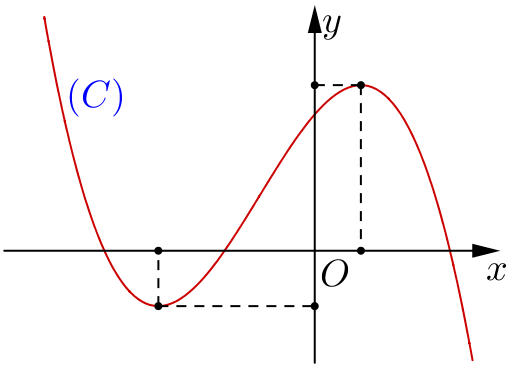
Chọn khẳng định đúng?
Cho hình nón có bán kính đáy bằng 10. Mặt phẳng vuông góc với trục của hình nón cắt hình nón theo một thiết diện là hình tròn có bán kính bằng 6, khoảng cách giữa mặt phẳng với mặt phẳng chứa đáy của hình nón là 5. Diện tích xung quanh của hình nón bằng?
Cho hàm số f(x) thỏa mãn và f(3) = ln3. Tính .
Cho hàm số liên tục trên và có bảng biến thiên như sau:
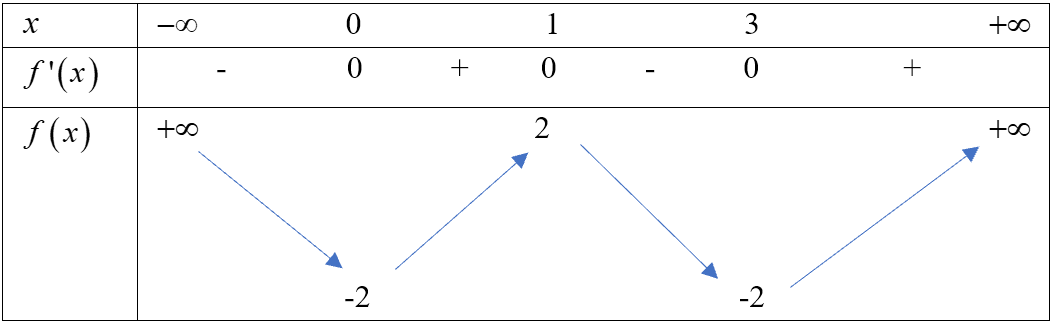
Số nghiệm trong đoạn của phương trình bằng
Cho x,y,\,z>0 ; a,\,b,\,c>1 và . Giá trị lớn nhất của biểu thức thuộc khoảng nào dưới đây?
Cho hàm số (m là tham số thực). Gọi S là tập hợp các giá trị của m sao cho . Tổng các phần tử của S là
Cho hình hộp có diện tích đáy bằng 9, chiều cao bằng 3. Gọi Q,M,N,P,I là những điểm thỏa mãn . Thể tích của khối đa diện lồi có các đỉnh là các điểm Q,M,N,P,I bằng
Cho phương trình . Hỏi có bao nhiêu cặp số nguyên thỏa mãn phương trình trên, biết rằng ?
Xem thêm đề thi tương tự

40 câu hỏi 1 mã đề 1 giờ
206,115 lượt xem 110,978 lượt làm bài

50 câu hỏi 1 mã đề 1 giờ
207,987 lượt xem 111,986 lượt làm bài

1 giờ
207,020 lượt xem 111,468 lượt làm bài

50 câu hỏi 1 mã đề 1 giờ
193,656 lượt xem 104,272 lượt làm bài

Ôn luyện với đề thi giữa học kỳ 2 môn Tiếng Anh lớp 12 năm 2021 từ Trường THPT Nguyễn Thị Diệu. Đề thi bao gồm các câu hỏi về ngữ pháp, từ vựng, kỹ năng đọc hiểu và giao tiếp, kèm đáp án chi tiết giúp học sinh củng cố kiến thức và chuẩn bị tốt cho các kỳ thi học kỳ. Đây là tài liệu hữu ích giúp học sinh lớp 12 ôn tập và đạt kết quả cao. Thi thử trực tuyến miễn phí và hiệu quả.
10 câu hỏi 1 mã đề 50 phút
128,114 lượt xem 68,971 lượt làm bài

50 câu hỏi 1 mã đề 1 giờ
202,314 lượt xem 108,934 lượt làm bài

50 câu hỏi 1 mã đề 1 giờ
215,318 lượt xem 115,934 lượt làm bài

50 câu hỏi 1 mã đề 1 giờ
202,809 lượt xem 109,200 lượt làm bài

50 câu hỏi 1 mã đề 1 giờ
212,627 lượt xem 114,485 lượt làm bài
