Trắc nghiệm Chuyên đề toán 9 Chuyên đề 1: Tam giác đồng dạng, Định lí Talet có đáp án

Cho đoạn thẳng \(AB = 15cm\), M là một điểm trên đoạn thẳng AB sao cho \(\frac{{MA}}{{MB}} = \frac{7}{4}\). Tính độ dài MA và MB.

Tính độ dài x trong các hình sau:

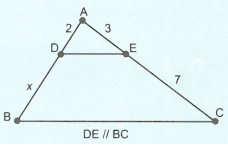
Tính độ dài x trong các hình sau:

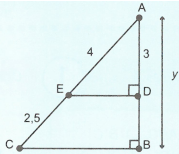
Cho tam giác ABC có \(BC = 15cm\). Trên đường cao AH lấy các điểm I, K sao cho \(AK = KI = IH\). Qua I và K vẽ các đường thẳng EF, MN song song với BC (\(E,M \in AB;F,N \in AC\)). Tính độ dài các đoạn thẳng MN và EF.

Cho tam giác ABC, từ điểm D trên cạnh BC kẻ các đường thẳng song song với các cạnh AB và AC, chúng cắt các cạnh AB và AC theo thứ tự tại E và F.

Chứng minh rằng: \(\frac{{AE}}{{AB}} + \frac{{{\rm{AF}}}}{{AC}} = 1\).

Đường thẳng d cắt các cạnh AB, AD và đường chéo AC của hình bình hành ABCD lần lượt tại E, F và I. Chứng minh rằng \(\frac{{AB}}{{AE}} + \frac{{AD}}{{{\rm{AF}}}} = \frac{{AC}}{{AI}}\).

Chứng minh rằng \[\frac{{D'E}}{{ED}} + \frac{{EC'}}{{EC}} = 1\].

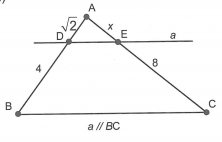
Tính độ dài x, y trong hình sau:

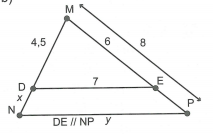
Tính độ dài x, y trong hình sau:

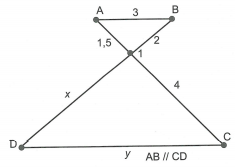
Tính độ dài x, y trong hình sau:

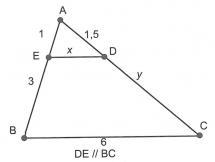
Cho hình thang ABCD \[(AB\parallel CD)\]. Đường thẳng song song với hai đáy cắt cạnh AD tại M, cắt cạnh BC tại N sao cho \[MD = 3MA\]. Cho \[AB = 8\,cm,\,\,CD = 20\,cm\]. Tính MN

Cho tam giác ABC một đường thẳng song song với cạnh BC cắt AB tại D và AC tại E. Trên tia đối của tia CA lấy điểm F sao cho \[CF = BD\]. Gọi M là giao điểm của DF và BC.

Chứng minh rằng \[\frac{{MD}}{{MF}} = \frac{{AC}}{{AB}}\].

Cho tam giác ABC lấy M, N thuộc hai cạnh AB, AC. Nối B với N, C với M. Qua M kẻ đường thẳng song song với BN cắt AC tại I, qua N kẻ đường thẳng song song với CM cắt AB tại K. Chứng minh IK // BC.

Cho hình thang ABCD (AB // CD). Một đường thẳng song song với hai đáy cắt cạnh bên AD ở I, cắt đường chéo BD tại K, AC tại L và cắt cạnh bên BC tại G. Đường thẳng đi qua giao điểm O của hai đường chéo và song song với hai đáy cắt hai cạnh bên ở E và F. Chứng minh OE = OF.