Trắc nghiệm Toán 10 (có đáp án): Một số bài toán về hàm số bậc hai

Cho đồ thị hàm số y = a $$ x 2 + bx + c như hình vẽ.

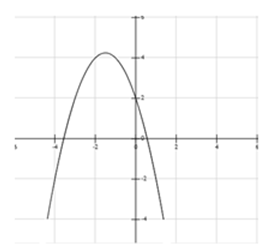
Khẳng định nào sau đây là đúng:

Đồ thị hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

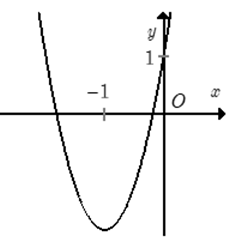
Đồ thị hình vẽ là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

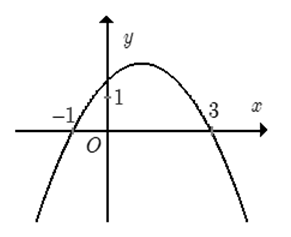
Xác định Parabol (P): y = a $$ x 2 + bx + 2 biết rằng Parabol đi qua hai điểm M (1; 5) và N (2; −2).

Xác định parabol (P): y = a $$ x 2 + bx + 2, biết rằng (P) đi qua hai điểm M (1; 5) và N (−2; 8).

Xác định Parabol (P):  $$ y = ax 2 + b x − 5  biết rằng Parabol đi qua điểm A (3; -4)và có trục đối xứng x =  $$ - 3 2  

Xác định parabol (P): y = 2 $$ x 2 + bx + c, biết rằng (P) đi qua điểm M(0;4) và có trục đối xứng x = 1.

Xác định Parabol (P):  $$ y = ax 2 + bx + 3  biết rằng Parabol có đỉnh I (3; -2)

Tìm parabol (P): y = a $$ x 2 + 3x − 2, biết rằng parabol có đỉnh  $$ I ( − 1 2 ; − 11 4 )  

Viết phương trình của Parabol (P) biết rằng (P) đi qua các điểm A (0; 2), B (-2; 5), C (3; 8)

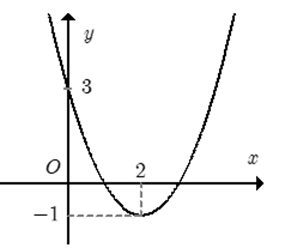
Xác định parabol (P): y = a $$ x 2 + bx + c, biết rằng (P) cắt trục Ox tại hai điểm có hoành độ lần lượt là −1 và 2, cắt trục Oy tại điểm có tung độ bằng −2.

Tìm các giá trị của tham số m để phương trình  $$ 2 x 2 − 2 x + 1 − m = 0 có hai nghiệm phân biệt

Tìm tất cả các giá trị thực của m để phương trình −2 $$ x 2 − 4x + 3 = m có nghiệm.

Tìm các giá trị thực của tham số m để phương trình | $$ x 2 − 3x + 2| = m có bốn nghiệm thực phân biệt.

Cho hàm số f(x) = a $$ x 2 + bx + c đồ thị như hình. Hỏi với những giá trị nào của tham số thực m thì phương trình |f(x)| = m có đúng 4 nghiệm phân biệt.

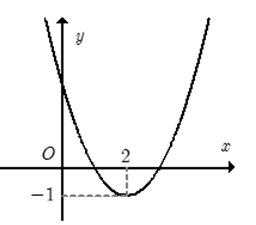
Tìm các giá trị của tham số m để phương trình  $$ 1 2 x 2 − 4 x + 3 = m 2  có 3 nghiệm phân biệt

Cho hàm số f(x) = a $$ x 2 + bx + c đồ thị như hình. Hỏi với những giá trị nào của tham số thực mm thì phương trình f(|x|) – 1 = m có đúng 3 nghiệm phân biệt.

Tìm các giá trị của m để phương trình  $$ x 2 − 2 x + 4 x 2 − 12 x + 9 = m có nghiệm duy nhất

Cho  phương trình của (P): y = a $$ x 2 + bx + c (a $$ ≠   0) biết rằng hàm số  có giá trị lớn nhất bằng 1 và đồ thị hàm số đi qua các điểm A (2; 0), B (−2; −8). Tình tổng  $$ a 2 + b 2 + c 2

Biết rằng hàm số y = a $$ x 2 + bx + c (a $$ ≠ 0) đạt giá trị lớn nhất bằng 3 tại x = 2 và có đồ thị hàm số đi qua điểm A (0; −1). Tính tổng S = a + b + c.

Biết rằng hàm số y = a $$ x 2 + bx + c (a $$ ≠   0) đạt giá trị lớn nhất bằng 5 tại x = − 2 và có đồ thị đi qua điểm M (1; −1). Tính tổng S = $$ a 2 + b 2 + c 2

Biết đồ thị hàm số (P): y = $$ x 2 − ( $$ m 2 + 1)x − 1 cắt trục hoành tại hai điểm phân biệt có hoành độ $$ x 1 ;   x 2 . Tìm giá trị của tham số mm  để biểu thức  $$ T   =   x 1 +   x 2 đạt giá trị nhỏ nhất.

Cho parabol (P): y = $$ x 2 − 4x + 3 và đường thẳng d: y = mx + 3. Tìm tất cả các giá trị thực của mm để d cắt (P) tại hai điểm phân biệt A, B sao cho diện tích tam giác OAB bằng  $$ 9 2 .

Cho parabol (P): y = $$ x 2 − 4x + 3 và đường thẳng d: y = mx + 3. Tìm giá trị thực của tham số m để d cắt (P) tại hai điểm phân biệt A, B có hoành độ $$ x 1 ,   x 2 thỏa mãn  $$ x 1 3 + x 2 3 = 8  

Tìm các giá trị của tham số m để phương trình $$ x 2 − 2(m + 1)x + 1 = 0 có hai nghiệm phân biệt trong đó có đúng một nghiệm thuộc khoảng (0; 1).

Tìm tất cả các giá trị thực của tham số m để phương trình  $$ x 2 − 5 x + 7 + 2 m = 0 có nghiệm thuộc đoạn [1;5]   

Tìm các giá trị của tham số m để  $$ 2 x 2 − 2 ( m + 1 ) x + m 2 − 2 m + 4 ≥ 0    ( ∀ x )  

Tìm giá trị nhỏ nhất của hàm số $$ f ( x ) biết rằng  $$ f ( x + 2 ) = x 2 − 3 x + 2

Cho hàm số f(x) = $$ x 2 + 2x − 3

Xét các mệnh đề sau:

i) f(x − 1) = $$ x 2 − 4

ii) Hàm số đã cho đồng biến trên (−1; + $$ ∞ )

iii) Giá trị nhỏ nhất của hàm số là một số âm.

iv) Phương trình f(x) = m có nghiệm khi m $$ ≥ −4

Số mệnh đề đúng là:

Tìm các giá trị của m để hàm số y = $$ x 2 + mx + 5 luôn đồng biến trên (1; + $$ ∞ )

Tìm giá trị của m để hàm số y = − $$ x 2 + 2x + m − 5 đạt giá trị lớn nhất bằng 6

Biết rằng hàm số y = a $$ x 2 + bx + c (a $$ ≠ 0) đạt giá trị nhỏ nhất bằng 4 tại x = 2 và có đồ thị hàm số đi qua điểm A (0; 6). Tính tích P = abc.

Tìm tất cả các giá trị thực của tham số b để đồ thị hàm số  $$ y = − 3 x 2 + bx − 3 cắt trục hoành tại hai điểm phân biệt

Tìm điểm A cố định mà họ đồ thị hàm số y = $$ x 2 + (2 − m)x + 3m( $$ P m ) luôn đi qua.

Tìm giá trị nhỏ nhất của biểu thức  $$ P = 3 a 2 b 2 + b 2 a 2 − 8 a b + b a