Một khúc gỗ có dạng khối nón có bán kính đáy
r = 30 \text{cm} chiều cao
h = 120 \text{cm}. Anh thợ mộc chế tác khúc gỗ đó thành một khúc gỗ có dạng khối trụ như hình vẽ sau:
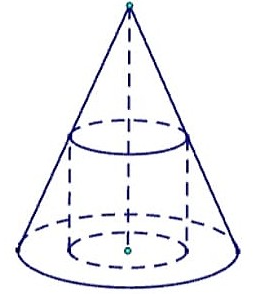
Gọi
là thể tích lớn nhất của khúc gỗ dạng khối trụ có thể chế tác được. Tính
.
A.
.
B.
.
C.
.
D.
.
Đáp án đúng là: C
Một khúc gỗ có dạng khối nón có bán kính đáy
r = 30 \text{cm} chiều cao
h = 120 \text{cm}. Anh thợ mộc chế tác khúc gỗ đó thành một khúc gỗ có dạng khối trụ như hình vẽ sau:

Gọi là thể tích lớn nhất của khúc gỗ dạng khối trụ có thể chế tác được. Tính .
.
.
.
.
Đáp án đúng là: C
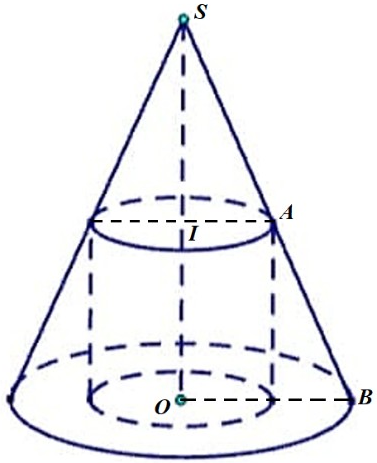
⬩ Xét hình nón với các đỉnh như hình vẽ. Khi đó, .
Đặt . Ta có: .
Suy ra .
⬩ Khi đó, thể tích khối trụ là:
⬩ Vậy thể tích khối trụ lớn nhất là:
Dấu xảy ra khi
Câu hỏi tương tự:
#8273 THPT Quốc giaToán
Một khúc gỗ có dạng khối nón có bán kính đáy
chiều cao
Anh thợ mộc chế tác khúc gỗ đó thành một khúc gỗ có dạng khối trụ như hình vẽ sau:
Gọi là thể tích lớn nhất của khúc gỗ dạng khối trụ có thể chế tác được. Tính
Lượt xem: 140,731 Cập nhật lúc: 12:40 14/05/2025
#8311 THPT Quốc giaToán
Một khúc gỗ có dạng hình khối nón có bán kính đáy
, chiều cao
. Bác thợ mộc chế tác từ gỗ đó thành một khúc gỗ có dạng hình khối trụ như hình vẽ. Gọi
là thể tích lớn nhất của khúc gỗ hình trụ sau khi chế tác. Tính
.
Lượt xem: 141,468 Cập nhật lúc: 21:15 13/05/2025
#6509 THPT Quốc giaVật lý
Trong một thí nghiệm về sự khúc xạ ánh sáng, một học sinh ghi lại trên tấm bia ba đường truyền của ánh sáng như hình vẽ, nhưng quên ghi chiều truyền. (Các) tia nào kể sau có thể là tia phản xạ?
Lượt xem: 110,804 Cập nhật lúc: 20:40 14/05/2025
#7748 THPT Quốc giaToán
Một vật trang trí có dạng khối tròn xoay tạo thành khi quay miền
được giới hạn bởi đường gấp khúc
và cung tròn
(phần gạch chéo trong hình bên) xung quanh trục
. Biết
là hình chữ nhật cạnh
là trung điểm của
; điểm
cách
một đoạn bằng
. Tính thể tích của vật trang trí đó, làm tròn kết quả đến hàng phần mười.
Lượt xem: 131,873 Cập nhật lúc: 20:06 14/05/2025
#6969 THPT Quốc giaVật lý
Một tia sáng đi thủy tinh có chiết suất ra không khí với góc tới là . Góc khúc xạ là
Lượt xem: 118,621 Cập nhật lúc: 21:09 14/05/2025
#2057 THPT Quốc giaVật lý
Chiếu một tia sáng từ không khí vào một môi trường có chiết suất thì tia khúc xạ và phản xạ vuông góc với nhau. Giá trị của góc tới là
Lượt xem: 35,123 Cập nhật lúc: 19:39 13/05/2025
#455 THPT Quốc giaVật lý
Vật kính và thị kính của một kính thiên văn khúc xạ có tiêu cự lần lượt là và . Số bội giác của kính này khi ngắm chừng ở vô cực là
Lượt xem: 7,812 Cập nhật lúc: 21:49 13/05/2025
#1168 THPT Quốc giaVật lý
Xét một tia sáng đơn sắc truyền từ môi trường chiết suất n1 với góc tới sang môi trường chiết suất với góc khúc xạ . Biểu thức liên hệ nào sau đây là đúng?
Lượt xem: 19,996 Cập nhật lúc: 09:12 17/05/2025
#390 THPT Quốc giaVật lý
Chiếu một tia sáng đơn sắc qua mặt phân cách từ môi trường chiết suất n1 sang môi trường chiết suất n2 với góc tới i, gọi r là góc khúc xạ. Công thức liên hệ giữa i và r là
Lượt xem: 6,767 Cập nhật lúc: 09:24 17/05/2025
Đề thi chứa câu hỏi này:
1 mã đề 50 câu hỏi 1 giờ 30 phút
4,218 xem312 thi
