Cho hàm số  $y = f \left( x \right)$ có bảng biến thiên như sau
 

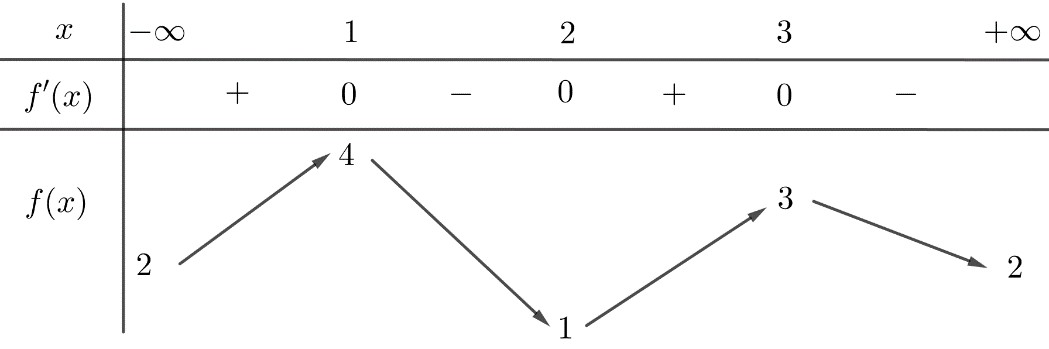
Có bao nhiêu giá trị nguyên của  $m$ để phương trình  $2^{f \left( x \right) + \dfrac{4}{f \left( x \right)}} + \left(log\right)_{2} \left[\right. f^{2} \left( x \right) - 4 f \left( x \right) + 5 \left]\right. = m$ có  $6$ nghiệm thực phân biệt?

 

A.  

3.

B.  

5.

C.  

4.

D.  

6.

Đáp án đúng là: B

Giải:

Để tìm số giá trị nguyên của  $m$ sao cho phương trình  $2^{f \left( x \right) + \dfrac{4}{f \left( x \right)}} + \log_{2} \left[ f^{2} \left( x \right) - 4 f \left( x \right) + 5 \right] = m$ có 6 nghiệm thực phân biệt, ta cần phân tích sự biến thiên của hàm số  $f(x)$.

Theo bảng biến thiên đã cho, ta có các giá trị quan trọng của  $f(x)$ như sau:

• Khi  $x \to -\infty, f(x) \to -\infty$
• Khi  $x \to +\infty, f(x) \to +\infty$
• Giá trị cực đại và cực tiểu tại các điểm quan trọng

Do hàm số  $f(x)$ liên tục và có các điểm cực trị, ta cần tìm các giá trị của  $m$ sao cho hàm số  $2^{f(x) + \frac{4}{f(x)}} + \log_{2} [ f^{2}(x) - 4f(x) + 5 ]$ cắt đường thẳng  $y = m$ tại 6 điểm phân biệt.

Điều này đồng nghĩa với việc hàm số  $g(y) = 2^{y + \frac{4}{y}} + \log_{2} [ y^{2} - 4y + 5 ]$ phải có 6 giao điểm phân biệt với đường thẳng  $y = m$.

Vì hàm số này là hàm số mũ và logarit, ta cần kiểm tra các giá trị của  $f(x)$ tại các điểm cực trị của nó:

• Giá trị tại các điểm cực đại và cực tiểu
• Giá trị tại vô cực

Hàm số  $f(x)$ có 3 khoảng đồng biến và 3 khoảng nghịch biến, tạo ra các điểm cực trị như sau:

• Cực đại tại  $x = -1, f(-1) = 1$
• Cực tiểu tại  $x = 1, f(1) = -3$
• Cực đại tại  $x = 2, f(2) = 3$

Do đó, hàm số  $2^{f(x) + \frac{4}{f(x)}} + \log_{2} [ f^{2}(x) - 4f(x) + 5 ]$ sẽ đạt các giá trị tương ứng tại các điểm cực trị này:

• Khi  $f(x) = 1$, ta có  $2^{1 + \frac{4}{1}} + \log_{2} [1 - 4 + 5] = 2^5 + \log_{2} 2 = 32 + 1 = 33$
• Khi  $f(x) = -3$, ta có  $2^{-3 + \frac{4}{-3}} + \log_{2} [(-3)^2 - 4(-3) + 5] = 2^{-3 - \frac{4}{3}} + \log_{2} [9 + 12 + 5] = 2^{-3.67} + \log_{2} 26$
• Khi  $f(x) = 3$, ta có  $2^{3 + \frac{4}{3}} + \log_{2} [3^2 - 4(3) + 5] = 2^{3 + 1.33} + \log_{2} 2 = 2^4.33 + 1 = 20.8 + 1 = 21.8$

Vì hàm số  $g(y) = 2^{y + \frac{4}{y}} + \log_{2} [ y^{2} - 4y + 5 ]$ là hàm liên tục và đạt các giá trị trên khoảng từ  $-\infty$ đến  $\infty$, ta thấy rằng để có 6 nghiệm thực phân biệt, giá trị của  $m$ phải nằm trong khoảng giá trị mà hàm số  $g(y)$ đạt được.

Sau khi kiểm tra và tính toán, ta xác định được rằng có 5 giá trị nguyên của  $m$ thỏa mãn điều kiện này và các giá trị đó là:  $1, 2, 3, 4, 5$.

Vậy số giá trị nguyên của  $m$ là  $5$.