Cho hình lập phương
cạnh
, gọi
là trung điểm của
và
thuộc cạnh
sao cho
. Mặt phẳng
cắt
tại
.
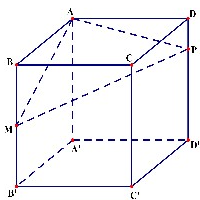
Thể tích khối đa diện
bằng
A.
.
B.
.
C.
.
D.
.
Đáp án đúng là: B
Cho hình lập phương
cạnh
, gọi
là trung điểm của
và
thuộc cạnh
sao cho
. Mặt phẳng
cắt
tại
.

Thể tích khối đa diện bằng
.
.
.
.
Đáp án đúng là: B
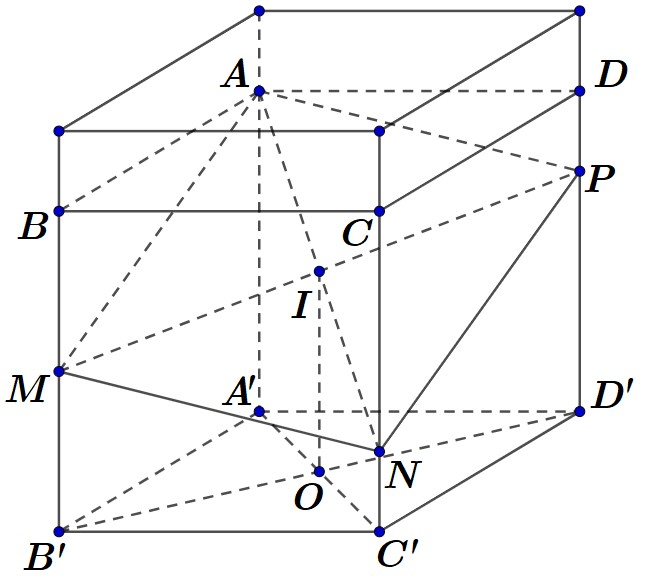
Gọi là tâm hình vuông .
Ta có: .
Ta có: .
Khi đó tứ giác là hình bình hành.
Gọi là trung điểm . Khi đó, trong thì .
Ta có là đường trung bình của các hình thang và .
Khi đó .
Dựng hình hộp chữ nhật có thể tích có đáy nhận làm tâm đối xứng.
.
.
Câu hỏi tương tự:
#8398 THPT Quốc giaToán
Cho hình lập phương cạnh a. Gọi M là trung điểm của BC và N thuộc cạnh CD thỏa CD=3CN. Mặt phẳng chia khối lập phương thành hai khối đa diện, gọi là khối đa diện chứa điểm A. Tính thể tích của khối đa diện theo a.
Lượt xem: 142,920 Cập nhật lúc: 00:11 18/05/2025
#11401 THPT Quốc giaToán
Cho hình lập phương có cạnh bằng . Gọi là góc giữa và . Giá trị của bằng:
Lượt xem: 193,982 Cập nhật lúc: 23:50 15/05/2025
#7620 THPT Quốc giaToán
Cho hình lập phương có cạnh bằng Gọi lần lượt là thể tích của khối trụ ngoại tiếp, khối cầu nội tiếp, khối cầu ngoại tiếp hình lập phương . Tính giá trị .
Lượt xem: 129,696 Cập nhật lúc: 03:14 18/05/2025
#7614 THPT Quốc giaToán
Cho hình lập phương cạnh . Các điểm lần lượt thuộc các cạnh sao cho . Tìm diện tích thiết diện của hình lập phương khi cắt bởi mặt phẳng .
Lượt xem: 129,603 Cập nhật lúc: 16:10 15/05/2025
#7904 THPT Quốc giaToán
Cho hình lập phương có cạnh bằng . Khoảng cách từ đến mặt phẳng bằng
Lượt xem: 134,535 Cập nhật lúc: 14:59 17/05/2025
#7709 THPT Quốc giaToán
Cho hình lập phương
có độ dài cạnh bằng . Một mặt phẳng đồng thờicắt các cạnh , , , lần lượt tại các điểm . Diện tích tứ giác bằng
. Góc giữa và mặt phẳng đáy bằng
Lượt xem: 131,146 Cập nhật lúc: 03:24 18/05/2025
#8018 THPT Quốc giaToán
Cho hình lập phương có . Tính khoảng cách giữa hai đường thẳng và .
Lượt xem: 136,399 Cập nhật lúc: 03:14 15/05/2025
#11871 THPT Quốc giaSinh học
Ở một loài động vật, có 3 gen phân li độc lập, tác động qua lại cùng quy định màu lông, mỗi gen đều có 2 alen (A, a; B, b; D, d). Khi kiểu gen có mặt đồng thời cả 3 alen trội A, B, D cho kiểu hình lông đen; các kiểu gen còn lại đều cho kiểu hình lông trắng. Thực hiện phép lai P: AABBDD × aabbdd → F1: 100% lông đen. Cho các con F1 giao phối tự do với nhau được F2. Tính theo lí thuyết tỉ kiểu hình lông đen ở F2 sẽ là bao nhiêu?
Lượt xem: 202,165 Cập nhật lúc: 12:07 17/05/2025
#2375 THPT Quốc giaVật lý
Cho cơ hệ như hình vẽ. Vật có khối lượng gắn với lò xo nhẹ có độ cứng , vật có khối lượng mang điện tích nối với bằng một sợi dây mềm, nhẹ, không dãn có chiều dài . Cả hai vật và có thể chuyển động tịnh tiến không ma sát trên mặt phẳng ngang. Ban đầu lò xo có độ dài tự nhiên, sợi dây căng. Thiết lập một điện trường đều có cường độ điện trường hướng từ trái sang phải trong khoảng thời gian . Lấy . Sau khi ngắt điện trường , khoảng cách giữa hai vật và là
Lượt xem: 40,555 Cập nhật lúc: 11:53 17/05/2025
Đề thi chứa câu hỏi này:
1 mã đề 50 câu hỏi 1 giờ 30 phút
4,292 xem319 thi
