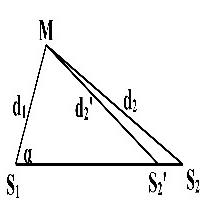
Hai nguồn phát sóng kết hợp S₁, S₂ trên mặt nước cách nhau 10 cm dao động theo phương trình $u_{1} = u_{2} = 2cos \left( 40 \pi t \right)$cm. Xét điểm M trên mặt nước cách S₁, S₂ những đoạn tương ứng là d₁ = 4,2 cm và d₂ = 9 cm. Coi biên độ sóng không đổi và tốc độ truyền sóng trên mặt nước là v = 32 cm/s. Giữ nguyên tần số f và các vị trí S₁, M. Muốn điểm M nằm trên đường cực tiểu giao thoa thì phải dịch chuyển nguồn S₂ dọc theo phương S₁S₂ chiều lại gần S₁ từ vị trí ban đầu một khoảng nhỏ nhất bằng

A.  

0,6 cm.

B.  

0,89 cm.

C.  

0,36 cm.

D.  

0,42 cm.

Đáp án đúng là: B

Hai nguồn sóng kết hợp trên mặt nước cách nhau một đoạn $S_1{S}_2=9\lambda$ phát ra dao động $u=\mathrm{c}\mathrm{o}\mathrm{s}\left(\omega t\right)$. Trên đoạn $S_1{S}_2$, số điểm có biên độ cực đại cùng pha với nhau và ngược pha với nguồn (không kể hai nguồn) là:

Ở mặt chất lỏng, tại hai điểm $S_1$ và $S_2$ cách nhau $25\mathrm{c}\mathrm{m}$ có hai nguồn dao động cùng pha theo phương thẳng đứng phát ra hai sóng kết hợp. Gọi ${\mathrm{\Delta }}_1$ và ${\mathrm{\Delta }}_2$ là hai đường thẳng ở mặt chất lỏng cùng vuông góc với đoạn thẳng $S_1{S}_2$ và cách nhau $12\mathrm{c}\mathrm{m}$. Biết số điểm cực đại giao thoa trên ${\mathrm{\Delta }}_1$ và ${\mathrm{\Delta }}_2$ tương ứng là 9 và 5. Số điểm cực tiểu giao thoa trên đoạn thẳng $S_1{S}_2$ là