Trong một thí nghiệm về giao thoa sóng nước, hai nguồn sóng kết hợp O 1 và O 2 dao động cùng pha, cùng biên độ. Chọn hệ tọa độ vuông góc xOy (thuộc mặt nước) với gốc tọa độ và vị trí đặt nguồn O 1 còn nguồn O 2 nằm trên trục Oy . Hai điểm P và Q nằm trên Ox có OP=4,5 cm và OQ=8 m . Dịch chuyển nguồn O 2 trên trục Oy đến vị trí sao cho góc P O 2 Q có giá trị lớn nhất thì phần tử nước tại P không dao động còn phần tử nước tại Q dao động với biên độ cực đại. Biết giữa P và Q không còn cực đại nào khác. Trên đoạn OP , điểm gần P nhất mà các phần tử nước dao động với biên độ cực đại cách P một đoạn gần nhất với giá trị nào sau đây?
A.
$2,5 c m$
B.
$7,5 c m$
C.
$6,2 c m$
D.
$2,1 c m$
Đáp án đúng là: D

$tan P O_{2} Q = tan \left( Q O_{2} O - P O_{2} O \right) = \dfrac{tan Q O_{2} O - tan P O_{2} O}{1 + tan Q O_{2} O tan P O_{2} O} = \dfrac{\dfrac{8}{O O_{2}} - \dfrac{4 , 5}{O O_{2}}}{1 + \dfrac{8}{O O_{2}} . \dfrac{4 , 5}{O O_{2}}} = \dfrac{3 , 5}{O O_{2} + \dfrac{36}{O O_{2}}} \underset{Cos i}{\leq} \dfrac{3 , 5}{2 \sqrt{36}}$

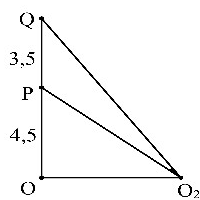
Dấu = xảy ra

\Leftrightarrow O O_{2} = \dfrac{36}{O O_{2}} \Leftrightarrow O O_{2} = 6 c m

$\left{ Q O_{2} - Q O = k \lambda \\ P O_{2} - P O = \left(\right. k + 0 , 5 \right) \lambda \Rightarrow \left{ \sqrt{6^{2} + 8^{2}} - 8 = k \lambda \\ \sqrt{6^{2} + 4 , 5^{2}} - 4 , 5 = \left(\right. k + 0 , 5 \right) \lambda \Rightarrow \left{\right. k = 1 \\ \lambda = 2 c m$
Cực đại gần P nhất có

d_{2} - d_{1} = 2 \lambda \Rightarrow \sqrt{6^{2} + d_{1}^{2}} - d_{1} = 2 . 2 \Rightarrow d_{1} = 2 , 5 c m

Điểm đó cách P là

O P - d_{1} = 4,5 - 2,5 = 2 c m

. Chọn D

Câu hỏi tương tự:

#3706 THPT Quốc giaVật lý

Trong một thí nghiệm về giao thoa sóng trên mặt nước với hai nguồn sóng kết hợp đặt tại A và B dao động điều hòa cùng pha theo phương thẳng đứng cách nhau $A B = 12 c m$ . Biết sóng truyền trên mặt nước có tần số $20 H z$ và tốc độ $50 c m / s$ . Số điểm dao động với biên độ cực đại trên đoạn $A B$ là

Lượt xem: 63,037 Cập nhật lúc: 14:26 19/11/2024

#2936 THPT Quốc giaVật lý

Trong một thí nghiệm về giao thoa sóng nước, hai nguồn A và B cách nhau $16 c m$ , dao động điều hòa theo phương vuông góc với mặt nước với cùng phương trình $u = 2 c o s 16 π t (u$ tính bằng $m m, t$ tính bằng s). Tốc độ truyền sóng trên mặt nước là $12 c m / s$ . Trên đoạn $A B$ , số điểm dao động với biên độ cực đại là

Lượt xem: 49,943 Cập nhật lúc: 17:01 17/11/2024

#4229 THPT Quốc giaVật lý

Trong một thí nghiệm về giao thoa sóng nước, hai nguồn sóng kết hợp dao động cùng pha tại hai điểm A và B trên mặt nước. Sóng do hai nguồn kết hợp có bước sóng là $2,5 c m$ và biên độ lần lượt là $3 c m$ và $2 c m$ . Điểm M trên mặt nước cách $A 25 c m$ và cách $B 30 c m$ sẽ dao động với biên độ là

Lượt xem: 71,925 Cập nhật lúc: 02:40 19/11/2024

#190 THPT Quốc giaVật lý

Trong một thí nghiệm về giao thoa sóng nước, hai nguồn sóng kết hợp được đặt tại A và $B$ dao động theo phương trình $u_{A} = u_{B} = a c o s 30 π t$ ( $a$ không đổi, $t$ tính bằng $s$ ). Tốc độ truyền sóng trong nước là $60 c m / s$ . Hai điểm $P, Q$ nằm trên mặt nước có hiệu khoảng cách đến hai nguồn là $P A - P B = 6 c m, Q A - Q B = 12 c m$ . Kết luận về dao động của $P, Q$ là

Lượt xem: 3,259 Cập nhật lúc: 02:42 19/11/2024

#4600 THPT Quốc giaVật lý

Trong một thí nghiệm về giao thoa sóng nước, hai nguồn sóng kết hợp dao động cùng pha được đặt tại A và B cách nhau $18 c m$ . Sóng truyền trên mặt nước với bước sóng $35 m m$ . Trên đoạn $A B$ , số điểm mà tại đó phần từ nước dao động với biên độ cực đại là

Lượt xem: 78,250 Cập nhật lúc: 13:24 20/11/2024

#3551 THPT Quốc giaVật lý

Trong một thí nghiệm về giao thoa sóng nước, hai nguồn sóng kết hợp được đặt tại $A$ và $B$ dao động theo phương trình $u_{A} = u_{B} = a c o s 25 π t (c m)$ (a không đổi, $t$ tính bằng $s$ ). Trên đoạn thẳng $A B$ , hai điểm có phần tử nước dao động với biên độ cực đại cách nhau một khoảng ngắn nhất $2 c m$ . Tốc độ truyền sóng là

Lượt xem: 60,430 Cập nhật lúc: 01:31 21/11/2024

#1023 THPT Quốc giaVật lý

Trong một thí nghiệm về giao thoa sóng nước, hai nguồn sóng kết hợp được đặt tại $A$ và $B$ dao động theo phương trình $u_{A} = u_{B} = a c o s 25 π t$ ( $a$ không đổi, $t$ tính bằng s). Trên đoạn thẳng $A B$ , hai điểm có phần tử nước dao động với biên độ cực đại cách nhau một khoảng ngắn nhất là $2 c m$ . Tốc độ truyền sóng là

Lượt xem: 17,447 Cập nhật lúc: 13:32 21/11/2024

#6397 THPT Quốc giaVật lý

Trong một thí nghiệm về giao thoa sóng trên mặt nước, hai nguồn kết hợp $A, B$ dao động cùng pha, cùng tần số $f = 20 H z$ . Tại một điểm M trên mặt nước cách các nguồn $A, B$ những khoảng $d_{1} = 25 c m, d_{2} = 20,5 c m$ , sóng có biên độ cực đại. Giữa M và đường trung trực $A B$ có 2 dãy cực đại khác. Tốc độ truyền sóng trên mặt nước là

Lượt xem: 108,820 Cập nhật lúc: 22:28 19/11/2024

#3718 THPT Quốc giaVật lý

Trong một thí nghiệm về giao thoa sóng trên mặt nước, hai nguồn A và B cách nhau $16 c m$ , dao động điều hòa theo phương vuông góc với mặt nước với cùng phương trình $u_{A} = u_{B} = 5 c o s (25 π t) (m m)$ . Tốc độ truyền sóng trên mặt nước là $50 c m / s$ . Gọi O là trung điểm $A B$ , điểm M ở mặt chất lỏng nằm trên đường trung trực của $A B$ và cách O một đoạn $O M = 6 c m$ . Coi biên độ của sóng không đổi khi truyền đi. Khi phần tử chất lỏng tại O có li độ $10 m m$ thì phần tử nước tại M có li độ

Lượt xem: 63,247 Cập nhật lúc: 03:03 20/11/2024

Đề thi chứa câu hỏi này:

82. Đề thi thử TN THPT VẬT LÝ 2024 - Liên trường Yên Thành - Nghệ An. (Có lời giải chi tiết)THPT Quốc giaVật lý

1 mã đề 40 câu hỏi 40 phút

5,880 lượt xem 3,122 lượt làm bài

LetQA - Nền tảng trắc nghiệm & đề thi đa lĩnh vực

Về chúng tôi

LetQA là công cụ hỗ trợ học sinh, sinh viên, giáo viên, tổ chức trong việc ôn luyện, kiểm tra kiến thức; được cung cấp miễn phí cho tất cả người dùng.
LetQA không cung cấp dịch vụ mạng xã hội, không cung cấp thông tin tổng hợp và không thu phí người dùng.

Thông tin liên hệ & hỗ trợ

Email: hotro@letqa.com

Facebook: Let QA (fb.com/letqavn)

Liên kết phổ biến

Danh sách đề thi

Tuyển tập/bộ đề thi

Kho kiến thức

Yêu cầu bổ sung đề thi

Đóng góp đề thi

Website liên kết

Phần mềm kiểm tra trùng lặp Kiểm Tra Tài Liệu

Phần mềm xuất bản tạp chí điện tử VOJS

Công cụ kiểm tra chính tả và thể thức Viver

Công cụ hỗ trợ trích dẫn và phân tích khoa học Scholar Hub

Copyright © 2024 LetQA - Metis,. Jsc. All rights reserved