Cho hàm số
có bảng biến thiên như sau:
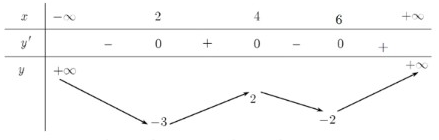
Tổng các giá trị nguyên của tham số
để phương trình
có đúng 8 nghiệm thực phân biệt thuộc khoảng
?
A.
.
B.
.
C.
.
D.
.
Đáp án đúng là: B
Cho hàm số
có bảng biến thiên như sau:

Tổng các giá trị nguyên của tham số để phương trình có đúng 8 nghiệm thực phân biệt thuộc khoảng ?
.
.
.
.
Đáp án đúng là: B
Cho hàm số
có bảng biến thiên như sau:
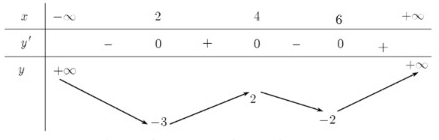
Tổng các giá trị nguyên của tham số để phương trình có đúng 8 nghiệm thực phân biệt thuộc khoảng ?
A. . B. . C. . D. .
Lời giải
Xét hàm số .
Có . Cho .
Ta có:
Bảng biến thiên
|
|
Lại có: .
Ta có: .
Dựa vào bảng biến thiên ta thấy phương trình có tối đa là 5 nghiệm phân biệt
Do đó, để phương trình có đúng 8 nghiệm phân biệt thì
TH1. . Thế vào phương trình (2) ta được . Khi , phương trình (2) có hai nghiệm thỏa yêu cầu.
TH2. .
Với , ta có: (vô lí).
Với , ta có: , .
Vậy có tổng các giá trị nguyên của tham số thỏa yêu cầu đề bài là .
Câu hỏi tương tự:
#8295 THPT Quốc giaToán
Cho hàm số
có bảng biến thiên như sau:
Số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là:
Lượt xem: 141,188 Cập nhật lúc: 11:37 21/05/2025
#8918 THPT Quốc giaToán
Cho hàm số
có bảng biến thiên như sau:
Số đường tiệm cận của đồ thị hàm số đã cho là
Lượt xem: 151,707 Cập nhật lúc: 11:20 21/05/2025
#7740 THPT Quốc giaToán
Cho hàm số
có bảng biến thiên như sau:
Mệnh đề nào dưới đây đúng?
Lượt xem: 131,764 Cập nhật lúc: 07:28 21/05/2025
#8993 THPT Quốc giaToán
Cho hàm số
có bảng biến thiên như sau:
Hàm số đã cho đạt cực đại tại điểm nào dưới đây?
Lượt xem: 153,557 Cập nhật lúc: 07:41 20/05/2025
#8865 THPT Quốc giaToán
Cho hàm số
có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng
Lượt xem: 150,869 Cập nhật lúc: 11:47 21/05/2025
#7889 THPT Quốc giaToán
Cho hàm số
có bảng biến thiên như sau
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Lượt xem: 134,335 Cập nhật lúc: 04:14 22/05/2025
#8972 THPT Quốc giaToán
Cho hàm số
có bảng biến thiên như sau
Mệnh đề nào dưới đây đúng?
Lượt xem: 152,713 Cập nhật lúc: 11:26 21/05/2025
#7832 THPT Quốc giaToán
Cho hàm số
có bảng biến thiên như sau:
Hàm số đồng biến trên khoảng nào dưới đây?
Lượt xem: 133,347 Cập nhật lúc: 13:55 21/05/2025
#8290 THPT Quốc giaToán
Cho hàm số
có bảng biến thiên như sau?
Hàm số đã cho đồng biến trên khoảng nào dưới đây ?
Lượt xem: 141,094 Cập nhật lúc: 11:47 21/05/2025
#8896 THPT Quốc giaToán
Cho hàm số
có bảng biến thiên như sau:
Số điểm cực trị của hàm số bằng
Lượt xem: 151,406 Cập nhật lúc: 11:48 21/05/2025
