
[2021] Trường THPT Chuyên Bắc Ninh lần 3 - Đề thi thử THPT QG năm 2021 môn Toán
Thời gian làm bài: 1 giờ
Đề thi nằm trong bộ sưu tập: 📘 Tuyển Tập Bộ 500 Đề Thi Ôn Luyện Môn Toán THPT Quốc Gia Các Tỉnh Từ Năm 2018-2025 - Có Đáp Án Chi Tiết
Hãy bắt đầu chinh phục nào!
Xem trước nội dung:
Cho giới hạn với là phân số tối giản. Tính giá trị biểu thức
Cho hình chóp có cạnh vuông góc với mặt phẳng biết Tính góc giữa hai mặt phẳng và
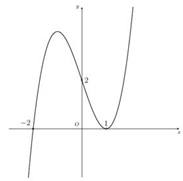
Đường cong trong hình vẽ bên là đồ thị của hàm số nào
Cho hình chóp có đáy là hình vuông cạnh hình chiếu vuông góc của trên mặt phẳng là trung điểm của cạnh Tính theo thể tích khối chóp
Gọi là điểm thuộc đồ thị hàm số Tìm điều kiện của để điểm nằm phía trên đường thẳng
Cho hình chóp S.ABCD đáy là hình vuông tâm cạnh vuông góc với mặt phẳng và Khoảng cách giữa và bằng:
Cho dãy số là cấp số nhân có số hạng đầu công bội Tổng ba số hạng đầu của cấp số nhân là
Cho mặt cầu , mặt phẳng cách tâm một khoảng bằng cắt mặt cầu theo giao tuyến là một đường tròn. Hãy tính theo chu vi của đường tròn là giao tuyến của mặt phẳng và mặt cầu
Đạo hàm của hàm số tại điểm là Tính
Bạn An gửi tiết kiệm một số tiền ban đầu là 1000000 đồng với lãi suất 0,58% / tháng (không kỳ hạn). Hỏi bạn An phải gửi ít nhất bao nhiêu tháng thì được cả vốn lẫn lãi bằng hoặc vượt quá 1300000 đồng?
Thể tích của khối nón có chiều dài đường sinh bằng 3 và bán kính đáy bằng 2 là
Trên giá sách có 6 quyển sách toán khác nhau, 7 quyển sách văn khác nhau và 8 quyển sách Tiếng anh khác. Hỏi có bao nhiêu cách lấy 2 quyển thuộc 2 môn khác nhau?
Cho là hai số thực không âm thỏa mãn Giá trị lớn nhất của là:
Tính tổng tất cả các nghiệm của phương trình trên đoạn
Một hộp có 8 quả cầu đỏ khác nhau, 9 quả cầu trắng khác nhau, 10 quả cầu đen khác nhau. Số cách lấy ngẫu nhiên 1 quả cầu trong hộp là?
Cho dãy số với với . Số 21 là số hạng thứ bao nhiêu của dãy số đã cho?
Nếu dãy số là cấp số cộng có công sai thì ta có công thức là
Giới hạn bằng
Cho số tự nhiên n thỏa mãn Số hạng chứa trong khai triển bằng
Tìm tất cả các giá trị của tham số để đồ thị hàm số có tiệm cận đứng
Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số
Tìm tập hợp tất cả các giá trị của tham số để hàm số có tập xác định là
Thể tích khối cầu có bán kính là:
Hàm số đồng biến trên:
Cho lăng trụ đứng có đáy là tam giác vuông tại Thể tích khối lăng trụ là
Tìm tập nghiệm của phương trình là
Đường cong trong hình bên là đồ thị của hàm số nào trong bốn hàm số dưới đây?
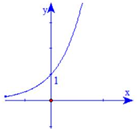
Số nghiệm của phương trình là
Cho hàm số có đạo hàm trên Mệnh đề nào dưới đây là đúng?
Có bao nhiêu cách sắp xếp 8 học sinh thành một hàng dọc
Cho bất phương trình Mệnh đề nào sau đây đúng?
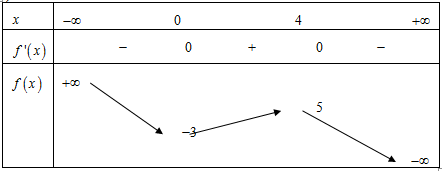
Cho hàm số có bảng biến thiên như sau:
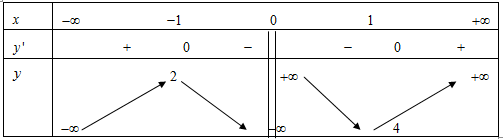
Hàm số nghịch biến trong khoảng nào?
Cho hình chóp tam giác đều có cạnh bên bằng góc giữa cạnh bên và mặt đáy bằng Tính thể tích của khối nón có đỉnh là và đáy là đường tròn ngoại tiếp
Cho hình trụ có bán kính đáy bằng và chiều cao gấp 2 lần đường kính đáy của hình trụ. Tính diện tích xung quanh của hình trụ.
Giới hạn bằng
Có bao nhiêu cách chọn một bạn lớp trưởng và một bạn lớp phó từ một lớp học gồm 35 học sinh, biết rằng em nào cũng có khả năng làm lớp trưởng và lớp phó?
Cho tứ diện đều là trung điểm của Khi đó cosin của góc giữa hai đường thẳng nào sau đây có giá trị bằng
Có bao nhiêu giá trị nguyên của tham số trong để phương trình có nghiệm duy nhất?
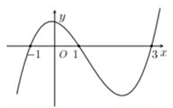
Cho hàm số có đạo hàm liên tục trên Biết hàm số có đồ thị như hình vẽ. Gọi là tập hợp các giá trị nguyên để hàm số nghịch biến trên khoảng Hỏi có bao nhiêu phần tử?
Ông X muốn xây một bình chứa hình trụ có thể tích Đáy làm bằng bê tông giá 100 nghìn đồng/m2, thành làm bằng tôn giá 90 nghìn đồng/m2, nắp bằng nhôm giá 140 nghìn đồng/m2. Vậy đáy của hình trụ có bán kính bằng bao nhiêu để chi phí xây dựng là thấp nhất?
Cho hàm số có đồ thị với là tham số thực. Gọi là điểm thuộc đồ thị có hoành độ bằng 1. Tìm để tiếp tuyến với đồ thị tại cắt đường tròn tạo thành một dây cung có độ dài nhỏ nhất.
Gọi là tập hợp các giá trị nguyên để đồ thị hàm số có 7 điểm cực trị. Tính tổng các phần tử của
Cho hàm số có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm số trên đoạn
Một cơ sở sản xuất có hai bể nước hình trụ có chiều cao bằng nhau, bán kính đáy lần lượt bằng 1m và 1,2m. Chủ cơ sở dự định làm một bể nước mới, hình trụ, có cùng chiều cao và có thể tích bằng tổng thế tích của hai bể nước trên. Bán kính đáy của bể nước dự định làm gần nhất với kết quả nào dưới đây?
Cho hình chóp có đáy hình vuông cạnh Tam giác đều và nằm trong mặt phẳng vuông góc với đáy, bán kính mặt cầu ngoại tiếp hình chóp là:
Cho hình lập phương có tâm Gọi là tâm của hình vuông và là điểm thuộc đoạn thẳng sao cho Khi đó côsin góc tạo bởi hai mặt phẳng và bằng
Cho đa giác lồi Chọn ngẫu nhiên 3 đỉnh của đa giác đó. Xác suất để 3 đỉnh được chọn tạo thành một tam giác không có cạnh nào là cạnh của đa giác đã cho bằng
Gọi là tập hợp tất cả các giá trị thực của tham số để đường thẳng cắt đồ thị hàm số tại 3 điểm phân biệt . B nằm giữa và sao cho Tính tổng các phần tử thuộc
Cho hình chóp có Gọi lần lượt là trọng tâm của các tam giác và đối xứng qua mặt phẳng Thể tích của khối chóp bằng với và tối giản. Tính giá trị
Cho hình lăng trụ có thể tích bằng Gọi lần lượt là trung điểm của các cạnh là điểm trên các cạnh sao cho Thể tích khối tứ diện bằng:
Xem thêm đề thi tương tự

Ôn luyện với đề thi thử THPT Quốc gia môn GDCD năm 2021 từ Trường THPT Chuyên Thái Nguyên. Đề thi bao gồm các câu hỏi trọng tâm về pháp luật, quyền và nghĩa vụ công dân, đạo đức và trách nhiệm xã hội, kèm đáp án chi tiết giúp học sinh lớp 12 củng cố kiến thức và chuẩn bị tốt nhất cho kỳ thi THPT Quốc gia. Đây là tài liệu hữu ích giúp học sinh ôn tập hiệu quả và đạt kết quả cao. Thi thử trực tuyến miễn phí và tiện lợi.
40 câu hỏi 1 mã đề 1 giờ
122,268 lượt xem 65,814 lượt làm bài

Ôn luyện với đề thi thử THPT Quốc gia năm 2021 môn Vật Lý từ Trường THPT Chuyên Nguyễn Bỉnh Khiêm - Quảng Nam. Đề thi bám sát cấu trúc chính thức, bao gồm các câu hỏi trọng tâm về dao động cơ, sóng điện từ, điện xoay chiều, kèm đáp án chi tiết giúp học sinh củng cố kiến thức và chuẩn bị tốt cho kỳ thi tốt nghiệp THPT Quốc gia. Đây là tài liệu hữu ích cho học sinh lớp 12. Thi thử trực tuyến miễn phí và hiệu quả.
40 câu hỏi 1 mã đề 1 giờ
115,656 lượt xem 62,251 lượt làm bài

31 câu hỏi 1 mã đề 1 giờ
196,166 lượt xem 105,623 lượt làm bài

50 câu hỏi 1 mã đề 1 giờ
213,506 lượt xem 114,961 lượt làm bài

40 câu hỏi 1 mã đề 1 giờ
213,968 lượt xem 115,206 lượt làm bài

50 câu hỏi 1 mã đề 1 giờ
194,437 lượt xem 104,692 lượt làm bài

40 câu hỏi 1 mã đề 1 giờ
196,323 lượt xem 105,707 lượt làm bài

40 câu hỏi 1 mã đề 1 giờ
198,374 lượt xem 106,813 lượt làm bài

40 câu hỏi 1 mã đề 1 giờ
208,597 lượt xem 112,315 lượt làm bài
