[2021] Trường THPT Nguyễn Văn Thoại lần 2 - Đề thi thử THPT QG năm 2021 môn Toán

Trong không gian tọa độ Oxyz, đường thẳng $\left( d \right):\frac{x+5}{2}=\frac{y-7}{-8}=\frac{z+13}{9}$ có một véc tơ chỉ phương là

Hình vẽ bên là đồ thị của hàm số nào?

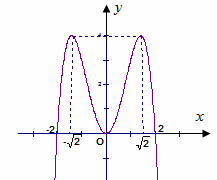
Trong không gian Oxyz, mặt phẳng $\left( \alpha \right):x-y+2z-3=0$ đi qua điểm nào dưới đây?

Với $\alpha$ là một số thực bất kỳ, mệnh đề nào sau đây sai?

Tính diện tích xung quanh $S$ của khối trụ có bán kính đáy $r=4$ và chiều cao $h=3.$

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu $\left( S \right):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-2x+4y-4z-25=0$ . Tìm tọa độ tâm I và bán kính R của mặt cầu $\left( S \right)$ .

Trong không gian Oxyz, hình chiếu vuông góc của điểm $A\left( 3\,;\,2\,;\,-4 \right)$ lên mặt phẳng $\left( Oxy \right)$ có tọa độ là

Cho dãy số $\frac{1}{2};0;-\frac{1}{2};-1;-\frac{3}{2};.....$ là cấp số cộng với

Đạo hàm của hàm số $y={{\pi }^{x}}$ là

Cho tập hợp A gồm có 9 phần tử. Số tập con gồm có 4 phần tử của tập hợp A là

Cho hàm số $y=f\left( x \right)$ có đạo hàm trên $\mathbb{R}$ và có bảng xét dấu ${f}'\left( x \right)$ như sau

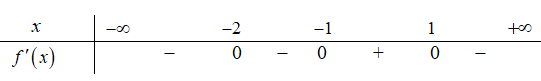
Mệnh đề nào sau đây sai?

Cho đồ thị hàm số $y=f\left( x \right)$ có đồ thị như hình vẽ bên dưới

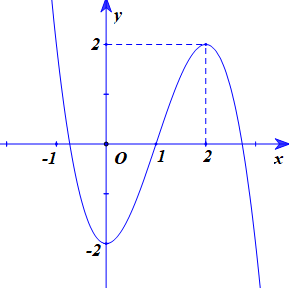
Hàm số $y=f\left( x \right)$ đồng biến trên khoảng nào dưới đây?

Cho hàm $f\left( x \right)$ có đạo hàm liên tục trên $\left[ 2;3 \right]$ đồng thời $f\left( 2 \right)=2,f\left( 3 \right)=5$ . Khi đó $\int\limits_{2}^{3}{{f}'\left( x \right)}\text{d}x$ bằng

Cho số phức $z=-1+2i\,,\,w=2-i$ . Điểm nào trong hình bên biểu diễn số phức z+w?

Cho khối chóp S.ABC có SA, SB, SC đôi một vuông góc và SA=a, SB=b, SC=c. Tính thể tích V của khối chóp đó theo a, b, c.

Cho số phức ${{z}_{1}}=1+i$ và ${{z}_{2}}=2-3i$ . Tìm số phức liên hợp của số phức $\text{w}={{z}_{1}}+{{z}_{2}}$ ?

Cho hàm số $f\left( x \right)={{2}^{x}}+x+1$ . Tìm $\int{f\left( x \right)\text{d}x}$

Đường tiệm cận ngang, đường tiệm cận đứng của đồ thị hàm số $y=\frac{2x-1}{x-2}$ lần lượt có phương trình là

Nghiệm của bất phương trình ${{3}^{x+2}}\ge \frac{1}{9}$ là

Cho hình nón có bán kính đáy $r=\sqrt{3}$ và độ dài đường sinh l=4. Tính diện tích xung quanh ${{S}_{xq}}$ của hình nón đã cho.

Cho tứ diện ABCD có AC=AD và BC=BD. Gọi I là trung điểm của CD. Khẳng định nào sau đây sai?

Biết rằng có duy nhất một cặp số thực $\left( x;\ y \right)$ thỏa mãn $\left( x+y \right)+\left( x-y \right)i=5+3i$ . Tính S=x+2y.

Giá trị lớn nhất của hàm số $f\left( x \right)=\frac{{{x}^{2}}-8x}{x+1}$ trên đoạn $\left[ 1;3 \right]$ bằng

Số nghiệm của phương trình ${{\log }_{2}}\left( {{x}^{2}}\,-\,\,x\,+\,2 \right)=1$ là

Nguyên hàm của hàm số $f\left( x \right)=\sqrt{3x+2}$ là

Trong không gian với hệ tọa độ Oxyz, đường thẳng $\Delta$ đi qua điểm $A\left( -2\,;\,4\,;\,3 \right)$ và vuông góc với mặt phẳng $\left( \alpha \right):\,2x-3y+6z+19=0$ có phương trình là

Cho hàm số $f\left( x \right)$ có đạo hàm ${f}'\left( x \right)={{x}^{3}}\left( x-1 \right)\left( x-2 \right),\,\forall x\in \mathbb{R}.$ Số điểm cực trị của hàm số đã cho là

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB nằm trong mặt phẳng vuông góc với $\left( ABCD \right), \widehat{SAB}={{30}^{0}}, SA=2a$ . Tính thể tích V của khối chóp S.ABCD.

Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, $SA\bot \left( ABCD \right)$ . Gọi I là trung điểm của SC. Khoảng cách từ $I$ đến mặt phẳng $\left( ABCD \right)$ bằng độ dài đoạn thẳng nào?

Với hai số thực dương $a,\,b$ thỏa mãn $\frac{{{\log }_{3}}5{{\log }_{5}}a}{1+{{\log }_{3}}2}-{{\log }_{6}}b=2$ . Khẳng định nào dưới đây là khẳng định đúng?

Bất phương trình ${{4}^{x-15}}<32$ có bao nhiêu nghiệm nguyên dương?

Giá trị của tích phân $I=\int\limits_{0}^{1}{\frac{x}{x+1}}\text{d}x$ là

Hàm số $y=\sqrt{2018x-{{x}^{2}}}$ nghịch biến trên khoảng nào trong các khoảng sau đây?

Tìm số phức z thỏa mãn $\left( 2-3i \right)z-\left( 9-2i \right)=\left( 1+i \right)z.$

Tổ 1 lớp 11A có 6 nam và 7 nữ; tổ 2 có 5 nam và 8 nữ. Chọn ngẫu nhiên mỗi tổ một học sinh. Xác suất để 2 học sinh được chọn đều là nữ là

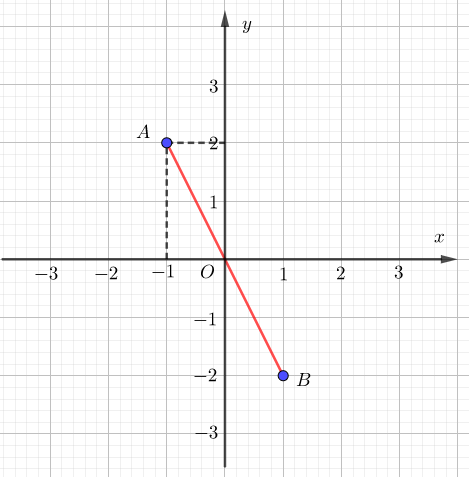
Trong hình vẽ bên, điểm A biểu diễn số phức ${{z}_{1}}$ , điểm B biểu diễn số phức ${{z}_{2}}$ sao cho điểm B đối xứng với điểm A qua gốc tọa độ O. Tìm $\left| z \right|$ biết số phức $z={{z}_{1}}+3{{z}_{2}}$ .

Một đường thẳng cắt đồ thị hàm số $y={{x}^{4}}-2{{x}^{2}}$ tại 4 điểm phân biệt có hoành độ là 0, 1, m và n. Tính $S={{m}^{2}}+{{n}^{2}}$ .

Trong không gian Oxyz, cho hai điểm $A\left( 2\,;\,3\,;\,-5 \right), B\left( -4\,;\,1\,;\,3 \right)$ . Viết phương trình mặt cầu đường kính AB.

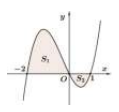
Cho hình phẳng giới hạn bởi đồ thị hàm số $y=f\left( x \right)$ và trục hoành gồm 2 phần, phần nằm phía trên trục hoành có diện tích ${{S}_{1}}=\frac{8}{3}$ và phần nằm phía dưới trục hoành có diện tích ${{S}_{2}}=\frac{5}{12}$ . Tính $I=\int\limits_{-1}^{0}{f\left( 3x+1 \right)\text{d}x}$ .

Trong không gian Oxyz, cho điểm $M(1;\,0;\,1)$ và đường thẳng $d:\frac{x-1}{1}=\frac{y-2}{2}=\frac{z-3}{3}.$ Đường thẳng đi qua M, vuông góc với d và cắt Oz có phương trình là

Cho hàm số y=f(x) có đạo hàm tại $\forall x\in \mathbb{R}$ , hàm số ${f}'(x)={{x}^{3}}+a{{x}^{2}}+bx+c$

Có đồ thị

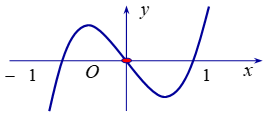
Số điểm cực trị của hàm số $y=f\left[ {f}'\left( x \right) \right]$ là

S là tập tất cả các số nguyên dương của tham số m sao cho bất phương trình ${{4}^{x}}-m{{2}^{x}}-m+15>0$ có nghiệm đúng với mọi $x\in \left[ 1;2 \right]$ . Tính số phần tử của S

Cho hình lăng trụ đứng $ABC.{A}'{B}'{C}'$ có đáy ABC là tam giác đều cạnh bằng a và $\left( {A}'BC \right)$ hợp với mặt đáy ABC một góc $30{}^\circ$ . Tính thể tích V của khối lăng trụ $ABC.{A}'{B}'{C}'$ .

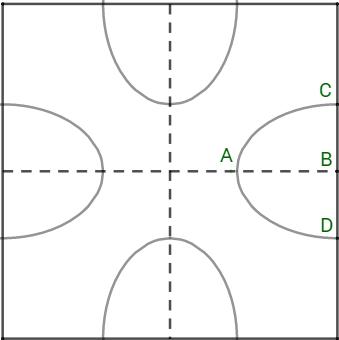
Một hoa văn trang trí được tạo ra từ một miếng bìa mỏng hình vuông cạnh 20cm bằng cách khoét đi bốn phần bằng nhau có hình dạng một nửa elip như hình bên. Biết một nửa trục lớn AB=6cm, trục bé CD=8cm. Diện tích bề mặt hoa văn đó bằng

Trên một cánh đồng có 2 con bò được cột vào 2 cây cọc khác nhau. Biết khoảng cách giữa 2 cọc là 4 mét còn 2 sợi dây cột 2 con bò dài 3 mét và 2 mét. Tính phần diện tích mặt cỏ lớn nhất mà 2 con bò có thể ăn chung.

Cho hàm số $f\left( x \right)$ liên tục trên R và thỏa $\int\limits_{0}^{3}{f\left( \sqrt{{{x}^{2}}+16}+x \right)\text{d}x=2019,}\int\limits_{4}^{8}{\frac{f\left( x \right)}{{{x}^{2}}}\text{d}x=1.}$ Tính $\int\limits_4^8 {f\left( x \right){\rm{d}}x} .$

Cho hàm số $f\left( x \right)=\frac{1}{4}{{x}^{4}}-m{{x}^{3}}+\frac{3}{2}\left( {{m}^{2}}-1 \right){{x}^{2}}+\left( 1-{{m}^{2}} \right)x+2019$ với m là tham số thực. Biết rằng hàm số $y=f\left( \left| x \right| \right)$ có số điểm cực trị lớn hơn 5 khi $a<{{m}^{2}}<b+2\sqrt{c}\,\left( a,\,b,\,c\,\in \mathbb{R} \right)$ . Tích abc bằng

Cho phương trình: ${{2}^{{{x}^{3}}+{{x}^{2}}-2x+m}}-{{2}^{{{x}^{2}}+x}}+{{x}^{3}}-3x+m=0$ . Tập các giá trị để bất phương trình có ba nghiệm phân biệt có dạng $\left( a\,;\,b \right)$ . Tổng a+2b bằng:

Cho số phức z thỏa mãn $\left| z \right|=2$ . Tìm giá trị nhỏ nhất của biểu thức $P=\left| z-4 \right|+2\left| z-3+2i \right|$ .

Trong không gian với hệ tọa độ Oxyz, cho hai mặt cầu $\left( {{S}_{1}} \right),\left( {{S}_{2}} \right)$ lần lượt có phương trình là ${{x}^{2}}+{{y}^{2}}+{{z}^{2}}-2x-2y-2z-22=0, {{x}^{2}}+{{y}^{2}}+{{z}^{2}}-6x+4y+2z+5=0$ . Xét các mặt phẳng $\left( P \right)$ thay đổi nhưng luôn tiếp xúc với cả hai mặt cầu đã cho. Gọi $M\left( a;b;c \right)$ là điểm mà tất cả các $mp\left( P \right)$ đi qua. Tính tổng S=a+b+c.