[2022] Trường THPT Nguyễn Thị Diệu - Đề thi thử THPT QG năm 2022 môn Toán

Cho hàm số $y = {{2x - 3} \over {4 - x}}$ . Trong các mệnh đề sau, mệnh đề nào đúng ?

Cho hàm số $y = x^2$ . Chọn khẳng định sai trong số các khẳng định sau:

Phương trình ${\log _2}^2x - 4{\log _2}x + 3 = 0$ có tập nghiệm là:

Biết ${\log _9}5 = a$ . Khi đó giá trị của ${\log _3}5$ được tính theo a là :

Biến đổi $\int\limits_0^3 {\dfrac{x}{{1 + \sqrt {1 + x} }}\,dx}$ thành $\int\limits_1^2 {f(t)\,dt\,,\,\,t = \sqrt {x + 1} }$ . Khi đó f(t) là hàm nào trong các hàm số sau ?

Tập hợp các điểm biểu diễn thỏa mãn $|z| = |1 + i|$ là :

Cho z = 2i – 1 .Phần thực và phần ảo của $\overline z$ là;

Thể tích khối tứ diện đều có cạnh bằng 1 là:

Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, BC = b, AA′ = c. Gọi M và N theo thứ tự là trung điểm của A'B' và B'C'. Tỉ số giữa thể tích của khối chóp D'.DMN và thể tích khối hộp chữ nhật ABCD.A'B'C'D' là:

Cho hình trụ có bán kính đáy bằng $3{\rm{ cm}}$ , trục $OO' = 8{\rm{ cm}}$ và mặt cầu đường kính $OO'$ . Hiệu số giữa diện tích mặt cầu và diện tích xung quanh hình trụ là

Tung độ của điểm $M$ thỏa mãn $\overrightarrow {OM} = 2\overrightarrow j - \overrightarrow i + \overrightarrow k$ là:

Hàm số $y = {\left( {9{x^2} - 1} \right)^{ - 3}}$ có tập xác định là :

Tính đạo hàm của hàm số $y = \root 3 \of {{x^4} + 1}$ .

Cho hàm số f liên tục trên đoạn [0 ; 6]. Nếu $\int\limits_1^5 {f(x)\,dx = 2\,,\,\,\int\limits_1^3 {f(x)\,dx = 7} }$ thì $\int\limits_3^5 {f(x)\,dx}$ có giá trị bằng bao nhiêu ?

Cho tích phân $I = \int\limits_a^b {f(x).g'(x)\,dx}$ , nếu đặt $\left\{ \begin{array}{l}u = f(x)\\dv = g'(x)\,dx\end{array} \right.$ thì:

Cho hình chóp S.ABCD. Trên các đoạn thẳng SA, SB, SC lần lượt lấy ba điểm A', B', C' khác với S. khi đó tỉ số về thể tích: $\dfrac{{{V_{S.A'B'C;}}}}{{{V_{S.ABC}}}}$ được tính bằng:

Thể tích của khối cầu ngoại tiếp một hình hộp chữ nhật có ba kích thước $a,\,2a,\,2a$ bằng

Điểm $N$ là hình chiếu của $M\left( {x;y;z} \right)$ trên trục tọa độ $Oz$ thì:

Cho mặt cầu bán kính $5{\rm{ cm}}$ và một hình trụ có bán kính đáy bằng $3{\rm{ cm}}$ nội tiếp trong hình cầu. Thể tích của khối trụ là

Giá trị lớn nhất của hàm số $y = {x^3} - 3{x^2} - 9x + 10$ trên [- 2 ; 2] là:

Cho hàm số y = f(x) có bảng biến thiên như sau:

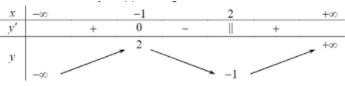
Mệnh đề nào dưới đây là sai ?

Biết $\int\limits_1^4 {f(t)\,dt = 3,\,\,\int\limits_1^2 {f(t)\,dt = 3} }$ . Phát biểu nào sau đây nhân giá trị đúng ?

Tìm nguyên hàm của hàm số $f(x) = {2^{2x}}{.3^x}{.7^x}$ .

Nghịch đảo của số phức z = 1 – 2i là:

Căn bậc hai của số a = - 5 là:

Một mặt cầu có bán kính bằng $10{\rm{ cm}}$ . Một mặt phẳng cách tâm mặt cầu $8{\rm{ cm}}$ cắt mặt cầu theo một đường tròn. Chu vi của đường tròn đó bằng

Gọi $G\left( {4; - 1;3} \right)$ là tọa độ trọng tâm tam giác $ABC$ với $A\left( {0;2; - 1} \right),B\left( { - 1;3;2} \right)$ . Tìm tọa độ điểm $C$ .

Tìm tất cả các giá trị thực của tham số m để hàm số $y = (m + 1){x^4} - m{x^2} + 3$ có ba điểm cực trị.

Hàm số $y = \sqrt {8 + 2x - {x^2}}$ đồng biến trên khoảng nào sau đây ?

Gọi x₁, x₂ là hai nghiệm của phương trình ${\log _2}^2x - 3{\log _2}x + 2 = 0$ . Giá trị biểu thức $P = {x_1}^2 + {x_2}^2$ bằng bao nhiêu ?

Phương trình ${\log _2}({x^2} - 2x + 3) = 1$ có mấy nghiệm ?

Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = \sqrt x - x$ và trục hoành.

Tìm nguyên hàm của hàm số $f(x) = \dfrac{{{{\left( {{x^2} - 1} \right)}^2}}}{{{x^2}}}$ .

Trong các kết luận sau, kết luận nào sai ?

Cho biểu thức $A = i + {i^2} + {i^3} + ... + {i^{99}} + {i^{100}}$ . Giá trị của A là:

Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a. Hình chiếu vuông góc của tam giác SAB xuống mặt phẳng (ABC) có diện tích bằng:

Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a. Gọi I là trung điểm của cạnh SC. Hình chiếu vuông góc của tam giác IAB xuống mặt phẳng (ABC) có diện tích bằng:

Cho tứ diện $ABCD$ có $AD \bot \left( {ABC} \right)$ , $DB \bot BC$ , $AB = AD = BC = a$ . Kí hiệu ${V_1}$ , ${V_2}$ , ${V_3}$ lần lượt là thể tích của hình tròn xoay sinh bởi tam giác $ABD$ khi quay quanh $AD$ , tam giác $ABC$ khi quay quanh $AB$ , tam giác $DBC$ khi quay quanh $BC$ . Trong các mệnh đề sau, mệnh đề nào đúng?

Cho tứ diện $ABCD$ có $A\left( {1;0;0} \right),B\left( {0;1;1} \right),C\left( { - 1;2;0} \right),$$\,D\left( {0;0;3} \right)$ . Tọa độ trọng tâm tứ diện $G$ là:

Số điểm cực trị của hàm số $y = {(x - 1)^{2019}}$ là

Số giao điểm của đường thẳng y= x + 2 và đồ thị hàm số $y = {{3x - 2} \over {x - 1}}$ là

Cho $f(x) = \dfrac{{{e^x}}}{{{x^2}}}$ . Đạo hàm f’(1) bằng :

Rút gọn biểu thức ${b^{{{\left( {\sqrt 3 - 1} \right)}^2}}}:{b^{ - 2\sqrt 3 }}\,\,(b > 0)$ , ta được:

Nguyên hàm của hàm số $f(x) = \dfrac{{\cos 2x}}{{{{\cos }^2}x{{\sin }^2}x}}$ là:

Tính tích phân $\int\limits_{\dfrac{\pi }{4}}^{\dfrac{\pi }{2}} {\cot x\,dx}$ ta được kết quả là :

Cho hai số phức ${z_1} = - 3 + 4i\,,\,\,{z_2} = 4 - 3i$ . Mô đun cảu số phức $z = {z_1} + {z_2} + {z_1}.{z_2}$ là :

Trong mặt phẳng tọa độ với hệ tọa độ Oxy, cho các điểm A (4 ; 0), B(1 ; 4), C(1 ; - 1). Gọi G là trọng tâm của tam giác ABC. Biêt rằng G là điểm biểu diễn số phức z. Mệnh đề nào sau đây đúng ?

Cho các mệnh đề sau:

a. Hình chóp có đáy là hình thang thì có mặt cầu ngoại tiếp.

b. Hình chóp có đáy là hình thang cân thì có mặt cầu ngoại tiếp.

c. Hình chóp có đáy là hình chữ nhật thì có mặt cầu ngoại tiếp.

d. Hình chóp có đáy là hình thoi thì có mặt cầu ngoại tiếp.

Số mệnh đề đúng là?

Cho hai điểm $A$ , $B$ phân biệt. Tập hợp tâm những mặt cầu đi qua $A$ và $B$ là