[2023] Trường THPT Nguyễn Thị Diệu - Đề thi thử THPT QG năm 2023 môn Toán

Số đường tiệm cận của đồ thị hàm số $y=\frac{2x-1}{x+3}$ bằng:

Số phức $z=2-3i$ có số phức liên hợp là:

Giá trị của giới hạn $\underset{x\to 2}{\mathop{\lim }}\,\left( {{x}^{2}}+1 \right)$ là:

Giả sử $F(x)$ là một nguyên hàm của hàm số $f\left( x \right)={{e}^{x}}$ , biết $F\left( 0 \right)=4$ . Tìm $F\left( x \right)$ .

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu $\left( S \right):{{\left( x-1 \right)}^{2}}+{{\left( y+2 \right)}^{2}}+{{\left( z+1 \right)}^{2}}=9$ . Tọa độ tâm I và bán kính R của (S) là:

Tìm nguyên hàm $I=\int{({{e}^{-x}}+2x)dx}$ .

Đồ thị hàm số $y={{x}^{4}}-{{x}^{3}}-3$ cắt trục tung tại mấy điểm

Trong không gian với hệ tọa độ Oxyz, cho điểm $A\left( -3;2;-1 \right)$ . Tọa độ điểm A’ đối xứng với A qua gốc tọa độ O là:

Cho hàm số $y=f(x)$ có bảng biến thiên như sau:

Xác định số điểm cực tiểu của hàm số $y=f\left( x \right)$ .

Có 2 kiểu đồng hồ đeo tay (vuông, tròn) và 3 kiểu dây (kim loại, da, nhựa). Hỏi có bao nhiêu cách chọn một chiếc đồng hồ gồm một mặt và một dây?

Giá trị nhỏ nhất của hàm số $y=4{{x}^{3}}-3{{x}^{4}}$ trên đoạn $\left[ -1;2 \right]$ là:

Trong không gian với hệ tọa độ Oxyz, phương trình nào sau đây là phương trình chính tắc của đường thẳng đi qua hai điểm $A\left( 1;2;-3 \right),\,\,B\left( 7;0;-1 \right)$ ?

Cho chóp đều $S.ABCD$ có cạnh đáy bằng 4, cạnh bên bằng 3. Gọi $\varphi$ là góc giữa cạnh bên và mặt đáy. Khẳng định nào sau đây đúng?

Tìm hệ số của ${{x}^{2}}$ trong khai triển ${{\left( 2x+\frac{1}{{{x}^{2}}} \right)}^{5}}$ .

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, SA vuông góc với đáy. Gọi M là trung điểm AC. Khẳng định nào sau đây sai?

Cho hình lập phương ABCD.A’B’C’D’. Góc giữa A’C’ và D’C là:

Gieo một con xúc xắc cân đối đồng chất. Tính xác suất hiện mặt có số chấm là chẵn.

Cho số phức z thỏa mãn $\overline{z}=\frac{{{\left( 1+\sqrt{3}i \right)}^{3}}}{1+i}$ . Tính mô đun của số phức $\overline{z}-iz$ .

Tính diện tích S hình phẳng giới hạn bởi các đường $y={{x}^{2}}$ và $y=-2x$

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (Q) : $x+2y-3z-15=0$ và điểm $E(1;2;-3)$ . Mặt phẳng (P) qua E và song song với (Q) có phương trình là:

Rút gọn biểu thức $A=\frac{\sqrt[3]{{{a}^{8}}}.{{a}^{\frac{7}{3}}}}{{{a}^{5}}.\sqrt[4]{{{a}^{-3}}}}$ với a>0 ta được kết quả $A={{a}^{\frac{m}{n}}}$ , trong đó $m,n\in {{N}^{*}}$ và $\frac{m}{n}$ là phân số tối giản. Khẳng định nào sau đây đúng?

Nếu {{\left( 2-\sqrt{3} \right)}^{a-1}}<2+\sqrt{3} thì

Cho mặt cầu (S) tâm I bán kính R. Một mặt phẳng cắt mặt cầu (S) và cách tâm I một khoảng bằng $\frac{R}{2}$ . Bán kính của đường tròn do mặt phẳng cắt mặt cầu tạo nên là:

Hàm số $y=\sqrt{{{x}^{2}}-2x}$ nghịch biến trên khoảng nào?

Cho hàm số $y=f(x)$ có bảng biến thiên như sau

Tìm tất cả các giá trị của m để phương trình $f\left( x \right)=m$ có đúng 2 nghiệm.

Cho hàm số $f(x)=\left| {{x}^{3}}-3{{x}^{2}}+m \right|$ với $m\in \left[ -5;7 \right]$ là tham số. Có bao nhiêu giá trị nguyên của m để hàm số $f\left( x \right)$ có đúng 3 điểm cực trị?

Cho một hình trụ có bán kính đáy bằng R và có chiều cao bằng $R\sqrt{3}$ . Hai điểm A, B lần lượt nằm trên hai đường tròn đáy sao cho khoảng cách giữa AB và truc của hình trụ bằng $\frac{R\sqrt{3}}{2}$ . Góc giữa AB và trục của hình trụ bằng:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình ${{x}^{2}}+{{y}^{2}}+{{z}^{2}}-\left( 4m-2 \right)x+2my$$+\left( 4m+2 \right)z-7=0$ . Giá trị nhỏ nhất của thể tích khối cầu là:

Cho $f,\,\,g$ là hai hàm liên tục trên $\left[ 1;3 \right]$ thỏa mãn: $\int\limits_{1}^{3}{\left[ f\left( x \right)+3g\left( x \right) \right]dx=10}$ và $\int\limits_{1}^{3}{\left[ 2f\left( x \right)-g\left( x \right) \right]dx}=6$ . Tính $\int\limits_{1}^{3}{\left[ f\left( x \right)+g\left( x \right) \right]dx}$ .

Cho $f(x)=a.\ln \left( x+\sqrt{{{x}^{2}}+1} \right)+b.{{x}^{2017}}+2018$ với $a,b\in R$ . Biết rằng $f\left( \log \left( \log e \right) \right)=2019$ . Tính giá trị của $f\left( \log \left( \ln 10 \right) \right)$ .

Trong không gian với hệ tọa độ Oxyz, cho điểm $M\left( 1;3;-2 \right)$ . Gọi (P) là mặt phẳng đi qua điểm M và cách gốc tọa độ O một khoảng lớn nhất, mặt phẳng (P) cắt trục Oy tại điểm B. Tọa độ điểm B là:

Cho số phức $z=a+bi,\,\,\left( a,b\in R \right)$ thỏa mãn $\left( 1-3i \right)z+\left( 2+3i \right)\overline{z}=12-i$ . Tính $P={{a}^{2}}-{{b}^{3}}$ .

Cho hàm số $y=f(x)$ có đạo hàm $f'\left( x \right)=2018{{\left( x-1 \right)}^{2017}}{{\left( x-2 \right)}^{2018}}{{\left( x-3 \right)}^{2019}}$ . Tìm số điểm cực trị của $f(x)$ .

Cho dãy số $\left( {{u}_{n}} \right)$ thỏa mãn $\ln \left( {{u}_{3}}-4 \right)=\ln \left( 2{{u}_{n}}-4n+3 \right)$ với mọi $n\in {{N}^{*}}$ . Tính tổng ${{S}_{100}}={{u}_{1}}+{{u}_{2}}+...+{{u}_{100}}$ .

Tìm số thực m>1 thỏa mãn $\int\limits_{1}^{m}{\left( \ln x+1 \right)dx}=m$ .

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng $(P):x+y+z-3=0$ , đường thẳng $d:\frac{x-2}{-1}=\frac{y-8}{1}=\frac{z+1}{-3}$ và điểm $M\left( 1;-1;0 \right)$ . Điểm N thuộc (P) sao cho MN song song d. Độ dài MN là:

Cho hàm số $f\left( x \right)$ có đạo hàm trên đoạn $\left[ a;b \right]$ và $f\left( a \right)=f\left( b \right)$ . Hỏi mệnh đề nào sau đây đúng?

Hàm số $y=\frac{1}{3}{{x}^{3}}-\left( m-3 \right)x+2018$ luôn đồng biến trên R thì:

Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số $y=\frac{x-3}{{{x}^{2}}-2mx+1}$ có 2 đường tiệm cận đứng.

Hàm số $y={{\sin }^{4}}x+{{\cos }^{4}}x$ có tập giá trị $T=\left[ a;b \right]$ . Giá trị $b-a$ là:

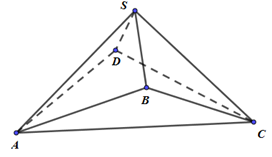
Cho hình đa diện SABCD có $SA=4,\,\,SB=2,\,\,SC=3,\,\,SD=1$ và $\widehat{ASB}=\widehat{BSC}=\widehat{CSD}=\widehat{DSA}={{60}^{0}}$ . Khoảng cách từ điểm A tới mặt phẳng $(SCD)$ là:

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: $\frac{x-13}{-1}=\frac{y+1}{1}=\frac{z}{4}$ và mặt cầu $(S):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-2x-4y-6z-67=0$ . Qua d dựng các mặt phẳng tiếp xúc với (S) lần lượt tại ${{T}_{1}},\,\,{{T}_{2}}$ . Tìm tọa độ trung điểm H của ${{T}_{1}}{{T}_{2}}$ .

Cho hàm số $y=f(x)$ liên tục và có đạo hàm trên R thỏa mãn $f(2)=-2,\,\,\int\limits_{0}^{2}{f\left( x \right)dx}=1$ . Tính tích phân $I=\int\limits_{0}^{4}{f'\left( \sqrt{x} \right)dx}$ .

Cho đa giác đều 60 đỉnh nội tiếp một đường tròn. Số tam giác tù được tạo thành từ 3 trong 60 đinh của đa giác là:

Khối chóp S.ABCD có đáy là hình thoi cạnh a, $SA=SB=SC=a$ , cạnh SD thay đổi. Thể tích khối chóp S.ABCD lớn nhất khi độ dài cạnh SD là:

Cho hàm số $f(x)={{x}^{3}}+a{{x}^{2}}+bx-2$ thỏa mãn $\left\{ \begin{array}{l}a + b &gt; 1\\3 + 2a + b &lt; 0\end{array} \right.$ . Số điểm cực trị của hàm số $y = \left| {f\left( {\left| x \right|} \right)} \right|$ là:

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A. Cạnh AC = a, $BC = a\sqrt 5$ . Mặt phẳng (SAB) vuông góc mặt phẳng đáy và tam giác SAB đều. Gọi K điểm thuộc cạnh SC sao cho SC = 3SK. Tính khoảng cách $d$ giữa hai đường thẳng AC và BK theo a.

Trong mặt phẳng với hệ trục tọa độ $Oxy$ Cho hai đường thẳng ${\Delta _1}$ và ${\Delta _2}$ lần lượt có phương trình: $x - 2y + 1 = 0$ và $x - 2y + 4 = 0$ , điểm $I\left( {2;1} \right).$ Phép vị tự tâm $I$ tỉ số $k$ biến đường thẳng ${\Delta _1}$ thành ${\Delta _2}.$ Tìm $k.$