Trang chủ Đề thi THPT Quốc gia Toán [2021] Bộ GD&ĐT - Mã đề 118 - Đề thi THPT QG năm 2021 môn Toán
thumbnail

[2021] Bộ GD&ĐT - Mã đề 118 - Đề thi THPT QG năm 2021 môn Toán

Đề thi THPT Quốc gia môn Toán năm 2021 - Mã đề 118 được biên soạn và công bố bởi Bộ Giáo dục và Đào tạo. Đề thi tập trung vào các dạng bài quan trọng như hàm số, logarit, hình học không gian, và các câu hỏi tư duy logic. Đề thi có đáp án chi tiết, là tài liệu quan trọng để học sinh lớp 12 ôn luyện và chuẩn bị tốt nhất cho kỳ thi THPT Quốc gia.

Từ khoá: Toán học hàm số logarit hình học không gian tư duy logic năm 2021 Bộ GD&ĐT Mã đề 118 đề thi THPT Quốc gia đề thi có đáp án

Thời gian làm bài: 1 giờ

Đề thi nằm trong bộ sưu tập: 📘 Tuyển Tập Bộ 500 Đề Thi Ôn Luyện Môn Toán THPT Quốc Gia Các Tỉnh Từ Năm 2018-2025 - Có Đáp Án Chi Tiết


Bạn chưa làm đề thi này!!!

Hãy bắt đầu chinh phục nào!



 

Xem trước nội dung:

Câu 1: 1 điểm

Cho hai số phức z = 5 + 2i và w = 1 - 4i. Số phức z + w bằng

A.  
6 + 2i
B.  
-4 - 6i
C.  
6 - 2i
D.  
4 + 6i
Câu 2: 1 điểm

Thể tích của khối lập phương cạnh 4a bằng:

A.  
64 a3{{a}^{3}}
B.  
8 a3{{a}^{3}}
C.  
16 a3{{a}^{3}}
D.  
32 a3{{a}^{3}}
Câu 3: 1 điểm

Trong không gian Oxyz, cho mặt phẳng (P): -2x+5y+z-3=0. Vec tơ nào dưới đây là một vec tơ pháp tuyển của (P)?

A.  
n⃗3=(2;−5;1){{\vec{n}}_{3}}=(2;-5;1)
B.  
n⃗4=(2;5;−1){{\vec{n}}_{4}}=(2;5;-1)
C.  
n⃗1=(2;5;1){{\vec{n}}_{1}}=(2;5;1)
D.  
n⃗2=(−2;5;1){{\vec{n}}_{2}}=(-2;5;1)
Câu 4: 1 điểm

Phần thực của số phức: z = 6-2i bằng:

A.  
2
B.  
-6
C.  
6
D.  
2
Câu 5: 1 điểm

Cho hàm số f(x) = ex + 1. Khẳng định nào dưới đây đúng?

A.  
∫f(x)dx=ex−1+C\int {f(x)dx = {e^{x - 1}}} + C
B.  
∫f(x)dx=ex+C\int {f(x)dx = {e^{x }}} + C
C.  
∫f(x)dx=ex+x+C\int {f(x)dx = {e^{x }}} + x + C
D.  
∫f(x)dx=ex−x+C\int {f(x)dx = {e^{x }}} -x + C
Câu 6: 1 điểm

Cho a > 0 và ae1a e 1 , khi đó loga a3\sqrt[3]{a} bằng

A.  
3
B.  
-3
C.  
−13\frac{-1}3
D.  
13\frac13
Câu 7: 1 điểm

Cho hàm số y = f(x) có bảng biến thiên như sau:

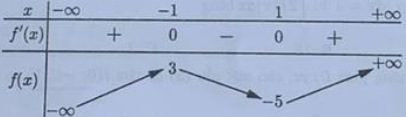
Hình ảnh

Giá trị cực đại của hàm số đã cho bằng

A.  
3
B.  
-1
C.  
-5
D.  
1
Câu 8: 1 điểm

Trên khoảng (0; +∞ + \infty ), đạo hàm của hàm số y=x54y = {x^{\frac{5}{4}}}

A.  
y′=54x14y' = \frac{5}{4}{x^{\frac{1}{4}}}
B.  
y′=54x−14y' = \frac{5}{4}{x^{\frac{-1}{4}}}
C.  
y′=49x94y' = \frac{4}{9}{x^{\frac{9}{4}}}
D.  
y′=45x14y' = \frac{4}{5}{x^{\frac{1}{4}}}
Câu 9: 1 điểm

Trong không gian Oxyz, cho điểm A(4;-1;3). Tọa độ của vecto OA→\overrightarrow {OA} là

A.  
(4;1;3)
B.  
(4;-1;3)
C.  
(-4;1;3)
D.  
(-4;1;-3)
Câu 10: 1 điểm

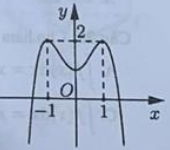
Cho hàm số y = f(x) có đồ thị là đường cong trong hình bên. Hàm số đã cho đồng biến trên khoảng nào sau đây?

Hình ảnh

A.  
(0;1)
B.  
(0; +∞ + \infty )
C.  
(-1;1)
D.  
( −∞ - \infty ;0)
Câu 11: 1 điểm

Cho cấp số nhân (un) với u1 = 3 và u2 = 12. Công bội của cấp số nhân đã cho bằng

A.  
4
B.  
-9
C.  
9
D.  
14\frac{1}{4}
Câu 12: 1 điểm

Nếu ∫14f(x)dx=6\int\limits_{1}^{4}{f(x)dx=6} và ∫14g(x)dx=−5\int\limits_{1}^{4}{g(x)dx=-5} thì ∫14[f(x)−g(x)]dx\int\limits_{1}^{4}{\left[ f(x)-g(x) \right]dx} bằng

A.  
1
B.  
-11
C.  
-1
D.  
11
Câu 13: 1 điểm

Trong không gian Oxyz, cho đường thẳng d đi qua điểm M(2;2;1) và có một vecto chỉ phương u→=(5;2;−3)\overrightarrow{u}=(5;2;-3) . Phương trình của d là:

A.  
{x=5+2ty=2+2tz=−3+t\left\{ \begin{array}{l} x = 5 + 2t\\ y = 2 + 2t\\ z = - 3 + t \end{array} \right.
B.  
{x=2+5ty=2+2tz=1−3t\left\{ \begin{array}{l} x = 2 + 5t\\ y = 2 + 2t\\ z = 1 - 3t \end{array} \right.
C.  
{x=2+5ty=2+2tz=−1−3t\left\{ \begin{array}{l} x = 2 + 5t\\ y = 2 + 2t\\ z = - 1 - 3t \end{array} \right.
D.  
{x=2+5ty=2+2tz=1+3t\left\{ \begin{array}{l} x = 2 + 5t\\ y = 2 + 2t\\ z = 1 + 3t \end{array} \right.
Câu 14: 1 điểm

Tiệm cận đứng của đồ thị hàm số y=x+1x−2y=\frac{x+1}{x-2} là đường thẳng có phương trình

A.  
x = -1
B.  
x = 1
C.  
x = -2
D.  
x = 2
Câu 15: 1 điểm

Diện tích S của mặt cầu bán kính R được tính theo công thức nào dưới đây?

A.  
S=16πR2S=16\pi {{R}^{2}}
B.  
S=43πR2S=\frac{4}{3}\pi {{R}^{2}}
C.  
S=4πR2S=4\pi {{R}^{2}}
D.  
S=πR2S=\pi {{R}^{2}}
Câu 16: 1 điểm

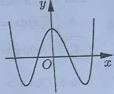
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên

Hình ảnh

A.  
y=x3−3x+1y={{x}^{3}}-3x+1
B.  
y=2x4−4x2+1y=2{{x}^{4}}-4{{x}^{2}}+1
C.  
y=−2x4+4x2+1y=-2{{x}^{4}}+4{{x}^{2}}+1
D.  
y=−x3+3x+1y=-{{x}^{3}}+3x+1
Câu 17: 1 điểm

Trên mặt phẳng tọa độ, điểm M(-3;2) là điểm biểu diễn của số phức nào dưới đây?

A.  
z4 = 3 + 2i
B.  
z2 = -3 + 2i
C.  
z1 = -3 – 2i
D.  
z3 = 3 – 2i
Câu 18: 1 điểm

Nếu ∫03f(x)dx=3\int\limits_{0}^{3}{f(x)dx=3} thì ∫032f(x)dx\int\limits_{0}^{3}{2f(x)dx} bằng

A.  
6
B.  
18
C.  
3
D.  
2
Câu 19: 1 điểm

Trong không gian Oxyz, cho mặt cầu (S) có tâm I(0;-2;1) và bán kính bằng 2. Phương trình của (S) là:

A.  
x2 + (y - 2)2 + (z + 1)2 = 2
B.  
x2 + (y - 2)2 + (z + 1)2 = 4
C.  
x2 + (y + 2)2 + (z - 1)2 = 4
D.  
x2 + (y + 2)2 + (z - 1)2 = 2
Câu 20: 1 điểm

Cho khối trụ có bán kính đáy r = 4 và chiều cao h = 3. Thể tích của khối trụ đã cho bằng

A.  
12 π\pi
B.  
36 π\pi
C.  
48 π\pi
D.  
16 π\pi
Câu 21: 1 điểm

Cho khối chóp có diện tích đáy B = 3a2 và chiều cao h = a. Thể tích của khối chóp đã cho bằng

A.  
13a3\frac{1}{3}{{a}^{3}}
B.  
3a3
C.  
32a3\frac{3}{2}{{a}^{3}}
D.  
a3
Câu 22: 1 điểm

Nghiệm của phương trình log⁡5(3x)=2{{\log }_{5}}(3x)=2 là:

A.  
x = 25
B.  
x=253x=\frac{25}{3}
C.  
x=323x=\frac{32}{3}
D.  
x = 32
Câu 23: 1 điểm

Cho hàm số f(x) = x2 + 3. Khẳng định nào dưới đây đúng?

A.  
∫f(x)dx=x3+3x+C\int{f(x)dx={{x}^{3}}+3x+C}
B.  
∫f(x)dx=2x+C\int{f(x)dx=2x+C}
C.  
∫f(x)dx=x2+3x+C\int{f(x)dx={{x}^{2}}+3x+C}
D.  
∫f(x)dx=x33+3x+C\int{f(x)dx=\frac{{{x}^{3}}}{3}+3x+C}
Câu 24: 1 điểm

Tập xác định của hàm số y=7xy={{7}^{x}} là:

A.  
R
B.  
R \ {0}
C.  
(0;+∞)\left( 0;+\infty \right)
D.  
[0;+∞)\left[ 0;+\infty \right)
Câu 25: 1 điểm

Cho hàm số y = f(x) có bảng xét dấu của đạo hàm như sau:

Hình ảnh

Số điểm cực trị của hàm số đã cho là:

A.  
2
B.  
4
C.  
3
D.  
5
Câu 26: 1 điểm

Đồ thị hàm số y = -x4 – 2x2 + 3 cắt trục tung tại điểm có tung độ bằng

A.  
2
B.  
0
C.  
3
D.  
1
Câu 27: 1 điểm

Với n là số nguyên dương bất kì, n ≥ 5, công thức nào dưới đây đúng

A.  
An5=n!5!(n−5)!A_{n}^{5}=\frac{n!}{5!(n-5)!}
B.  
An5=n!(n−5)!A_{n}^{5}=\frac{n!}{(n-5)!}
C.  
An5=5!(n−5)!A_{n}^{5}=\frac{5!}{(n-5)!}
D.  
An5=(n−5)!n!A_{n}^{5}=\frac{(n-5)!}{n!}
Câu 28: 1 điểm

Tập nghiệm của bắt phương trình 2x < 5 là

A.  
(−∞;log⁡25)\left( -\infty ;{{\log }_{2}}5 \right)
B.  
(log⁡25;+∞)\left( {{\log }_{2}}5;+\infty \right)
C.  
(log⁡52;+∞)\left( {{\log }_{5}}2;+\infty \right)
D.  
(−∞;log⁡52)\left( -\infty ;{{\log }_{5}}2 \right)
Câu 29: 1 điểm

Với mọi a, b thỏa mãn log⁡2a3+log⁡2b=8{{\log }_{2}}{{a}^{3}}+{{\log }_{2}}b=8 , khẳng nào dưới đây đúng?

A.  
a3b = 64
B.  
a3b = 256
C.  
a3 + b = 256
D.  
a3 + b = 64
Câu 30: 1 điểm

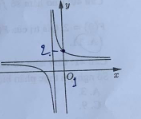
Biết hàm số y=x+ax+1y=\frac{x+a}{x+1} (a là số thực cho trước, a ≠ 1) có đồ thị như trong hình bên. Mệnh đề nào dưới đây đúng?

Hình ảnh

A.  
y′>0,∀xe−1y'>0,\forall x e -1
B.  
y′<0,∀x∈Ry'<0,\forall x\in R
C.  
y′<0,∀xe−1y'<0,\forall x e -1
D.  
y′>0,∀x∈Ry'>0,\forall x\in R
Câu 31: 1 điểm

Cho hình chóp S.ABC có đáy là tam giác vuông cân tại C, AC = 3a và SA vuông gốc với mặt phẳng đáy. Khoảng cách từ B đến mặt phẳng (SAC) bằng

A.  
32a3\sqrt{2}a
B.  
3a
C.  
32a\frac{3}{2}a
D.  
322a\frac{3\sqrt{2}}{2}a
Câu 32: 1 điểm

Trong không gian Oxyz, cho hái điểm A(0;0;1) và B(2;1;3). Mặt phẳng đi qua A và vuông góc với AB có phương trình là:

A.  
2x + y + 4z – 4 = 0
B.  
2x + y + 2z – 2 = 0
C.  
2x + y + 4z –17 = 0
D.  
2x + y + 2z – 11 = 0
Câu 33: 1 điểm

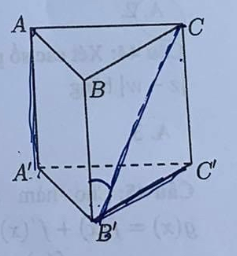
Cho hình lăng trụ đứng ABC. A’B’C’ có tất cả các cạnh bằng nhau (tham khảo hình bên). Góc giữa hai đường thẳng AA’ và B’C bằng:

Hình ảnh

A.  
450
B.  
600
C.  
300
D.  
900
Câu 34: 1 điểm

Trên đoạn [−2;1]\left[ -2;1 \right] , hàm số y = x3 – 3x2 – 1 đạt giá trị lớn nhất tại điểm

A.  
x = -1
B.  
x = 1
C.  
x = -2
D.  
x = 0
Câu 35: 1 điểm

Từ một hộp chứ 10 quả bóng gồm 4 quả màu đỏ và 6 quả màu xanh, lấy ngẫu nhiên đồng thời ba quả. Xác suất để lấy được 3 quả màu xanh bằng:

A.  
16\frac{1}{6}
B.  
35\frac{3}{5}
C.  
130\frac{1}{30}
D.  
25\frac{2}{5}
Câu 36: 1 điểm

Cho số phức z thỏa mãn iz = 6 + 5i. Số phức liên hợp của z là:

A.  
z‾=−5−6i\overline{z}=-5-6i
B.  
z‾=−5+6i\overline{z}=-5+6i
C.  
z‾=5+6i\overline{z}=5+6i
D.  
z‾=5−6i\overline{z}=5-6i
Câu 37: 1 điểm

Nếu ∫02g(x)dx=3\int\limits_{0}^{2}{g(x)dx}=3 thì ∫02[2f(x)−1]dx\int\limits_{0}^{2}{\left[ 2f(x)-1 \right]dx} bằng

A.  
4
B.  
8
C.  
6
D.  
5
Câu 38: 1 điểm

Trong không gian Oxyz, cho điểm M(2;1;-1) và mặt phẳng (P):x – 3y + 2z + 1 = 0. Đường thẳng đi qua M và vuông góc với (P) có phương trình là:

A.  
x+21=y+1−3=z−11\frac{x+2}{1}=\frac{y+1}{-3}=\frac{z-1}{1}
B.  
x−21=y−1−3=z+12\frac{x-2}{1}=\frac{y-1}{-3}=\frac{z+1}{2}
C.  
x−21=y−1−3=z+11\frac{x-2}{1}=\frac{y-1}{-3}=\frac{z+1}{1}
D.  
x+21=y+1−3=z−12\frac{x+2}{1}=\frac{y+1}{-3}=\frac{z-1}{2}
Câu 39: 1 điểm

Có bao nhiêu số nguyên x thỏa mãn (3x2−9x)[log⁡2(x+30)−5]≤0\left( {{3}^{{{x}^{2}}}}-{{9}^{x}} \right)\left[ {{\log }_{2}}(x+30)-5 \right]\le 0 ?

A.  
31
B.  
29
C.  
30
D.  
Vô số
Câu 40: 1 điểm

Cho hàm số f(x)={2x−1              khi        x≥13x2−2        khi        xlt;1f(x) = \left\{ \begin{array}{l} 2x - 1\;\;\;\;\;\;\;khi\;\;\;\;x \ge 1\\ 3{x^2} - 2\;\;\;\;khi\;\;\;\;x &lt; 1 \end{array} \right. . Giả sử F là nguyên hàm của f trên R thỏa mãn F(0)=2. Giá trị của F(-1) + 2F(2) bằng

A.  
11
B.  
6
C.  
15
D.  
9
Câu 41: 1 điểm

Cho hàm số bậc ba y = f(x) có đồ thị là đường cong trong hình bên.

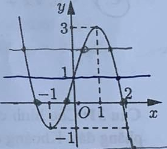
Hình ảnh

Số nghiệm thực phân biệt cả phương trình f(f(x))=1

A.  
3
B.  
6
C.  
9
D.  
7
Câu 42: 1 điểm

Cho khối hộp chữ nhật ABCD.A’B’C’D’ có đáy là hình vuông, BD = 4a, góc giữa hai mặt phẳng (A’BD) và (ABCD) bằng 300. Thể tích của khối hộp chữ nhật đã cho bằng

A.  
483a348\sqrt{3}{{a}^{3}}
B.  
1639a3\frac{16\sqrt{3}}{9}{{a}^{3}}
C.  
163a316\sqrt{3}{{a}^{3}}
D.  
1633a3\frac{16\sqrt{3}}{3}{{a}^{3}}
Câu 43: 1 điểm

Trên tập hợp các số phức, xét phương trình z2 – 2(m + 1)z + m2 = 0 (m là tham số). Có bao nhiêu giá trị của m để phương trình đó có nghiệm z0 thỏa mãn ∣z0=5∣\left| {{z}_{0}}=5 \right|

A.  
2
B.  
1
C.  
3
D.  
4
Câu 44: 1 điểm

Xét các số phức z, w thỏa mãn ∣z∣=1\left| z \right|=1 và ∣w∣=2\left| \text{w} \right|=2 . Khi ∣z+iw‾+6−8i∣\left| z+i\overline{\text{w}}+6-8i \right| đạt giá trị nhỏ nhất, ∣z−w∣\left| z-\text{w} \right| bằng

A.  
3
B.  
2215\frac{\sqrt{221}}{5}
C.  
295\frac{\sqrt{29}}{5}
D.  
5\sqrt{5}
Câu 45: 1 điểm

Cho hàm số f(x) = x3 + ax2 + bx + c với a, b, c là các số thực. Biết hàm số g(x) = f(x) + f’(x) có hai giá trị cực trị là -4 và 2. Diện tích hình phẳng giới hạn bới các đường y=f(x)g(x)+6y=\frac{f(x)}{g(x)+6} và y = 1 bằng

A.  
2ln2
B.  
3ln2
C.  
ln6
D.  
ln2
Câu 46: 1 điểm

Cắt hình nón (N) bởi mặt phẳng đi qua đỉnh và tạo mặt phẳng chứa đáy một góc bằng 600, ta được thiết diện là tam giác đều cạnh 2a. Diện tích xung quanh của (N) bằng

A.  
27πa22\sqrt{7}\pi {{a}^{2}}
B.  
13πa2\sqrt{13}\pi {{a}^{2}}
C.  
7πa2\sqrt{7}\pi {{a}^{2}}
D.  
213πa22\sqrt{13}\pi {{a}^{2}}
Câu 47: 1 điểm

Trong không gian Oxyz, cho đường thẳng d:x+11=y1=z−12d:\frac{x+1}{1}=\frac{y}{1}=\frac{z-1}{2} và mặt phẳng (P): 2x + y – z + 3 = 0. Hình chiếu vuông góc của d lên (P) là đường thẳng có phương trình:

A.  
x+13=y−5=z−11\frac{x+1}{3}=\frac{y}{-5}=\frac{z-1}{1}
B.  
x−13=y−5=z+11\frac{x-1}{3}=\frac{y}{-5}=\frac{z+1}{1}
C.  
x−14=y5=z+113\frac{x-1}{4}=\frac{y}{5}=\frac{z+1}{13}
D.  
x+14=y5=z−113\frac{x+1}{4}=\frac{y}{5}=\frac{z-1}{13}
Câu 48: 1 điểm

Có bao nhiêu số nguyên y sao cho tồn tại x∈(13;4)x\in \left( \frac{1}{3};4 \right) thỏa mãn 273x2+xy=(1+xy)2712x{{27}^{3{{x}^{2}}+xy}}=(1+xy){{27}^{12x}} ?

A.  
15
B.  
14
C.  
12
D.  
27
Câu 49: 1 điểm

Có hàm số y = f(x) có đạo hàm f’(x) = (x – 8)(x2 – 9), ∀x∈R\forall x\in R . Có bao nhiêu giá trị nguyên dương của tham số m để hàm số g(x)=f(∣x3+6x∣+m)g(x)=f\left( \left| {{x}^{3}}+6x \right|+m \right) có ít nhất 3 điểm cực trị

A.  
6
B.  
7
C.  
8
D.  
5
Câu 50: 1 điểm

Trong không gian Oxyz, Cho hai điểm A(1; -3; 2) và B(-2; 1; -3). Xét hai điểm M và N thay đổi thuộc mặt phẳng (Oxy) sao cho MN = 1. Giá trị lớn nhất của ∣AM−BN∣\left| AM-BN \right| bằng

A.  
17\sqrt{17}
B.  
61\sqrt{61}
C.  
37\sqrt{37}
D.  
41\sqrt{41}

Xem thêm đề thi tương tự

thumbnail
[2021] Bộ GD&ĐT- Mã đề 206 - Đề thi THPT QG năm 2021 môn Sinh
Chưa có mô tả

40 câu hỏi 1 mã đề 1 giờ

196,422 lượt xem 105,763 lượt làm bài

Chưa chinh phục!!!
thumbnail
[2021] Bộ GD&ĐT - Mã đề 401 - Đề thi THPT QG năm 2021 môn Tiếng Anh
Chưa có mô tả

50 câu hỏi 1 mã đề 1 giờ

197,735 lượt xem 106,470 lượt làm bài

Chưa chinh phục!!!
thumbnail
[2021] Bộ GD&ĐT- Mã đề 206 - Đề thi THPT QG năm 2021 môn Hóa học
Chưa có mô tả

40 câu hỏi 1 mã đề 1 giờ

192,030 lượt xem 103,397 lượt làm bài

Chưa chinh phục!!!
thumbnail
[2021] Bộ GD&ĐT- Mã đề 213 - Đề thi THPT QG năm 2021 môn Vật lý
Chưa có mô tả

40 câu hỏi 1 mã đề 1 giờ

195,942 lượt xem 105,504 lượt làm bài

Chưa chinh phục!!!
thumbnail
[2021] Bộ GD&ĐT - Đề minh họa kì thi tốt nghiệp THPT năm 2021 môn Tiếng Anh
Chưa có mô tả

50 câu hỏi 1 mã đề 1 giờ

219,940 lượt xem 118,426 lượt làm bài

Chưa chinh phục!!!
thumbnail
[2021] Bộ GD&ĐT - Đề minh họa kì thi tốt nghiệp THPT năm 2021 môn Hóa học
Chưa có mô tả

40 câu hỏi 1 mã đề 1 giờ

192,652 lượt xem 103,733 lượt làm bài

Chưa chinh phục!!!
thumbnail
[2021] Bộ GD&ĐT - Đề minh họa kỳ thi tốt nghiệp THPT năm 2021 môn Sinh
Chưa có mô tả

40 câu hỏi 1 mã đề 1 giờ

195,239 lượt xem 105,126 lượt làm bài

Chưa chinh phục!!!
thumbnail
[2021] Bộ GD&ĐT - Đề minh họa kì thi tốt nghiệp THPT môn Vật Lý năm 2021THPT Quốc giaVật lý
Đề minh họa kỳ thi tốt nghiệp THPT môn Vật Lý năm 2021 của Bộ Giáo dục và Đào tạo. Nội dung mang tính định hướng, giúp học sinh làm quen với cấu trúc đề thi chính thức.

40 câu hỏi 1 mã đề 1 giờ

196,467 lượt xem 105,784 lượt làm bài

Chưa chinh phục!!!
thumbnail
Đề thi thử THPT QG năm 2021 môn Toán - Bộ đề 7THPT Quốc giaToán
Đề thi thử THPT Quốc gia môn Toán năm 2021, miễn phí và có đáp án đầy đủ. Nội dung bao gồm các dạng bài trọng tâm như giải tích, số phức, logarit, và hình học không gian.

50 câu hỏi 1 mã đề 1 giờ

137,154 lượt xem 73,836 lượt làm bài

Chưa chinh phục!!!