Bài tập Toán 9 Chủ đề 3: Tứ giác nội tiếp có đáp án

Cho tam giác ABC, 2 đường cao BB’, CC’. Chứng minh tứ   giác BCB’C’ nội tiếp.

Cho đường tròn tâm O và điểm A nằm ngoài đường tròn. Kẻ hai tiếp tuyến AB, AC với đường tròn (B, C) là tiếp điểm. Trên cung nhỏ BC lấy một điểm M rồi kẻ các đường vuông góc MI, MH, MK xuống các cạnh BC, CA, AB. Gọi giao điểm của BM và IK là P; giao điểm của CM, IH là Q.

a)    Chứng minh rằng các tứ giác BIMK, CIMH nội tiếp được;

b, Chứng minh MI² = MH.MK;

Cho nửa đường tròn tâm O đường kính AB=2R và tia tiếp tuyến Ax cùng phía với nửa đường tròn đối với AB . Từ điểm M trên Ax kẻ tiếp tuyến thứ hai  MC với nửa đường tròn (C là tiếp điểm).AC cắt OM tại E  ; MB cắt nửa đường tròn (O)   tại D ( D khác B ).

a) Chứng minh: $AMCO$  và $AMDE$  là các tứ giác nội tiếp đường tròn.

b) Chứng minh MBCD là tứ giác nội tiếp (xem cách giải Bài 3)

Cho nữa đường tròn tâm O đường kính AB , kẻ tiếp tuyến Bx và lấy hai điểm C và D thuộc nửa đường tròn. Các tia  AC và AD  cắt Bx lần lượt ở E , F (  F ở giữa B và E )

1. Chứng minh: $\widehat{ABD}=\widehat{DFB}$ .

2. Chứng minh rằng CEFD là tứ giác nội tiếp.

Cho nửa đường tròn đường kính BC=2R . Từ điểm A trên nửa đường tròn vẽ $AH\perp BC$ . Nửa đường tròn đường kính BH,  CH lần lượt có tâm $O_1$ ; $O_2$  cắt $AB$ và CA  thứ tự tại D và E .

a) Chứng minh tứ giác $ADHE$  là hình chữ nhật, từ đó tính DE biết   $R=25$và  $BH=10$

b) Chứng minh tứ giác BDEC nội tiếp đường tròn.

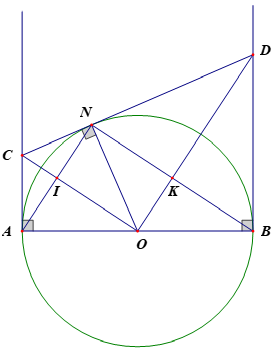
b) Chứng minh   $\Delta ANB$đồng dạng với $\Delta CMD$  từ đó suy ra $IMKN$  là tứ giác nội tiếp.

Cho tứ giác ABCD nội tiếp (O), M là điểm chính giữa của cung AB. Nối M với D, M với C cắt AB lần lượt ở E và P. Chứng minh tứ giác PEDC nội tiếp được đường tròn.

Ta có : Tứ giác ABCD nội tiếp (O) Ta phải chứng minh:  AC. BD = AB. DC + AD. BC