Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án
Đề thi Toán 12
Đề thi Toán 12 Học kì 1 có đáp án
Lớp 12;Toán
Đề thi Toán 12 Học kì 1 có đáp án
Lớp 12;Toán
Đề thi nằm trong bộ sưu tập: TOÁN 12
Số câu hỏi: 826 câuSố mã đề: 18 đềThời gian: 1 giờ
181,036 lượt xem 13,919 lượt làm bài
Chọn mã đề:
Bạn chưa làm Đề số 1!!!
Xem trước nội dung:
Câu 1: 1 điểm
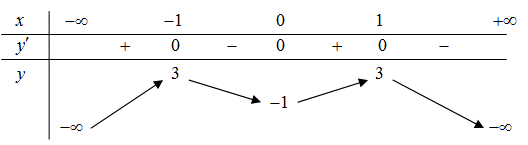
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
Hàm số đã cho đạt cực đại tại
A.
\(x = - 2\).
B.
\(x = 3\).
C.
\(x = 1\).
D.
\(x = 2\).
Câu 2: 1 điểm
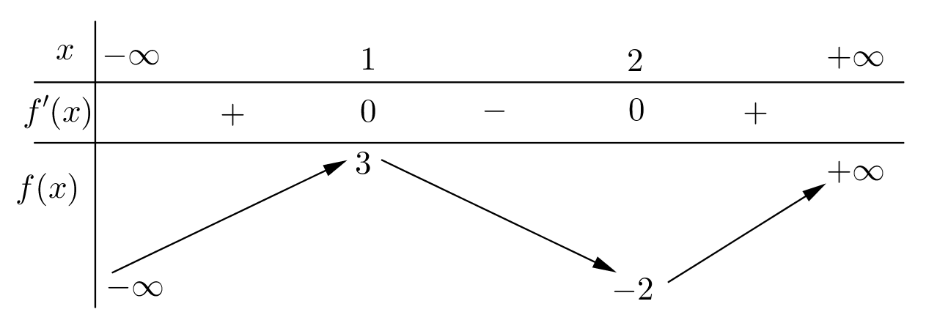
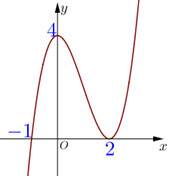
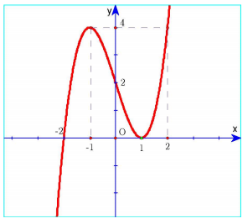
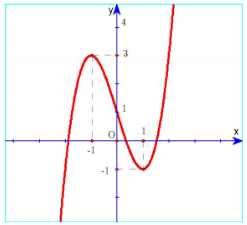
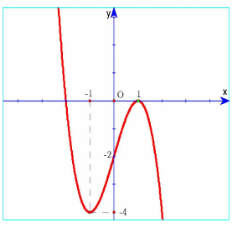
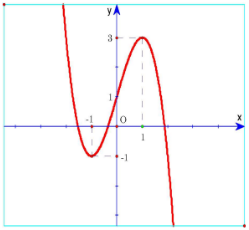
Cho hàm số \(y = f\left( x \right)\) có đồ thị hàm số như hình vẽ sau:
Giá trị nhỏ nhất của hàm số trên đoạn \(\left[ {0;4} \right]\) là
A.
\( - 3\).
B.
\(2\).
C.
\(1\).
D.
\( - 2\).
Câu 3: 1 điểm
Thể tích của khối lập phương có cạnh bằng \(4\) là:
A.
\(16.\)
B.
\(4.\)
C.
\(\frac{{64}}{3}.\)
D.
\(64.\)
Câu 4: 1 điểm
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
Giá trị lớn nhất của hàm số \(f\left( x \right)\) trên \(\mathbb{R}\) bằng
A.
\(2.\)
B.
\( - 4.\)
C.
\(3.\)
D.
\( - 1.\)
Câu 5: 1 điểm
Cho hình chóp \(S.ABCD\) có \(SA\) vuông góc với \(\left( {ABCD} \right)\), đáy \(ABCD\) là hình vuông cạnh \(a\) và \(SA = 6a\). Thể tích khối chóp \(S.ABCD\) bằng
A.
\(\frac{{{a^3}}}{3}\).
B.
\(6{a^3}\).
C.
\(3{a^3}\).
D.
\(2{a^3}\).
Câu 6: 1 điểm
Cho hàm số \(y = f\left( x \right)\) có tập xác định là \(\mathbb{R}\) và \[\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = - \infty ,\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = - 1\].
Số tiệm cận ngang của đồ thị hàm số \(y = f\left( x \right)\) là
A.
\(2\).
B.
\(0\).
C.
\(1\).
D.
\(3\).
Câu 7: 1 điểm
Đường cong trong hình bên là đồ thị của một trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
A.
\(y = \frac{{2x + 5}}{{x + 1}}\).
B.
\(y = {x^3} + 3{x^2} + 1\).
C.
\(y = \frac{{2x + 1}}{{x + 1}}\).
D.
\(y = {x^4} - {x^2} + 1\).
Câu 8: 1 điểm
Khối lăng trụ có chiều cao bằng \(4\), diện tích đáy bằng \(6\). Thể tích khối lăng trụ này bằng
A.
\(8\).
B.
\(24\).
C.
\(10\).
D.
\(12\).
Câu 9: 1 điểm
Cho hàm số \(y = f\left( x \right)\)có bảng biến thiên như sau:
Số nghiệm thực của phương trình: \(2f\left( x \right) = 3\) là
A.
\(3\).
B.
\(1\).
C.
\(2\).
D.
4.
Câu 10: 1 điểm
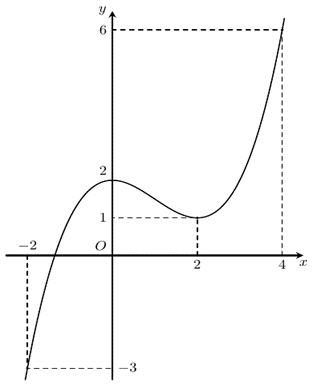
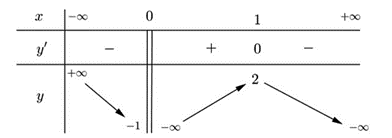
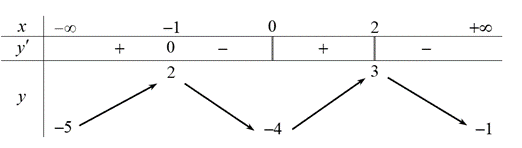
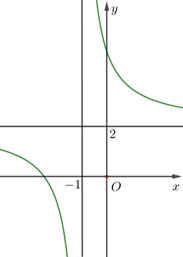
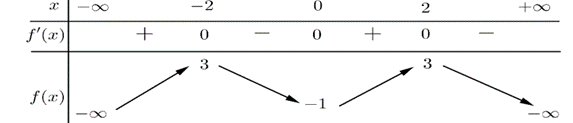
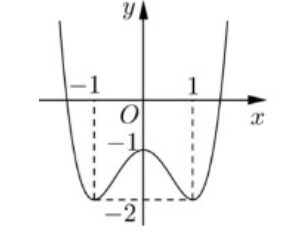
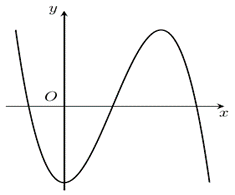
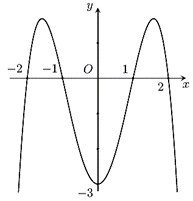
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\)có đồ thị như hình vẽ sau.
Số điểm cực tiểu của của hàm số \(y = f\left( x \right)\)
A.
\(0\).
B.
\(1\).
C.
\(2\).
D.
\(3\).
Câu 11: 1 điểm
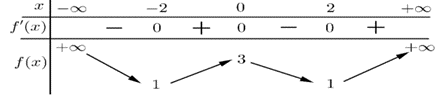
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
\(\left( {0;2} \right)\).
B.
\(\left( {1;3} \right)\).
C.
\(\left( { - 2;0} \right)\)
D.
\(\left( {1; + \infty } \right)\).
Câu 12: 1 điểm
Khối chóp có chiều cao bằng \(3\), diện tích đáy bằng \(5\). Thể tích khối chóp bằng:
A.
\(15\).
B.
\(5\).
C.
\(8\).
D.
\(25\).
Câu 13: 1 điểm
Số cạnh của một hình bát diện đều là
A.
\(12\).
B.
\(16\).
C.
\(10\).
D.
\(8\).
Câu 14: 1 điểm
Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị như hình sau
Hàm số \(y = f\left( x \right)\) nghịch biến trên khoảng nào dưới đây?
A.
\(\left( {0;2} \right)\).
B.
\(\left( { - \infty ; - 1} \right)\).
C.
\(\left( {2;4} \right)\).
D.
\(\left( { - 1;2} \right)\).
Câu 15: 1 điểm
Đường cong trong hình vẽ sau là đồ thị của hàm số nào dưới đây?
A.
\[y = - {x^3} + 3{x^2} - 2\].
B.
\[y = - {x^4} + {x^2} - 2\].
C.
\[y = {x^4} - {x^2} - 2\].
D.
\[y = {x^3} - 3{x^2} - 2\].
Câu 16: 1 điểm
Cho hàm số \(y = f\left( x \right)\) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên dưới đây. Đồ thị hàm số \(y = f\left( x \right)\) cắt đường thẳng \(y = - 2020\) tại bao nhiêu điểm?
A.
\[0\].
B.
\[4\].
C.
\[2\].
D.
\[1\].
Câu 17: 1 điểm
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\backslash \left\{ 0 \right\}\), liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
Hỏi đồ thị hàm số trên có bao nhiêu đường tiệm cận?
A.
1.
B.
0.
C.
2.
D.
3.
Câu 18: 1 điểm
Hình đa diện nào dưới đây không có tâm đối xứng?
A.
Bát diện đều.
B.
Tứ diện đều.
C.
Hình lập phương.
D.
Lăng trụ lục giác đều.
Câu 19: 1 điểm
Hàm số nào sau đây đồng biến trên \(\mathbb{R}\)?
A.
\(y = \frac{{2x - 1}}{{x + 3}}\).
B.
\(y = {x^3} + 2x\).
C.
\(y = 2{x^2} + 1\).
D.
\(y = 2{x^4} + {x^2}\).
Câu 20: 1 điểm
Giá trị nhỏ nhất của hàm số \(f\left( x \right) = {x^3} - 3x\) trên đoạn \(\left[ { - 3\,;\,3} \right]\) bằng
A.
\(18\).
B.
\(2\).
C.
\( - 2\).
D.
\( - 18\).
Câu 21: 1 điểm
Giá trị lớn nhất của hàm số \(f\left( x \right) = \sqrt {11 - 2x} \) trên \(\left[ {1;5} \right]\) bằng
A.
\[3\].
B.
\[\sqrt 5 \].
C.
\[1\].
D.
\[\sqrt {11} \].
Câu 22: 1 điểm
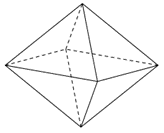
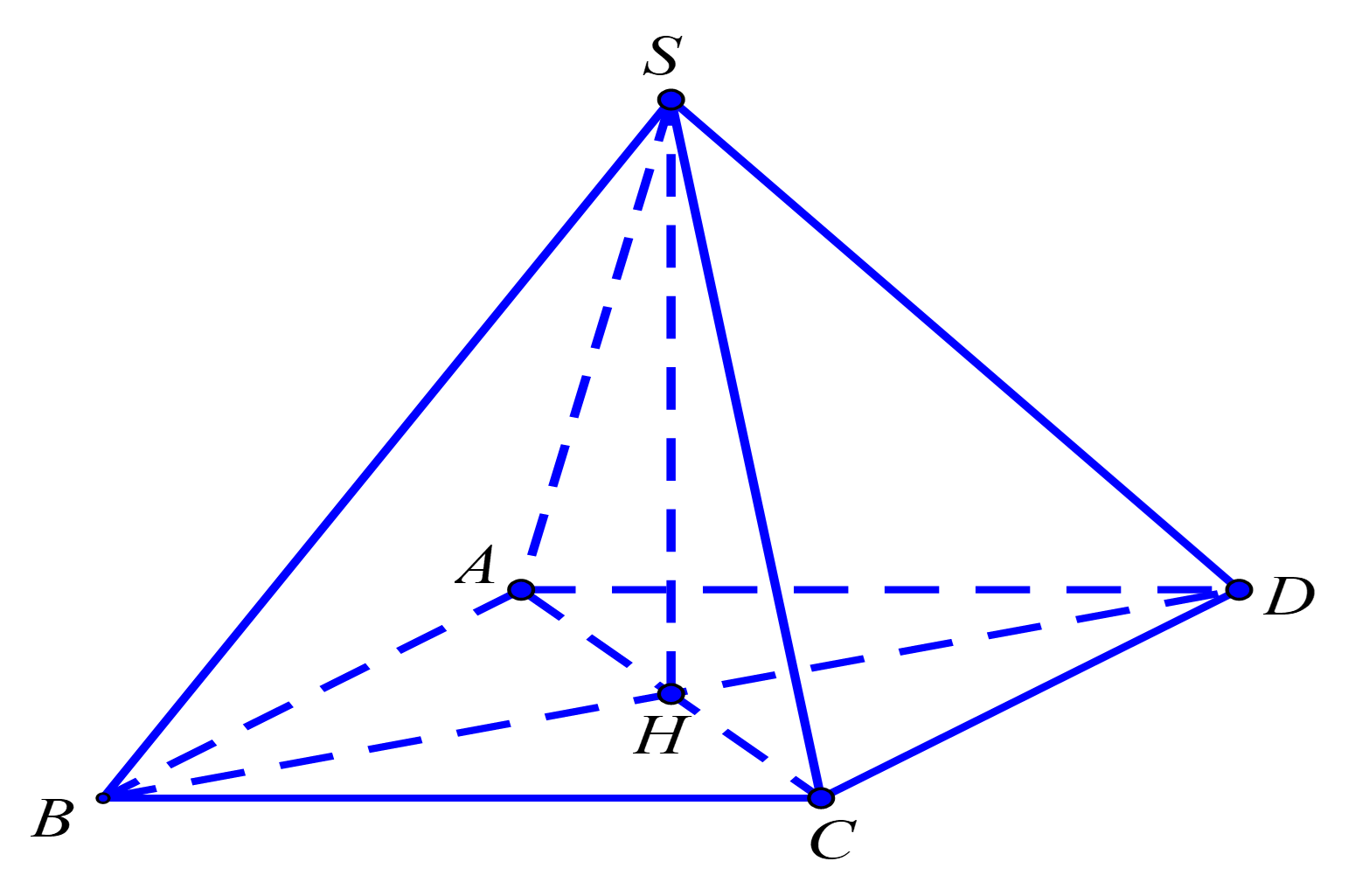
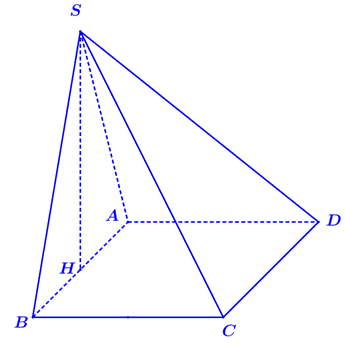
Cho \(S.ABCD\)là hình chóp tứ giác đều, biết \[AB = a,\,\,SA = a\]. Thể tích của khối chóp \(S.ABCD\) bằng
A.
\[\frac{{{a^3}\sqrt 2 }}{2}\].
B.
\[\frac{{{a^3}}}{3}\].
C.
\[\frac{{{a^3}\sqrt 2 }}{6}\].
D.
\[{a^3}\].
Câu 23: 1 điểm
Cho hàm số \(y = \frac{{x + 1}}{{x - 1}}.\) Khẳng định nào sau đây là khẳng định đúng?
A.
Hàm số đồng biến trên các khoảng \(\left( { - \infty ;\,1} \right)\) và \(\left( {1;\, + \infty } \right).\)
B.
Hàm số nghịch biến trên \(\mathbb{R}.\)
C.
Hàm số đồng biến trên \(\mathbb{R}.\)
D.
Hàm số nghịch biến trên các khoảng \(\left( { - \infty ;\,1} \right)\) và \(\left( {1;\, + \infty } \right).\)
Câu 24: 1 điểm
Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right),\) đáy \(ABCD\) là hình chữ nhật. Biết \(AB = a,\) \(AD = 2a,\) \(SA = 3a.\) Thể tích hình chóp \(S.ABCD\) bằng
A.
\(2{a^3}.\)
B.
\(6{a^3}.\)
C.
\({a^3}.\)
D.
\(\frac{{{a^3}}}{3}.\)
Câu 25: 1 điểm
Đồ thị hàm số \(y = {x^3} - 3x + 2\) là hình nào trong 4 hình dưới đây?
A.
A. 
.
.B.
B. 
.
.C.
C. 
.
.D.
D. 
.
. Câu 26: 1 điểm
Đồ thị hàm số nào sau đây không có tiệm cận đứng?
A.
\(y = \frac{1}{{{x^2} + 2x + 1}}\).
B.
\(y = \frac{{\sqrt {x - 3} }}{{x + 2}}\).
C.
\(y = - \frac{1}{x}\).
D.
\(y = \frac{{3x - 1}}{{{x^2} - 1}}\).
Câu 27: 1 điểm
Lăng trụ đứng \[ABCA'B'C'\] có đáy \[ABC\] là tam giác vuông tại \[A\], \[BC = 2a,{\rm{ }}AB = a\]. Mặt bên \[(BB'C'C)\] là hình vuông. Khi đó thể tích lăng trụ là
A.
\[{a^3}\sqrt 2 \].
B.
\[{a^3}\sqrt 3 \].
C.
\[2{a^3}\sqrt 3 \].
D.
\[\frac{{{a^3}\sqrt 3 }}{3}\].
Câu 28: 1 điểm
Tìm phương trình tất cả các tiệm cận của đồ thị hàm số: \[y = \frac{{3x - 1}}{{x - 2}}\]
A.
\[x = - 2\] và \[y = 3\].
B.
\[x = 3\] và \[y = 2\].
C.
\[x = 2\] và \[y = - \frac{1}{2}\].
D.
\[x = 2\] và \[y = 3\].
Câu 29: 1 điểm
Cho hàm số \(f\left( x \right)\) có đạo hàm\(f'\left( x \right) = x{\left( {x + 1} \right)^2},\forall x \in \mathbb{R}\). Số điểm cực trị của hàm số đã cho là
A.
\(2\).
B.
\(0\).
C.
\(1\).
D.
\(3\).
Câu 30: 1 điểm
Hình chóp \(S.ABCD\) đáy hình vuông, \(SA\) vuông góc với đáy, \(SA = a\sqrt 3 ,AC = a\sqrt 2 \). Khi đó thể tích khối chóp \(S.ABCD\) là
A.
\(\frac{{{a^3}\sqrt 3 }}{2}\).
B.
\(\frac{{{a^3}\sqrt 2 }}{2}\).
C.
\(\frac{{{a^3}\sqrt 3 }}{3}\).
D.
\(\frac{{{a^3}\sqrt 2 }}{3}\).
Câu 31: 1 điểm
Cho hàm số \(y = a{x^4} + b{x^2} + c\)có đồ thị như hình vẽ sau. Trong các mệnh đề dưới đây, mệnh đề nào đúng?
A.
\(a > 0,b < 0,c < 0\).
B.
\(a < 0,b < 0,c < 0\).
C.
\(a < 0,b > 0,c < 0\).
D.
\(a > 0,b < 0,c > 0\).
Câu 32: 1 điểm
Số cực trị của hàm số \(f(x) = {x^4} - 4{x^2} + 3\)
A.
\(2\).
B.
\(3\).
C.
\(4\).
D.
\(1\).
Câu 33: 1 điểm
Trong tất cả các loại hình đa diện đều sau, loại nào có số mặt nhiều nhất?
A.
\[\left\{ {5;3} \right\}\].
B.
\[\left\{ {3;5} \right\}\].
C.
\[\left\{ {4;3} \right\}\].
D.
\[\left\{ {3;4} \right\}\].
Câu 34: 1 điểm
Số giao điểm của đồ thị hàm số \[y = {x^3} - 5x\] và đường thẳng \[y = x\] là
A.
\[0\].
B.
\[3\].
C.
\[2\].
D.
\[1\].
Câu 35: 1 điểm
Hàm số \(y = f(x)\) và có đồ thị như hình sau. Số nghiệm thực của phương trình \(3f(x) - 5 = 0\) trên đoạn \(\left[ {0;4} \right]\) là:
A.
2.
B.
0.
C.
3.
D.
1.
Câu 36: 1 điểm
Một vật chuyển động theo quy luật \(S = - \frac{1}{2}{t^3} + 9{t^2},\) với \(t\)(giây) là khoảng thời gian tính từ
lúc vật bắt đầu chuyển động và \(s\)(mét) là quãng đường vật đi được trong thời gian đó. Hỏi trong khoảng thời gian 10 giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng:
A.
\(400\)(m/s).
B.
\(216\)(m/s).
C.
30(m/s).
D.
54(m/s).
Câu 37: 1 điểm
Xác định \[a,\,b,\,c\]để hàm số \(y = \frac{{ax - 1}}{{bx + c}}\) có đồ thị như hình vẽ bên. Chọn đáp án đúng?
A.
\(a = 2,\,b = 2,\,c = - 1\).
B.
\(a = 2,\,b = 1,\,c = 1\).
C.
\(a = 2,\,b = - 1,\,c = 1\).
D.
\(a = 2,\,b = 1,\,c = - 1\).
Câu 38: 1 điểm
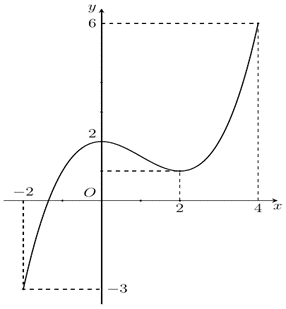
Cho hàm số \(y = f\left( x \right)\)có đạo hàm trên \(\mathbb{R}\)và có đồ thị như hình vẽ sau:
Số cực trị của hàm số \(y = {\left[ {f\left( x \right)} \right]^2}\) là
A.
\(5\).
B.
\(3\).
C.
\(1\).
D.
\(4\).
Câu 39: 1 điểm
Tìm tất cả các giá trị thực của tham số \[m\] sao cho hàm số \[y = \frac{{mx + 9}}{{x + m}}\] nghịch biến trên từng khoảng xác định
A.
\[ - 3 \le m \le 3\].
B.
\[ - 3 < m < 3\].
C.
\[ - 3 \le m < 3\].
D.
\[ - 3 < m \le 3\].
Câu 40: 1 điểm
Tập tất cả các giá trị thực của tham số \[m\] để hàm số \[y = {x^3} - \left( {m - 1} \right){x^2} + 3x + 1\] đồng biến trên khoảng \[\left( { - \infty ; + \infty } \right)\] là
A.
\[\left( { - 2\,;\,4} \right)\].
B.
\[\left( { - \infty \,;\, - 2} \right) \cup \left( {4\,;\, + \infty } \right)\].
C.
\[\left[ { - 2\,;\,4} \right]\].
D.
\[\left( { - \infty \,;\, - 2} \right] \cup \left[ {4\,;\, + \infty } \right)\].
Câu 41: 1 điểm
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\backslash \left\{ 0 \right\}\)và có bảng biến thiên như
hình sau.
Số nghiệm của phương trình: \(f\left( {{x^2}} \right) = 1\)
A.
\(2\).
B.
\(3\).
C.
\(4\).
D.
\(6\).
Câu 42: 1 điểm
Tìm tất cả các giá trị thực của \(m\) để hàm số \(y = m{x^4} - \left( {m + 1} \right){x^2} + 2m - 1\) có 3 điểm cực trị?
A.
\( - 1 < m < 0\).
B.
\(m < - 1\).
C.
\(m > - 1\).
D.
\(\left[ \begin{array}{l}m < - 1\\m > 0\end{array} \right.\).
Câu 43: 1 điểm
Cho lăng trụ \(ABC.A'B'C'\). Gọi \(M,N\) lần lượt là trung điểm của \(BB'\) và \(CC'\). Tỉ số thể tích \(\frac{{{V_{ABCMN}}}}{{{V_{ABC.A'B'C'}}}}\) là
A.
\(\frac{1}{6}\).
B.
\(\frac{1}{3}\).
C.
\(\frac{1}{2}\).
D.
\(\frac{2}{3}\).
Câu 44: 1 điểm
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \(y = \frac{{\sqrt {x + 4} - 2}}{{{x^2} + x}}\) là
A.
1.
B.
4.
C.
2.
D.
3.
Câu 45: 1 điểm
Cho hình chóp \(S.ABC\) có đáy là tam giác vuông tại \(B\). Biết \(\Delta SAB\) là tam giác đều và thuộc mặt phẳng vuông góc với mặt phẳng \(\left( {ABC} \right)\). Biết \(AB = a\), \(AC = a\sqrt 3 \). Thể tích khối chóp \(S.ABC\) là:
A.
\(\frac{{{a^3}}}{4}\).
B.
\(\frac{{{a^3}\sqrt 6 }}{4}\).
C.
\(\frac{{{a^3}\sqrt 2 }}{6}\).
D.
\(\frac{{{a^3}\sqrt 6 }}{{12}}\).
Câu 46: 1 điểm
Cho hình chóp tứ giác \[S.ABCD\] có đáy là hình vuông, mặt bên \[\left( {SAB} \right)\] là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Biết khoảng cách từ điểm \[A\] đến mặt phẳng \[\left( {SCD} \right)\] bằng \(a\sqrt 3 \). Tính thể tích \(V\) của khối chóp \(S.ABCD\).
A.
\(V = \frac{{7{a^3}\sqrt {21} }}{6}\).
B.
\(V = \frac{{7{a^3}\sqrt {21} }}{2}\).
C.
\(V = \frac{{7{a^3}\sqrt 7 }}{6}\).
D.
\(V = \frac{{3{a^3}\sqrt 7 }}{2}\).
Câu 47: 1 điểm
Cho hình lăng trụ đứng \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác vuông tại \(B\), \(BC = a\), mặt phẳng \(\left( {A'BC} \right)\) tạo với đáy một góc \({30^ \circ }\) và tam giác \(A'BC\) có diện tích bằng \({a^2}\sqrt 3 \). Thể tích khối lăng trụ \(ABC.A'B'C'\) bằng
A.
\(\frac{{{a^3}\sqrt 3 }}{8}\).
B.
\(\frac{{3{a^3}\sqrt 3 }}{2}\).
C.
\(\frac{{3{a^3}\sqrt 3 }}{8}\).
D.
\(\frac{{3{a^3}\sqrt 3 }}{4}\).
Câu 48: 1 điểm
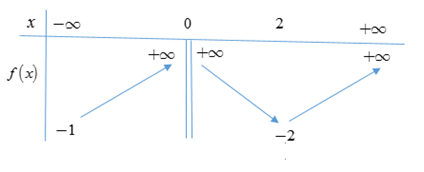
Cho hàm số \(f(x)\), có bảng biến thiên của hàm số \(f'(x)\) như sau:
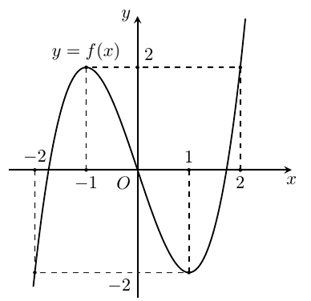
Số cực trị của hàm số \(y = f({x^2} + 2x)\) là
A.
\(5\).
B.
\(4\).
C.
\(3\).
D.
\(7\).
Câu 49: 1 điểm
Cho hàm số \(y = f\left( x \right)\), có bảng xét dấu \(f'\left( x \right)\) như sau:
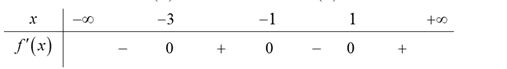
Hàm số \(y = f\left( {3 - 2x} \right)\) đồng biến trên khoảng nào dưới đây?
A.
\(\left( {3\,;\, + \infty } \right)\).
B.
\(\left( {2\,;\,4} \right)\).
C.
\(\left( {1\,;\, + \infty } \right)\).
D.
\(\left( { - \infty \,;\,1} \right)\).
Câu 50: 1 điểm
Cho các số thực không âm \(x,y\) thỏa mãn \(x + y = 1\). Giá trị lớn nhất \(M\) và giá trị nhỏ nhất \(m\) của biểu thức \(S = \left( {4{x^2} + 3y} \right)\left( {4{y^2} + 3x} \right) + 25xy\) lần lượt là
A.
\(M = \frac{{25}}{2},m = 12\).
B.
\(M = 12,m = \frac{{191}}{{16}}\).
C.
\(M = \frac{{25}}{2},m = \frac{{191}}{{16}}\)
D.
\(M = \frac{{25}}{2},m = 0\).
Đề thi tương tự
Bộ 20 đề thi giữa học kì 1 Toán 12 năm 2022-2023 có đáp án
24 mã đề 1037 câu hỏi 1 giờ
190,467 xem14,645 thi
Bộ 20 đề thi giữa học kì 1 Toán 11 năm 2022 - 2023 có đáp án
17 mã đề 757 câu hỏi 1 giờ
148,083 xem11,384 thi
Bộ 20 đề thi giữa kì 2 Toán 12 có đáp án năm 2022-2023
20 mã đề 883 câu hỏi 1 giờ
154,969 xem11,914 thi
Bộ 20 đề thi học kì 1 Toán lớp 4 có đáp án (Mới nhất)
20 mã đề 359 câu hỏi 1 giờ
182,268 xem14,013 thi
Bộ 20 đề thi học kì 1 Toán 11 năm 2022 - 2023 có đáp án
19 mã đề 488 câu hỏi 1 giờ
176,392 xem13,563 thi
Bộ 20 đề thi trắc nghiệm Học kì 1 môn Toán lớp 4 (Có đáp án)
19 mã đề 182 câu hỏi 1 giờ
159,987 xem12,298 thi
Bộ 20 đề thi ôn luyện THPT Quốc gia môn Vật lí có lời giải 2022
20 mã đề 800 câu hỏi 1 giờ
267,168 xem20,544 thi
20 Bộ đề thi thử THPT quốc gia môn Vật Lí cực hay có lời giải
14 mã đề 560 câu hỏi 1 giờ
227,958 xem17,528 thi
Tuyển tập 20 bộ đề thi thử THPTQG Hóa Học cực hay có lời giải
20 mã đề 797 câu hỏi 1 giờ
341,081 xem26,233 thi