Đề thi thử tốt nghiệp THPT QG môn Toán năm 2020 - Bộ đề 15

Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình sau?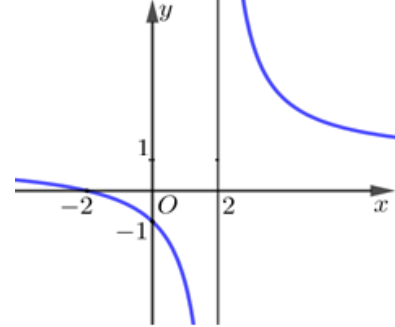

Cho hình chóp S. ABC có $S A=S B\,\, và \,\,C A=C B$ . Góc giữa hai đường thẳng SC và AB bằng

Giá trị lớn nhất của hàm số y=\frac{3 x-1}{x-3}\)-trên \([0 ; 2] là:

Số nghiệm của phương trình $\log _{2}\left(x^{2}-x+2\right)=1$ là:

Cho lăng trụ đều ABC.A' B'C' có cạnh đáy bằng 2a, độ dài cạnh bên bằng $a \sqrt{3}$ . Tính thể tích V của khối lăng trụ

Cho a là số thực dương khác 1 . Tính $I=\log _{\sqrt{a}} a$

Tính thể tích V của khối chóp có đáy là hình vuông cạnh bằng 3 và chiều cao bằng 4

Hàm số $y=x^{4}-2 x^{2}+1$nghịch biến trên khoảng nào sau đây?

Thể tích khối cầu có bán kính r bằng

Cho số phức $z=2-3 i$ . Phần ảo của số phức z là.

Xét số phức z thỏa mãn $(\bar{z}+2 i)(z-2)$là số thuần ảo. Trên mặt phẳng tọa độ, tập hợp tất cả các điểm biễu diễn các số phức z là một đường tròn có tâm là điểm nào dưới đây?

Nếu $\int\limits_{1}^{2} f(x) d x=5 \text { và } \int\limits_{1}^{2} g(x) d x=-7 \text { thì } \int\limits_{1}^{2}(2 f(x)+g(x)) d x$ bằng

Họ tất cả các nguyên hàm của hàm số $f(x)=3 x^{2}+\frac{1}{x}$ là:

Trên mặt phẳng tọa độ, điểm biểu diễn số phức liên hợp của số phức $z=3+4 i$ là điểm nào dưới dây?

Tính diện tích xung quanh của hình nón có bán kính đáy $r=\sqrt{3}$ và chiều cao h = 4

Quay hình vuông ABCD cạnh a xung quanh một cạnh .Thể tích khối trụ được tạo thành là:

Cho cấp số nhân (u_n )\) có \(u_{2}=\frac{1}{4} \text { và } u_{3}=1. Tìm công bội q

Trong không gian Oxyz , cho đường thẳng $d: \frac{x-1}{2}=\frac{y+1}{1}=\frac{z-1}{2}$. Véc tơ nào sau đâu là véc tơ chỉ phương của đường thẳng d

Cho số phức $z=2+i . \operatorname{Tính }|z|$

Có bao nhiêu cách để 10 người ngồi vào 10 ghế xếp thành hàng dài sao cho mỗi người ngồi đúng một ghế ?

Tập nghiệm của bất phương trình e^{x^{2}-x+1}<e

Tổng số đường tiệm cận ngang của đồ thị hàm số $y=\frac{2 x-1}{x+1}$

Tìm tập xác định D của hàm số $y=(2-x)^{\frac{1}{3}}$

Cho lăng trụ tam giác đều A B C \cdot A^{\prime} B^{\prime} C^{\prime}\) có độ dài cạnh đáy bằng a, góc giữa đường thẳng AB' và mặt phẳng (ABC) bằng \(60^{\circ} . . Tính thể tích V của khối trụ ngoại tiếp lăng trụ đã cho

Cho a=\log _{2} 5, b=\log _{2} 9\). Biểu diễn của \(P=\log _{2} \frac{40}{3} theo a và b là

Tính thể tích vật thể giới hạn bởi các mặt phẳng x =0 và x= 1, biết thiết diện của vật thể cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoàng độ 0 \leq x \leq 1\) là một hình vuông có độ dài cạnh \(\sqrt{x (e^{x}-1)}.

Tất cả các giá trị của m để hàm số y=\frac{2 \cos x-1}{\cos x-m}\) đồng biến trên khoảng \(\left(0 ; \frac{\pi}{2}\right) là

Cho hàm số y =f(x) có đồ thị như sau

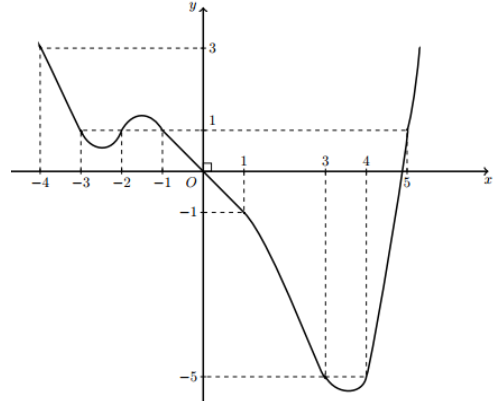
Số nghiệm thực của phương trình $f(|x|)-1=0$ là

COVID19 là một loại bệnh viêm đường hô hấp cấp do chủng mới virus corona (nCOV) bắt đầu từ Trung Quốc (đầu tháng 12/2019) gây ra với tốc độ truyền bệnh rất nhanh (tính đến ngày 02/06/2020 đã có 6.365.173 người nhiễm bệnh. Giả sử ban đầu có 1 người nhiễm bệnh và cứ sau 1 ngày sẽ lây sang a người khác ($a \in \mathbb{N}^{*}$ ). Tất cả những người nhiễm bệnh lại lây sang những người khác với tốc độ như trên (1 người lây cho a người). Tìm a biết sau 7 ngày có 16384 người mắc bệnh. (Giả sử người nhiễm bệnh không phát hiện bản thân bị bệnh, không phòng tránh cách ly và trong thời gian ủ bệnh vẫn lây sang người khác được)

Trong không gian Oxyz , cho điểm $A(1 ;-3 ; 2)$ Tọa độ điểm A' đối xứng với A điểm qua mặt phẳng (Oyz) là

Biết rằng hàm số $y=f(x)=a x^{4}+b x^{2}+c$ có đồ thị là đường cong trong hình vẽ dưới đây.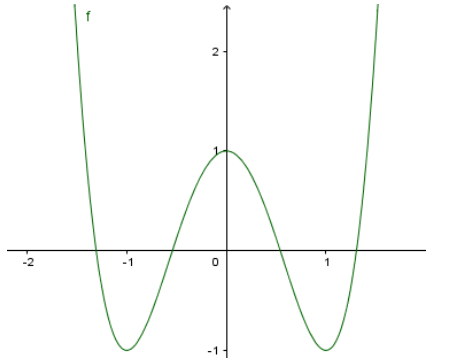

Tính a+b+2c

Tập nghiệm của bất phương trình $\log _{2}^{2} x-5 \log _{2} x-6 \geq 0$ là:

Cho hình chóp S . A B C D\) có đáy là hình thoi cạnh a ,\(\widehat{ B A D}=60^{\circ},S B=S D=S C , M là trung điểm của SD , H là hình chiếu của S trên mặt phẳng (ABCD). Tính khoảng cách giữa hai đường thẳng SH và CM

Trong không gian Oxyz , mặt phẳng đi qua điểm M (1;2;3) và song song với mặt phẳng $(P): x-2 y+z-3=0$ có phương trình là

Cho hàm số $y=x^{3}-3 x^{2}+9$ có đồ thị là (C). Điểm cực tiểu của đồ thị (C) là

Trong không gian Oxyz cho mặt cầu (S) có tâm là I (0;0;1) và tiếp xúc với mặt phẳng $(\alpha): 2 x-2 y+z+8=0$ . Phương trình của (S ) là

Gọi Alà tập các số tự nhiên có 5 chữ số đôi một khác nhau được lập từ các số 1;2;3;4;5;6;7;8;9. Lấy ngẫu nhiên một số thuộc tập A. Tính xác suất để số lấy được luôn có mặt hai chữ số 1;2 và chúng không đứng cạnh nhau

Gọiz_1, z_2\) , là các nghiệm phức của phương trình\(z^{2}+z+1=0, \text { đặt } \mathrm{w}=z_{1}^{2021}+z_{2}^{2021}1 Khi đó

Trong không gian Oxyz , phương trình mặt phẳng trung trực của đoạn thẳng AB với $A(3 ;-2 ; 1) \text { và } B(1 ; 0 ; 5)$ là:

Cho đường thẳng d: \frac{x-2}{-1}=\frac{y+1}{-1}=\frac{z+1}{1}\)-và mặt phẳng \((P): 2 x+y-2 z=0\). Đường thẳng \(\Delta nằm trong (P), cắt d và vuông góc với d có phương trình là:

Gọi F x ( ) là nguyên hàm của hàm số $f(x)=\frac{x}{\sqrt{8-x^{2}}}$ thỏa mãn F(2)=0 . Khi đó phương trình F(x)=x có nghiệm là:

Cho hình chóp S.ABCD có đáy là hình vuông cạnh 3a . Hình chiếu vuông góc của S trên mặt phẳng đáy ABCD là điểm H thuộc cạnh AB sao cho HB=2.HA . Cạnh SA hợp với mặt phẳng đáy góc $60^0$ . Tính diện tích mặt cầu ngoại tiếp hình chóp S ABCD

Gọi S là tập hợp tất cả các giá trị của tham số m để hàm sốf x=m^{2}\left(\frac{e^{5 x}}{5}-16 e^{x}\right)+3 m\left(\frac{e^{3 x}}{3}-4 e^{x}\right)-14\left(\frac{e^{2 x}}{2}-2 e^{x}\right)+2020\) đồng biến trên \(\mathbb{R} . Tổng của tất cả các phần tử thuộc S bằng:

Cho hàm số y=f(x) có đồ thị như hình sau:

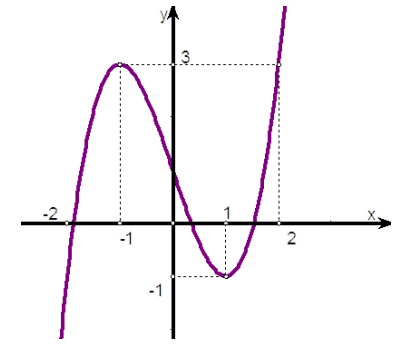
Gọi S là tập hợp các giá trị nguyên của tham số m để phương trình f(3 \sin x+m)-3=0\)có đúng 6 nghiệm phân biệt thuộc \([0 ; 3 \pi] Tổng các phần tử của S bằng

Cho hình chóp S .ABCD có đáy là hình thang vuông tại A và B , S A \perp(A B C D), A D=3 a\), \(S A=A B=B C=a\) . Gọi S ' là điểm thỏa mãn \(\overrightarrow{S S^{\prime}}=\frac{1}{2} \overrightarrow{A B}\). Tính thể tích khối đa diện \(S S^{\prime} A B C D

Cho hàm số y=f(x) liên tục trên $\mathbb{R}$ và có đồ thị như hình vẽ.

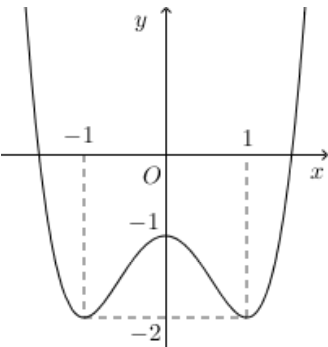
Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số y=f(\cos x)-2 \cos x-m\) cắt trục hoành tại điểm có hoành độ thuộc khoảng \(\left(-\frac{\pi}{2} ; \frac{\pi}{2}\right)

Cho x, y, zlà các số thực không âm thoả mãn 12^{x}+2^{y}+2^{z}=10\) . Giá trị lớn nhất của biểu thức \(P=x+y+3 zgần nhất với số nào sau đây?

Cho hàm số f(x) liên tục trên \mathbb{R}\) thỏa mãn \(f(x)=\left\{\begin{array}{ll} x+m & \text { khi } x \geq 0 \\ c^{2 x} & \text { khi } x<0 \end{array}\right.\) (m là hằng số). Biết \(\int_{-1}^{2} f(x) \mathrm{d} x=a+b . c^{-2} . trong đó a b , là các số hữu tỷ. Tính a + b

Cho hàm số f x ( ) có bảng biến thiên như sau: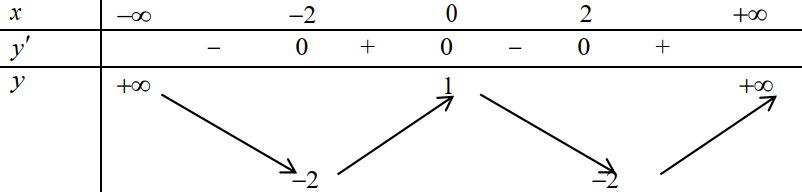

Gọi $g(x)=\| 2 f(x)-2|+f(x)+10-m|$ có tổng giá trị nhỏ nhất và giá trị lớn nhất trên đoạn [-2 ; 2] bằng 2. Tính tích các phần tử của S .

Cho Hàm số f(x) liên tục trên $\mathbb{R}$ và có đồ thị hàm số y =f'(x)như hình vẽ bên dưới

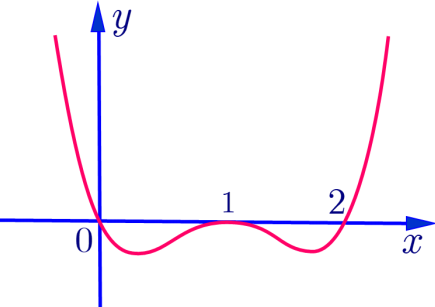
Hàm số $g(x)=f\left(\frac{5 x}{x^{2}+4}\right)$ có bao nhiêu điểm cực đại?