Trắc nghiệm Đường thẳng và mặt phẳng song song có đáp án (Nhận biết)

Số điểm chung của đường thẳng và mặt phẳng không thể là:

Nếu đường thẳng d và mặt phẳng $\left(\alpha \right)$không có điểm chung thì chúng

Cho đường thẳng d và mặt phẳng (α) như hình vẽ, số điểm chung của d và (α) là:

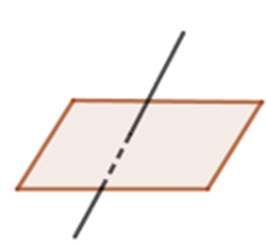
Nếu một đường thẳng d không nằm trong mặt phẳng (α) mà nó song song với đường thẳng d’ trong (α) thì:

Mệnh đề nào dưới đây đúng?

Cho các mệnh đề sau:

1. Nếu a // (P) thì a song song với mọi đường thẳng nằm trong (P)

2. Nếu a // (P) thì a song song với một đường thẳng nào đó nằm trong (P)

3. Nếu a // (P) thì có vô số đường thẳng nằm trong (P) và song song với a

4. Nếu a // (P) thì có một đường thẳng d nào đó nằm trong (P) sao cho a và d đồng phẳng.

Số mệnh đề đúng là:

Cho $d//\left(\alpha \right)$và $d^{\text{'}}\subset \left(\alpha \right)$, số giao điểm của d và d’ là:

Cho hai đường thẳng chéo nhau, số mặt phẳng chứa đường thẳng này mà song song đường thẳng kia có thể là:

Hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Gọi O và O’ lần lượt là tâm hình bình hành ABCD và ABEF. OO’ song song với:

Cho đường thẳng a song song với mặt phẳng (P). Khi đó, số đường thẳng phân biệt nằm trong (P) và song song với a có thể là:

Cho hai đường thẳng a, b song song với nhau. Hai mặt phẳng (P), (Q) phân biệt tương ứng chứa a, b đồng thời cắt nhau theo giao tuyến d. Khi đó đường thẳng d:

Cho trước hai đường thẳng a và b chéo nhau. Khi đó:

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi d là giao tuyến của hai mặt phẳng (SAD) và (SBC). Khẳng định nào sau đây là đúng?

Cho hình lập phương ABCD.A'B'C'D', AC và BD cắt nhau tại O, A'C' và B'D' cắt nhau tại O'. Các điểm M, N, P theo thứ tự là trung điểm của AB, BC, O'B'. Khi đó thiết diện do mặt phẳng (MNP) cắt hình lập phương sẽ là đa giác có số cạnh là bao nhiêu?

Nếu đường thẳng $d//\left(\alpha \right)$và $d\text{'}\subset \left(\alpha \right)$thì d và d’ có thể: