Trắc nghiệm Ôn tập chương II Hình học 12 có đáp án

Cho mặt cầu (S). Nếu (P) là mặt phẳng kính của mặt cầu (S) thì:

Khi quay hình chữ nhật ABCD quanh các cạnh nào dưới đây ta được hai hình trụ có cùng chiều cao?

Khi quay hình chữ nhật MNPQ quanh đường thẳng AB với A, B lần lượt là trung điểm của MN, PQ ta được một hình trụ có đường kính đáy:

Cho hình chữ nhật ABCD. Gọi M, N lần lượt là trung điểm các cạnh AB, CD. Quay hình chữ nhật quanh trục MN ta được hình trụ có bán kính đáy là:

Một hình hộp chữ nhật có độ dài 3 cạnh lần lượt là 2, 2, 1. Tính bán kính R mặt cầu ngoại tiếp hình hộp nói trên.

Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB=a, AD=2a, AA'=2a. Tính bán kính R của mặt cầu ngoại tiếp tứ diện ABB’C’

Một hình nón có thiết diện qua trục là tam giác đều cạnh a. Tính bán kính mặt cầu ngoại tiếp hình nón theo a.

Cho hình chóp ta giác S.ABC có $\widehat{SAC}=\widehat{SBC}=90°$. Khi đó tâm mặt cầu ngoại tiếp hình chóp nằm trên đường thẳng nào?

Thể tích của khối cầu bán kính a bằng:

Cho hình nón có các kích thước r=1; h=2 với r. h lần lượt là bán kính đáy và độ dài đường cao hình nón. Diện tích toàn phần hình nón là:

Cho hình nón có bán kính đáy bằng 4a và chiều cao bằng 3a. Diện tích toàn phần của hình nón bằng

Số hình nón có được khi quay hình sau quanh trục BC là:

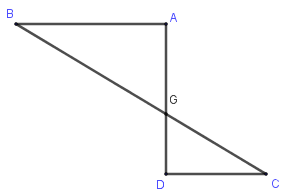
Nếu cắt mặt trụ tròn xoay bởi một mặt phẳng tạo với trục một góc $\alpha \left(0°<\alpha <90°\right)$thì ta được:

Cho khối (N) có bán kính đáy bằng 3 và diện tích xung quanh bằng $15\mathrm{\pi }$. Tính thể tích V của khối nón (N)

Cho một khối trụ có độ dài đường sinh l và bán kính đường tròn đáy là r. Diện tích toàn phần của hình trụ là:

Cho khối trụ có hai đáy là hình tròn (O;R) và (O';R), OO'=4R. Trên đường tròn tâm O lấy hai điểm A, B sao cho $AB=R\sqrt{3}$. Mặt phẳng (P) đi qua A, B cắt OO’ và tạo với đáy một góc bằng $60°$. (P) cắt khối trụ theo thiết diện là một phần của elip. Diện tích thiết diện đó bằng:

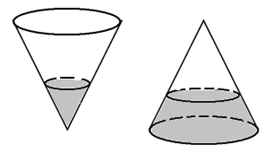
Một cái phễu có dạng hình nón có chiều cao 15 cm. Người ta đổ một lượng nước vào phễu sao cho chiều cao của lượng nước trong phễu bằng $\frac{1}{5}$chiều cao ban đầu của cái phễu (hình 1). Hỏi nếu bịt kín miệng phễu rồi lộn ngược phễu lên (hình 2) thì chiều cao của nước xấp xỉ bằng bao nhiêu (làm tròn đến hàng phần nghìn)

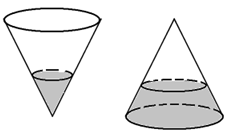
Một cái phễu có dạng hình nón. Chiều cao của phễu là 20 cm. người ta đổ một lượng nước vào phễu sao cho chiều cao của cột nước trong phễu bằng 10 cm. Nếu bịt kín miệng phễu rồi lật ngược phễu lên thì chiều cao của cột nước trong phễu gần bằng với giá trị nào sau đây?

Cho hình chóp S.ABCD có $\widehat{ABC}=\widehat{ADC}=90°$, cạnh bên SA vuông góc với (ABCD), góc tạo bởi SC và đáy ABCD bằng $60°$, CD = a và tam giác ADC có diện tích bằng $\frac{a^2\sqrt{3}}{2}$. Diện tích mặt cầu ngoại tiếp hình chóp S.ABCD là:

Cho hình nón $N_1$có chiều cao bằng 40 cm. gười ta cắt hình nón $N_1$bằng một mặt phẳng song song với đáy của nó để được một hình nón nhỏ $N_2$có thể tích bằng $\frac{1}{8}$thể tích $N_1$. Tính chiều cao h của hình nón $N_2$?

Cho hình chóp S.ABC có đáy là tam giác ABC đều, đường cao SH với H nằm trong tam giác ABC và 2SH=BC, (SBC) tạo với mặt phẳng (ABC) một góc $60°$. Biết có một điểm O nằm trên đường cao SH sao cho $d\left(O;AB\right)=d\left(O;AC\right)=d\left(O;\left(SBC\right)\right)=1$. Tính thể tích khối cầu ngoại tiếp hình chóp đã cho.

Cho hình trụ có chiều cao $h=a\sqrt{3}$, bán kính đáy r=a. Gọi O, O’ lần lượt là tâm của hai đường tròn đáy. Trên hai đường tròn đáy lần lượt lấy hai điểm A, B sao cho hai đường thẳng AB và OO’ chéo nhau và góc giữa hai đường thẳng AB với OO’ bằng $30°$. Khoảng cách giữa hai đường thẳng AB và OO’ bằng:

Hai quả bóng hình cầu có kích thước khác nhau được đặt ở hai góc của một căn nhà hình hộp chữ nhật sao cho mỗi quả bóng đều tiếp xúc với hai bức tường và nền của nhà đó. Biết rằng trên bề mặt của quả bóng đều tồn tại một điểm có khoảng cách đến hai bức tường và nền nhà mà nó tiếp xúc bằng 1, 2, 4. Tổng độ dài đường kính của hai quả bóng đó.

Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại A, $AB=a\sqrt{3}, BC=2a$, đường thẳng AC’ tạo với mặt phẳng (BCC’B’) một góc $30°$. Diện tích mặt cầu ngoại tiếp lăng trụ đã cho bằng:

Cho hình chóp tam giác đều S.ABC. Hình nón có đỉnh S và có đường tròn đáy là đường tròn tam giác ABC gọi là hình nón nội tiếp hình chóp S.ABC, hình nón có đỉnh S và có đường tròn đáy là đường tròn ngoại tiếp tam giác ABC gọi là hình nón ngoại tiếp hình chóp S.ABC. Tỉ số thể tích của hình nón nội tiếp và hình nón ngoại tiếp hình chóp đã cho là:

Cần đẽo thanh gỗ hình hộp có đáy là hình vuông thành hình trụ có cùng chiều cao. Tỉ lệ thể tích khối gỗ cần phải đẽo đi ít nhất (tính gần đúng) là:

Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông cân tại A, $AB=AC=a$và $AA\text{'}=a\sqrt{2}$. Thể tích khối cầu ngoại tiếp hình tứ diện AB’A’C là:

Một hộp đựng phấn hình hộp chữ nhật có chiều dài 30 cm, chiều rộng 5 cm và chiều cao 6 cm. Người ta xếp thẳng đứng vào đó các viên phấn giống nhau, mỗi viên phấn là khối trụ có chiều cao h = 6 cm và bán kính đáy $r=\frac{1}{2}$cm. Hỏi có thể xếp được tối đa bao nhiêu viên phấn.

Cho hình trụ có chiều cao bằng $6\sqrt{2}$cm. Biết rằng một mặt phẳng không vuông góc với đáy và cắt hai mặt đáy theo hai dây cung song song AB, CD mà AB=CD=6cm, diện tích tứ giác ABCD bằng $60c{m}^2$. Tính bán kính đáy của hình trụ.

Cho hình nón tròn xoay đỉnh S, đáy là hình tròn tâm O. Trên đường tròn đó lấy hai điểm A và M. Biết góc $\widehat{AOM}=60°$, góc tạo bởi hai mặt phẳng (SAM) và (OAM) có số đo bằng $30°$và khoảng cách từ O đến (SAM) bằng 2. Khi đó thể tích khối nón là:

Cho hình trụ (T) có (C),(C') là hai đường tròn đáy nội tiếp hai mặt đối diện của một hình lập phương. Biết rằng, trong tam giác cong tạo bởi đường tròn (C) và hình vuông ngoại tiếp của (C) có một hình chữ nhậ kích thước 1 x 2 (như hình vẽ dưới đây). Thể tích của khối trụ (T) là

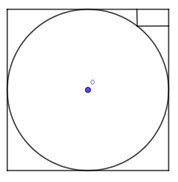
Cho tam giác nhọn ABC. Khi quay ABC quanh các cạnh BC, CA, AB ta được các hình tròn xoay có thể tích lần lượt là $\frac{3136\mathrm{\pi }}{5};\frac{9048\mathrm{\pi }}{13};672\mathrm{\pi }$. Tính diện tích tam giác ABC?

Cho tam giác ABC vuông cân tại A có AB=AC=12. Lấy một điểm M thuộc cạnh huyền BC và gọi H là hình chiếu của M lên cạnh góc vuông AB. Quay tam giác AMH quanh trục là đường thẳng AB tạo thành mặt nón tròn xoay (N), hỏi thể tích V của khối nón tròn xoay (N) lớn nhất là bao nhiêu?

Tứ diện ABCD có $AB=2,CD=2\sqrt{2}$ $\widehat{ABC}=\widehat{DAB}=90°$và góc giữa AD, BC bằng $45°$. Khi đó, bán kính mặt cầu ngoại tiếp tứ diện là:

Cho hình chóp S.ABC có SA vuông góc với đáy và $SA=a\sqrt{2}; \widehat{BAC}=45°$. Biết bán kính mặt cầu ngoại tiếp hình chóp S.ABC bằng a. Tính độ dài cạnh BC.