Cho hàm số
có bảng biến thiên như hình vẽ bên dưới.
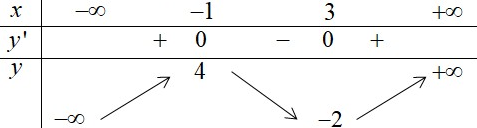
Số nghiệm thực phân biệt của phương trình
là
A.
.
B.
.
C.
.
D.
Đáp án đúng là: C
Cho hàm số
có bảng biến thiên như hình vẽ bên dưới.
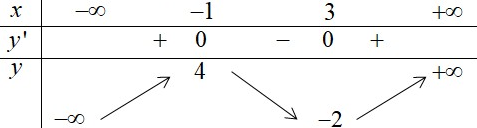
Số nghiệm thực phân biệt của phương trình là
.
.
.
Đáp án đúng là: C
Cho hàm số
có bảng biến thiên như hình vẽ bên dưới.
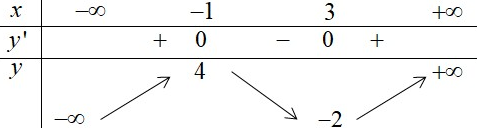
Số nghiệm thực phân biệt của phương trình là
A. . B. . C. . D.
Lời giải
Ta có:
Thì phương trình có nghiệm phân biệt.
với thì phương trình có nghiệm.
Vậy phương trình: có nghiệm thực phân biệt.
Câu hỏi tương tự:
#8447 THPT Quốc giaToán
Cho hàm số
có bảng biến thiên như hình vẽ bên. Khoảng cách giữa hai điểm cực trị của đồ thị hàm số đã cho bằng
Lượt xem: 143,767 Cập nhật lúc: 04:35 17/05/2025
#7566 THPT Quốc giaToán
Cho hàm số
có bảng biến thiên như hình vẽ bên
Có bao nhiêu giá trị nguyên của tham số để phương trình có nghiệm thực?
Lượt xem: 128,734 Cập nhật lúc: 04:29 17/05/2025
#7717 THPT Quốc giaToán
Cho hàm số
có bảng biến thiên như hình vẽ
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Lượt xem: 131,346 Cập nhật lúc: 05:40 14/05/2025
#7519 THPT Quốc giaToán
Cho hàm số
có bảng biến thiên như hình vẽ.
Giá trị cực tiểu của hàm số đã cho bằng
Lượt xem: 128,007 Cập nhật lúc: 07:43 17/05/2025
#8064 THPT Quốc giaToán
Cho hàm số
có bảng biến thiên như hình vẽ dưới đây. Hàm số có bao nhiêu điểm cực trị?
Lượt xem: 137,251 Cập nhật lúc: 07:44 17/05/2025
#8829 THPT Quốc giaToán
Cho hàm số có bảng biến thiên như hình vẽ sau:
Giá trị cực đại của hàm số đã cho bằng
Lượt xem: 150,178 Cập nhật lúc: 19:20 10/05/2025
#8332 THPT Quốc giaToán
Cho hàm số
có bảng biến thiên như hình vẽ. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Lượt xem: 141,794 Cập nhật lúc: 12:52 16/05/2025
#8182 THPT Quốc giaToán
Cho hàm số
có bảng biến thiên như hình vẽ. Hàm số đã cho đồng biến trên khoảng nào trong các khoảng dưới đây?
Lượt xem: 139,204 Cập nhật lúc: 18:18 14/05/2025
#8943 THPT Quốc giaToán
Cho hàm số
có bảng biến thiên như hình vẽ bên. Mệnh đề nào sau đây là sai?
Lượt xem: 152,275 Cập nhật lúc: 17:27 12/05/2025
Đề thi chứa câu hỏi này:
1 mã đề 50 câu hỏi 1 giờ 30 phút
418 xem21 thi
