Cho hình hộp đứng
có đáy
là hình thoi cạnh
,
. Gọi
là trọng tâm tam giác
, góc tạo bởi
với mặt phẳng đáy bằng
. Thể tích khối hộp
là
A.
.
B.
.
C.
.
D.
.
Đáp án đúng là: D
Cho hình hộp đứng có đáy là hình thoi cạnh , . Gọi là trọng tâm tam giác , góc tạo bởi với mặt phẳng đáy bằng . Thể tích khối hộp là
.
.
.
.
Đáp án đúng là: D
Cho hình hộp đứng
có đáy
là hình thoi cạnh
,
. Gọi
là trọng tâm tam giác
, góc tạo bởi
với mặt phẳng đáy bằng
. Thể tích khối hộp
là
A.
. B.
. C.
. D.
.
Lời giải
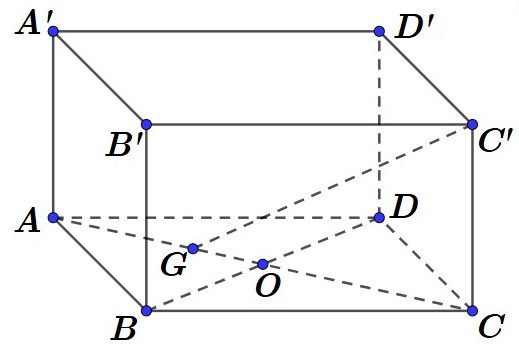
nên tam giác đều .
Ta có là trọng tâm tam giác nên .
Ta có là hình chiếu của trên nên là hình chiếu của trên
Nên .
Khi đó .
Câu hỏi tương tự:
#7785 THPT Quốc giaToán
Cho hình chóp có đáy là hình thang , , . Biết rằng và . Cạnh bên hợp với đáy một góc . Gọi là góc giữa hai mặt phẳng và . Khẳng định nào dưới đây đúng?
Lượt xem: 132,515 Cập nhật lúc: 22:01 25/04/2025
#3779 THPT Quốc giaVật lý
Trong thí nghiệm về giao thoa sóng ở mặt chất lỏng, hai nguồn kết hợp đặt tại và cách nhau , dao động cùng pha cùng tần số theo phương thẳng đứng, phát ra hai sóng lan truyền trên mặt chất lỏng với tốc độ . Ở mặt chất lỏng, và là hai điểm sao cho là hình thang cân có đáy dài và đường cao dài . Số điểm cực tiểu giao thoa trên đoạn thẳng là
Lượt xem: 64,422 Cập nhật lúc: 19:15 24/04/2025
#2500 THPT Quốc giaVật lý
Trong thí nghiệm về giao thoa sóng ở mặt chất lỏng, hai nguồn kết hợp đặt tại và cách nhau , dao động cùng pha, cùng tần số theo phương thẳng đứng, phát ra hai sóng lan truyền trên mặt chất lỏng với tốc độ . Ở mặt chất lỏng, và là hai điểm sao cho là hình thang cân có đáy dài và đường cao dài . Số điểm cực đại giao thoa trên đoạn thẳng là
Lượt xem: 42,600 Cập nhật lúc: 22:04 25/04/2025
#4809 THPT Quốc giaVật lý
Ở mặt nước có hai nguồn kết hợp đặt tại A và B, dao động cùng pha theo phương thẳng đứng, có bước sóng λ. Trên có 9 vị trí mà ở đó các phân tử nước dao động với biên độ cực đại. C và D là hai điểm ở mặt nước sao cho là hình vuông. M là một điểm thuộc cạnh và nằm trên vân cực đại giao thoa bậc nhất . Biết phần tử tại M dao động cùng pha với các nguồn. Độ dài đoạn gần giá trị nào nhất sau đây?
Lượt xem: 81,845 Cập nhật lúc: 23:53 25/04/2025
#3028 THPT Quốc giaVật lý
Ở mặt nước, hai nguồn sóng kết hợp đặt tại hai điểm và , dao động cùng pha theo phương thẳng đứng, phát ra hai sóng lan truyền có bước sóng . Hai điểm và ở mặt nước sao cho là hình vuông. Trên đoạn thẳng có 19 điểm cực đại giao thoa. Trên đoạn thẳng , gọi là điểm cực đại giao thoa gần nhất và là điểm cực đại giao thoa mà phần tử sóng tại và dao động cùng pha với nhau. Độ dài đoạn thẳng ngắn nhất gần với giá trị nào sau đây?
Lượt xem: 51,555 Cập nhật lúc: 05:38 26/04/2025
#11848 THPT Quốc giaSinh học
Ở đậu Hà Lan, alen A quy định thân cao trội hoàn toàn so với alen a quy định thân thấp; alen B quy định hoa đỏ trội hoàn toàn so với alen b quy định hoa trắng. Hai cặp gen này phân li độc lập. Biết rằng không xảy ra đột biến, chọn 3 cây thân cao, hoa đỏ P cho giao phấn ngẫu nhiên được F1 . Theo lí thuyết, có bao nhiêu phát biểu sau đây đúng?
I, F1 có thể có kiểu hình 100% cao đỏ.
II, Nếu ở F1 thấp trắng chiếm 1/144 thì có 1 cây P dị hợp kép.
III, Nếu 3 cây P có kiểu gen khác nhau thì F1 có tỉ lệ kiểu hình là 34:1:1.
IV, Nếu có 2 cây P dị hợp kép thì F1 có thể có tỉ lệ kiểu hình là 29:3:3:1.
Lượt xem: 201,545 Cập nhật lúc: 16:04 25/04/2025
#5423 THPT Quốc giaVật lý
Cho đoạn mạch AB như hình vẽ, cuộn cảm thuần có độ tự cảm , tụ điện có điện dung , hộp kín Y chỉ chứa các phần tử mắc nối tiếp. Đặt vào hai đầu AB điện áp xoay chiều thì điện áp hiệu dụng hai đầu đoạn mạch MN là và điện áp hai đầu đoạn mạch AN lệch pha so với điện áp hai đầu đoạn mạch MB. Biết và . Công suất tiêu thụ của đoạn mạch AB gần nhất với giá trị nào sau đây?
Lượt xem: 92,354 Cập nhật lúc: 21:57 24/04/2025
#11076 THPT Quốc giaSinh học
Ở một loài động vật, xét 2 cặp gen quy định hai cặp tính trạng, alen trội là trội hoàn toàn. Cho 2 cây đều dị hợp 2 cặp gen giao phấn với nhau, thu được F1 có 4% số cá thể đồng hợp lặn về 2 cặp gen. Biết rằng không xảy ra đột biến nhưng xảy ra hoán vị gen ở cả giới đực và giới cái với tần số như nhau. Theo lí thuyết, có bao nhiêu phát biểu sau đây đúng?
I. Nếu hai cây P có kiểu gen giống nhau thì tần số hoán vị là 40%.
II. Ở F1, loại kiểu hình có 2 tính trạng trội chiếm 54%.
III. Cho cây dị hợp về 2 cặp gen lai phân tích, có thể thu được đời con có số cá thể đồng hợp lặn chiếm 10%.
IV. F1 có 5 kiểu gen quy định kiểu hình trội về 2 tính trạng.
Lượt xem: 188,457 Cập nhật lúc: 12:49 25/04/2025
Đề thi chứa câu hỏi này:
1 mã đề 50 câu hỏi 1 giờ 30 phút
552 xem28 thi
