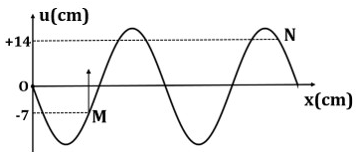
Một sóng ngang truyền trên sợi dây đủ dài với  bước sóng 60 cm. Khi chưa có sóng truyền qua, gọi M và N là hai điểm  gắn với hai phần tử trên dây cách nhau 85 cm. Hình bên là hình vẽ mô tả  hình dạng sợi dây khi có sóng truyền qua ở thời điểm t, trong đó điểm M  đang dao động về vị trí cân bằng. Coi biên độ sóng không đổi trong quá  trình truyền sóng. Gọi t + ∆t là thời điểm gần t nhất mà khoảng cách  giữa M và N đạt giá trị lớn nhất (với ∆t > 0). Diện tích hình thang tạo bởi M, N ở thời điểm t và M, N thời  điểm t + ∆t gần nhất với kết quả nào sau đây?

A.  

2230 cm².

B.  

2560 cm².

C.  

2165 cm².

D.  

2315 cm².

Đáp án đúng là: D

Hướng dẫn: Tại thời điểm t, điểm M đang đi lên → sóng truyền từ N tới M
→ Điểm N sớm pha hơn điểm M → điểm N đang đi xuống
Độ lệch pha giữa hai điểm M, N là: 
$\Delta \varphi = \dfrac{2 \pi d}{\lambda} = \dfrac{2 \pi . 85}{60} = \dfrac{17 \pi}{6} = 2 \pi + \dfrac{5 \pi}{6} \left( \text{rad} \right)$
Hai điểm M, N có khoảng cách lớn nhất khi chúng đối xứng qua trục Oy Ta có vòng tròn lượng giác: 

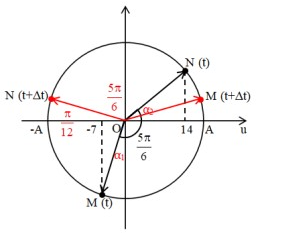
Từ vòng tròn lượng giác ta thấy: 
α₁ +α₂ = $\frac{5\pi }{6}-\frac{\pi }{2}=\frac{\pi }{3}$
$\Rightarrow arcsin \dfrac{7}{A} + arccos \dfrac{14}{A} = \dfrac{2 \pi}{3} \Rightarrow A \approx 17 , 35 \left(   \text{cm} \right)$
Ở thời điểm t + ∆t, hai điểm M, N đối xứng qua trục Oy, ta có:
$\left{ x_{2 N} = A cos \left(\right. \dfrac{\pi}{12} + \dfrac{5 \pi}{6} \right) \approx - 16 , 76 \left(   \text{cm} \right) \\ x_{2 M} = A cos \dfrac{\pi}{12} \approx 16 , 76 \left(   \text{cm} \right)$
Diện tích hình thang tạo bởi M, N ở thời điểm t và M, N thời điểm t + ∆t là:
$S = \dfrac{\left( \left|\right. x_{2 M} - x_{1 M} \left|\right. + \left|\right. x_{2 N} - x_{1 N} \left|\right. \right) \cdot d}{2} = \dfrac{\left( \left|\right. 16 , 76 - \left(\right. - 7 \right) \left| + \left|\right. - 16 , 76 - 14 \left|\right. \right) \cdot 85}{2} = 2317 , 1 \left(   \left(\text{cm}\right)^{2} \right)$
Diện tích S có giá trị gần nhất là 2315 cm2