Xét hàm số
với
là tham số thực. Gọi
là tập hợp tất cả các giá trị của
sao cho
\left{\right. f \left( x \right) + f \left( y \right) = 1 \\ e^{x + y} \leq e . \left( x + y \right) . Tìm tổng các phần tử của tập
.
A.
B.
C.
D.
Đáp án đúng là: B
Xét hàm số với là tham số thực. Gọi là tập hợp tất cả các giá trị của sao cho \left{\right. f \left( x \right) + f \left( y \right) = 1 \\ e^{x + y} \leq e . \left( x + y \right) . Tìm tổng các phần tử của tập .
Đáp án đúng là: B
Xét hàm số
với
là tham số thực. Gọi
là tập hợp tất cả các giá trị của
sao cho
Tìm tổng các phần tử của tập
.
A.
B.
C.
D.
Lời giải
Ta có:
.
Đặt
.
Có:
Xét
, có
.
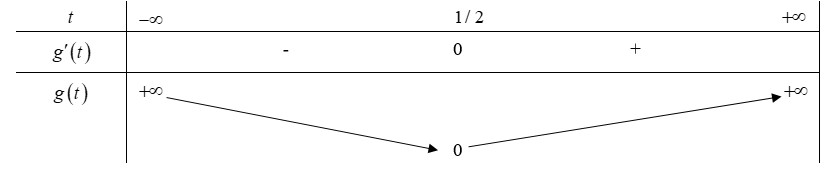
Từ bbt ta được .
Vậy (*) xảy ra
Vậy tổng các phần tử của tập S bằng 0.
Câu hỏi tương tự:
#8418 THPT Quốc giaToán
Cho hàm số
xác định với mọi
và có bảng xét dấu của
như sau:
Số điểm cực trị của hàm số là:
Lượt xem: 143,278 Cập nhật lúc: 06:09 11/05/2025
#8581 THPT Quốc giaToán
Xét hàm số liên tục trên đoạn và thoả mãn điều kiện Tích phân bằng
Lượt xem: 146,022 Cập nhật lúc: 07:38 11/05/2025
#8817 THPT Quốc giaToán
Cho hàm số bậc năm
và đồ thị hàm số
là đường cong trong hình vẽ dưới đây
Xét hàm số là tham số. Số giá trị nguyên của thuộc nửa khoảng để hàm số đồng biến trên khoảng là
Lượt xem: 150,113 Cập nhật lúc: 06:26 10/05/2025
#8045 THPT Quốc giaToán
Cho hàm số
xác định trên
và có bảng xét dấu:
Hàm số có bao nhiêu điểm cực trị?
Lượt xem: 136,874 Cập nhật lúc: 22:45 10/05/2025
#8782 THPT Quốc giaToán
Cho hàm số
có bảng xét dấu đạo hàm như sau
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Lượt xem: 149,454 Cập nhật lúc: 07:47 12/05/2025
#8658 THPT Quốc giaToán
Cho hàm số
có
có đạo hàm liên tục trên
và bảng xét dấu đạo hàm như sau
Hàm số có bao nhiêu điểm cực trị?
Lượt xem: 147,373 Cập nhật lúc: 09:18 12/05/2025
#8354 THPT Quốc giaToán
Cho hàm số
có bảng xét dấu của đạo hàm như sau:
Hàm số đã cho nghịch biến trên khoảng
Lượt xem: 142,205 Cập nhật lúc: 14:10 11/05/2025
#11161 THPT Quốc giaToán
Cho hàm số
có bảng xét dấu của đạo hàm
như sau:
Giá trị cực tiểu của hàm số bằng
Lượt xem: 190,199 Cập nhật lúc: 14:19 11/05/2025
#7671 THPT Quốc giaToán
Cho hàm số
có bảng xét dấu của đạo hàm như sau
Số điểm cực trị của hàm số đã cho là
Lượt xem: 130,574 Cập nhật lúc: 14:14 11/05/2025
Đề thi chứa câu hỏi này:
1 mã đề 50 câu hỏi 1 giờ 30 phút
552 xem23 thi
