Một con lắc lò xo dao động điều hòa theo phương ngang với tần số góc ω. Vật nhỏ của con lắc có khối lượng 100g. Tại thời điểm t = 0, vật nhỏ qua vị trí cân bằng theo chiều dương. Tại thời điểm t = 0,95s, vận tốc v và li độ x của vật nhỏ thỏa mãn v= - ωx lần thứ 5. Độ cứng của lò xo là
A. 85N/m.B. 37N/m.C. 20N/m.D. 25N/m. Đáp án đúng là: D
Một con lắc lò xo dao động điều hòa theo phương ngang với tần số góc ω. Vật nhỏ của con lắc có khối lượng 100g. Tại thời điểm t = 0, vật nhỏ qua vị trí cân bằng theo chiều dương. Tại thời điểm t = 0,95s, vận tốc v và li độ x của vật nhỏ thỏa mãn v= - ωx lần thứ 5. Độ cứng của lò xo là
Đáp án đúng là: D
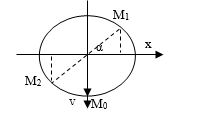
Ta có phương trình dao động của vật là:
Vận tốc v= - ωx ứng với trường hợp vật hướng về vị trí cân bằng
Khi t = 0,95s:
Thời điểm đầu tiên vật qua v= - ωxở M1:
Mỗi chu kì vật qua v= - ωx hai lần, do đó lần thứ 5:
Câu hỏi tương tự:
#63 THPT Quốc giaVật lý
Một con lắc lò xo dao động điều hoà theo phương thẳng đứng, đồ thị phụ thuộc thời gian của lực đàn hồi được biểu diễn như hình vẽ. Biết biên độ dao động của vật bằng , lấy , . Động năng của vật biến thiên với tần số là
Lượt xem: 1,234 Cập nhật lúc: 04:21 16/05/2025
#2978 THPT Quốc giaVật lý
Một con lắc lò xo dao động điều hòa theo phương thẳng đứng ở nơi có gia tốc rơi tự do . Tại vị trí cân bằng, lò xo dãn . Chu kì dao động của con lắc là
Lượt xem: 50,794 Cập nhật lúc: 05:23 15/05/2025
#5879 THPT Quốc giaVật lý
Một con lắc lò xo dao động điều hòa theo phương trình . Khi pha dao động là rad thì vận tốc chất điểm có giá trị . Khi qua vị trí li độ thì độ lớn vận tốc có giá trị là
Lượt xem: 100,095 Cập nhật lúc: 08:33 13/05/2025
#7487 THPT Quốc giaVật lý
Một con lắc lò xo dao động điều hòa theo phương thẳng đứng. Khi vật nặng của con lắc ở vị trí thấp nhất thì lò xo bị dãn , còn khi vật nặng của con lắc ờ vị trí cao nhất thì lò xo bị nén . Tỉ số của biên độ dao động của vật so với độ dãn của lò xo ở vị trí cân bằng là
Lượt xem: 127,440 Cập nhật lúc: 06:24 15/05/2025
#1149 THPT Quốc giaVật lý
Một con lắc lò xo dao động điều hòa theo phương thẳng đứng, khi con lắc ở vị trí cân bằng lò xo dãn , thời gian con lắc bị nén trong 1 chu kì là . Lấy . Biên độ dao động của vật là:
Lượt xem: 19,688 Cập nhật lúc: 20:40 13/05/2025
#4545 THPT Quốc giaVật lý
Một con lắc lò xo dao động điều hòa theo phương ngang, dọc theo trục . Gốc tọa độ O trùng vị trí cân bằng của vật, ở vị trí cân bằng lò xo không biến dạng. Biết trong mỗi chu kỳ dao động, khoảng thời gian mà lò xo bị giãn đồng thời véc tơ vận tốc và véc tơ gia tốc ngược chiều là . Chu kỳ dao động điều hòa của con lắc bằng
Lượt xem: 77,455 Cập nhật lúc: 20:34 14/05/2025
#4075 THPT Quốc giaVật lý
Một con lắc lò xo dao động điều hòa theo phương ngang với biên độ . Nếu chọn mốc thế năng tại vị trí cân bằng thì khi qua vị trí cân bằng con lắc có động năng . Tại vị trí biên, lực đàn hồi lò xo có độ lớn
Lượt xem: 69,424 Cập nhật lúc: 05:08 11/05/2025
#7457 THPT Quốc giaVật lý
Một con lắc lò xo dao động điều hòa theo phương thẳng đứng với khối lượng . Từ vị trí cân bằng kéo xuống rồi buông nhẹ. Biết chiều dài tự nhiên của lò xo là . Trong quá trình dao động chiều dài lớn nhất và nhỏ nhất của lò xo là
Lượt xem: 126,933 Cập nhật lúc: 19:51 16/05/2025
#2117 THPT Quốc giaVật lý
Một con lắc lò xo dao động điều hoà theo phương thẳng đứng. Trong quá trình dao động của vật, chiều dài của lò xo thay đổi từ 20cm đến 28cm. Biên độ dao động của vật là
Lượt xem: 36,065 Cập nhật lúc: 14:23 14/05/2025
Đề thi chứa câu hỏi này:
1 mã đề 40 câu hỏi 50 phút
122,531 xem9,418 thi
