Trang chủ Đề thi THPT Quốc gia Toán 12297
thumbnail

(2025 Mới) Đề Thi Ôn Tập THPT Môn Toán Có Đáp Án - Đề Số 2

<p>Cùng luyện tập với đề thi ôn tập THPT môn Toán năm 2025 (Đề số 2), kèm đáp án chi tiết, giúp học sinh củng cố kiến thức và nâng cao kỹ năng giải bài. Đề thi được thiết kế theo cấu trúc chuẩn của Bộ GD&amp;ĐT, bao gồm các câu hỏi trọng tâm trong chương trình Toán 12, hỗ trợ ôn luyện hiệu quả cho kỳ thi tốt nghiệp THPT quốc gia 2025. Đặc biệt, đáp án chi tiết sẽ giúp bạn hiểu rõ cách giải và nâng cao khả năng làm bài.</p><h3>&nbsp;</h3>

Từ khoá: đề thi ôn tập môn Toán 2025 có đáp ánđề thi Toán THPT 2025đề thi ôn thi Toán đề số 2đề thi Toán 2025 kèm đáp ánluyện thi môn Toán THPT 2025đề thi Toán THPT 2025tài liệu ôn thi Toán 2025 có đáp ánđề thi thử môn Toán THPT quốc gia 2025luyện thi Toán 2025 có đáp ánđề thi Toán THPT số 2

Đề thi nằm trong bộ sưu tập: 📘 Tuyển Tập Đề Thi Tham Khảo Các Môn THPT Quốc Gia 2025 🎯📘 Tuyển Tập Bộ 500 Đề Thi Ôn Luyện Môn Toán THPT Quốc Gia Các Tỉnh Từ Năm 2018-2025 - Có Đáp Án Chi Tiết

Số câu hỏi: 22 câuSố mã đề: 1 đềThời gian: 1 giờ

159,957 lượt xem 12,297 lượt làm bài


Bạn chưa làm đề thi này!!!

 

Xem trước nội dung:

Câu 1: 0.25 điểm
Trong không gian với hệ toạ độ Oxyz, phương trình nào sau đây là phương trình tham số của đường thẳng?
A.  

{x=1+2ty=−3+4tz=5−7t\left\{ \begin{array}{l} x = 1 + 2t \\ y = -3 + 4t \\ z = 5 - 7t \end{array} \right.

B.  

{x=3+t2y=2+9tz=−6+11t\left\{ \begin{array}{l} x = 3 + t^2 \\ y = 2 + 9t \\ z = -6 + 11t \end{array} \right.

C.  

{x=9+17ty=8+2tz=−12+t\left\{ \begin{array}{l} x = 9 + 17t \\ y = 8 + 2t \\ z = -12 + t \end{array} \right.

D.  

{x=15+ty=25+tz=35−t\left\{ \begin{array}{l} x = 15 + t \\ y = 25 + t \\ z = 35 - t \end{array} \right.

Câu 2: 0.25 điểm

Cho hình hộp ABCD⋅A′B′C′D′.ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }. Cặp vectơ nào sau đây là cặp vectơ chỉ phương của mặt phẳng (ABCD)({\rm{ABCD}}) ?

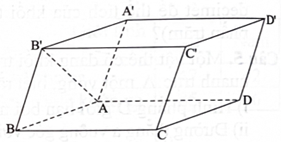
Hình ảnh
A.  
AB→,AA→.\overrightarrow {{\rm{AB}}} ,\overrightarrow {{\rm{AA}}} .
B.  
AB→,AB′→\overrightarrow {{\rm{AB}}} ,\overrightarrow {{\rm{A}}{{\rm{B}}^\prime }}
C.  
AB→,A′B→.\overrightarrow {{\rm{AB}}} ,\overrightarrow {{{\rm{A}}^\prime }{\rm{B}}} .
D.  
AD→,A′B′→.\overrightarrow {{\rm{AD}}} ,\overrightarrow {{{\rm{A}}^\prime }{{\rm{B}}^\prime }} .
Câu 3: 0.25 điểm

Cho hàm số f(x){\rm{f}}({\rm{x}}) có đồ thị như hình bên. Biết rằng một trong bốn đường thẳng sau đây là đường tiệm cận xiên của đồ thị hàm số, đường đó là đường nào?

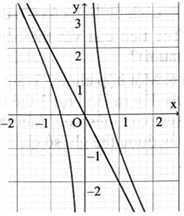
Hình ảnh
A.  
y=2x.y = 2x.
B.  
y=−x2.{\rm{y}} = \frac{{ - {\rm{x}}}}{2}.
C.  
y=−2x.y = - 2x.
D.  
y=x2.{\rm{y}} = \frac{{\rm{x}}}{2}.
Câu 4: 0.25 điểm

Cho hàm số f(x){\rm{f}}({\rm{x}}) có đồ thị như hình bên. Biết rằng một trong bốn điểm sau đây là tâm đối xứng của đồ thị hàm số, điểm đó là điểm nào?

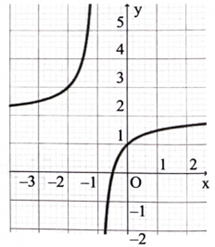
Hình ảnh
A.  
M(0;1).{\rm{M}}(0;1).
B.  
N(−1;2).{\rm{N}}( - 1;2).
C.  
P(−2;3).{\rm{P}}( - 2;3).
D.  
Q(0;3).{\rm{Q}}(0;3).
Câu 5: 0.25 điểm
Phát biểu nào sau đây là đúng với f(x){\rm{f}}({\rm{x}}) là hàm số bất kì liên tục trên R\mathbb{R} ?
A.  
∫02f(x)dx=∫10f(x)dx+∫12f(x)dx.\int_0^2 f (x)dx = \int_1^0 f (x)dx + \int_1^2 f (x)dx.
B.  
∫02f(x)dx=∫01f(x)dx+∫21f(x)dx.\int_0^2 f (x)dx = \int_0^1 f (x)dx + \int_2^1 f (x)dx.
C.  
∫02f(x)dx=∫10f(x)dx+∫21f(x)dx.\int_0^2 f (x)dx = \int_1^0 f (x)dx + \int_2^1 f (x)dx.
D.  
∫02f(x)dx=∫01f(x)dx+∫12f(x)dx.\int_0^2 f (x)dx = \int_0^1 f (x)dx + \int_1^2 f (x)dx.
Câu 6: 0.25 điểm
Trong không gian với hệ tọa độ Oxyz, khoảng cách từ điểm M(9;7;8){\rm{M}}(9;7;8) đến mặt phẳng (P):ax+by+cz+d=0({\rm{P}}):{\rm{ax}} + {\rm{by}} + {\rm{cz}} + {\rm{d}} = 0 bằng
A.  
∣7a+8  b+9c+d∣a2+b2+c2.\frac{{|7{\rm{a}} + 8\;{\rm{b}} + 9{\rm{c}} + {\rm{d}}|}}{{\sqrt {{{\rm{a}}^2} + {{\rm{b}}^2} + {{\rm{c}}^2}} }}.
B.  
∣9a+7  b+8c+d∣a2+b2+c2.\frac{{|9{\rm{a}} + 7\;{\rm{b}} + 8{\rm{c}} + {\rm{d}}|}}{{\sqrt {{{\rm{a}}^2} + {{\rm{b}}^2} + {{\rm{c}}^2}} }}.
C.  
∣7a+8  b+9c+d∣72+82+92.\frac{{|7{\rm{a}} + 8\;{\rm{b}} + 9{\rm{c}} + {\rm{d}}|}}{{\sqrt {{7^2} + {8^2} + {9^2}} }}.
D.  
∣9a+7b+8c+d∣92+72+82.\frac{{|9a + 7b + 8c + d|}}{{\sqrt {{9^2} + {7^2} + {8^2}} }}.
Câu 7: 0.25 điểm
Trong không gian với hệ toạ độ Oxyz, vectơ nào sau đây là một vectơ pháp tuyến của mặt y−2x−5z+8=0.{\rm{y}} - 2{\rm{x}} - 5{\rm{z}} + 8 = 0.
A.  
n1→=(1;2;5).\overrightarrow {{n_1}} = (1;2;5).
B.  
n2→=(1;−2;−5).\overrightarrow {{{\rm{n}}_2}} = (1; - 2; - 5).
C.  
n3→=(−2;1;−5).\overrightarrow {{n_3}} = ( - 2;1; - 5).
D.  
n4→=(2;1;5).\overrightarrow {{{\rm{n}}_4}} = (2;1;5).
Câu 8: 0.25 điểm
Trong không gian với hệ tọa độ Oxyz mặt cầu (x+13)2+(y−14)2+(z−15)2=42{({\rm{x}} + 13)^2} + {({\rm{y}} - 14)^2} + {({\rm{z}} - 15)^2} = {4^2} có bán kính bằng
A.  
16.
B.  
2.
C.  
256.
D.  
4.
Câu 9: 0.25 điểm
Hàm số nào sau đây là một nguyên hàm của hàm số f(x)=1sin⁡2x{\rm{f}}({\rm{x}}) = \frac{1}{{{{\sin }^2}{\rm{x}}}} ?
A.  
F1(x)=tan⁡x+C.{F_1}(x) = \tan x + C.
B.  
F2(x)=−tan⁡x+C.{F_2}(x) = - \tan x + C.
C.  
F3(x)=−cot⁡x.{F_3}(x) = - \cot x.
D.  
F4(x)=cot⁡x.{{\rm{F}}_4}({\rm{x}}) = \cot {\rm{x}}.
Câu 10: 0.25 điểm
Trong mặt phẳng với hệ tọa độ Oxy, nếu hàm số y=f(x){\rm{y}} = {\rm{f}}({\rm{x}}) liên tục và nhận giá trị dương trên đoạn [1; 2] thì diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f(x){\rm{y}} = {\rm{f}}({\rm{x}}) và các đường thẳng y=0,x=1,x=2{\rm{y}} = 0,{\rm{x}} = 1,{\rm{x}} = 2 bằng
A.  
∫21∣f(x)∣dx.\int_2^1 | f(x)|dx.
B.  
∫12f(x)dx.\int_1^2 f (x)dx.
C.  
π∫12(f(x))2dx.\pi \int_1^2 {({\rm{f}}(} {\rm{x}}){)^2}{\rm{dx}}.
D.  
π∫21(f(x))2dx.\pi \int_2^1 {({\rm{f}}(} {\rm{x}}){)^2}{\rm{dx}}.
Câu 11: 0.25 điểm
Nếu các biến cố A,B{\rm{A}},{\rm{B}} thoả mãn P(A)>0,P(B)>0{\rm{P}}({\rm{A}}) > 0,{\rm{P}}({\rm{B}}) > 0 thì biểu thức P(B∣A){\rm{P}}({\rm{B}}\mid {\rm{A}}) bằng
A.  
P(A∣B)⋅P(B)P(A).\frac{{{\rm{P}}({\rm{A}}\mid {\rm{B}}) \cdot {\rm{P}}({\rm{B}})}}{{{\rm{P}}({\rm{A}})}}.
B.  
P(A∣B)⋅P(A)P(B).\frac{{{\rm{P}}({\rm{A}}\mid {\rm{B}}) \cdot {\rm{P}}({\rm{A}})}}{{{\rm{P}}({\rm{B}})}}.
C.  
P(A∣B)P(B).\frac{{{\rm{P}}({\rm{A}}\mid {\rm{B}})}}{{{\rm{P}}({\rm{B}})}}.
D.  
P(A∣B)P(A).\frac{{{\rm{P}}({\rm{A}}\mid {\rm{B}})}}{{{\rm{P}}({\rm{A}})}}.
Câu 12: 0.25 điểm
Nếu một mẫu số liệu có phương sai bằng 0,09 thì có độ lệch chuẩn bằng
A.  
0,09.
B.  
0,045.
C.  
0,3.
D.  
0,0081.
Câu 13: 1 điểmchọn đúng/sai

Trong mỗi ý a), b), c), d) ở mỗi câu, thi sinh chọn đúng hoặc sai.

Cho hàm số f(x)=ax3+bx2+cx+d(a,b,c{\rm{f}}({\rm{x}}) = {\rm{a}}{{\rm{x}}^3} + {\rm{b}}{{\rm{x}}^2} + {\rm{cx}} + {\rm{d}}({\rm{a}},{\rm{b}},{\rm{c}} , d∈R{\rm{d}} \in \mathbb{R} ) có đồ thị như hình bên.

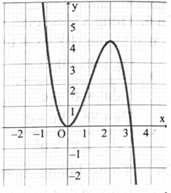
Hình ảnh
A.
 
Điểm cực tiểu của hàm số là 0.
B.
 
Điểm cực đại của hàm số là 4.
C.
 
Hàm số đồng biến trên khoảng (0; 3).
D.
 
Giá trị lớn nhất của hàm số trên đoạn [-1; 3] bằng 4.
Câu 14: 1 điểmchọn đúng/sai

Trong mỗi ý a), b), c), d) ở mỗi câu, thi sinh chọn đúng hoặc sai.

Trong không gian với hệ toạ độ Oxyz, cho đường hai đường thẳng Δ 1 : x = 1 y = 2 − 3 t 1 z = − t 1 và Δ 2 : x = − 1 y = 2 + t 2 z = 3 + 3 t 2

A.
 
Đường thẳng Δ1\Delta_1 có một vectơ chỉ phương với tọa độ là (0;−3;−1)(0; -\sqrt{3}; -1).
B.
 
Đường thẳng Δ2\Delta_2 có một vectơ chỉ phương với tọa độ là (0;−1;3)(0; -1; \sqrt{3}).
C.
 
Tích độ dài của hai vectơ u→(0;−3;−1)\overrightarrow{u}(0; -\sqrt{3}; -1) và v→(0;1;3)\overrightarrow{v}(0; 1; \sqrt{3}) bằng 4.
D.
 
Góc giữa hai đường thẳng Δ1\Delta_1 và Δ2\Delta_2 là 60∘60^\circ.
Câu 15: 1 điểmchọn đúng/sai

Trong mỗi ý a), b), c), d) ở mỗi câu, thi sinh chọn đúng hoặc sai.

Một phương tiện giao thông đang chuyển động thẳng đều với vận tốc a(m/s){\rm{a}}({\rm{m}}/{\rm{s}}) thì người điều khiển phương tiện đạp phanh. Từ thời điểm đó, phương tiện chuyển động chậm dần đều với vận tốc thay đổi theo hàm số v = -4t + 12 (m/s), trong đó tt là thời gian tính bằng giây kể từ lúc đạp phanh.

A.
 
Khi xe dừng hẳn thì vận tốc bằng 0 (m/s)0 \, (m/s).
B.
 
Thời gian từ lúc người lái xe đạp phanh cho đến khi dừng hẳn là 4 s4 \, s.
C.
 
∫(−4t+12)dt=−4t2+12t+C\int (-4t + 12)dt = -4t^2 + 12t + C.
D.
 
Quãng đường từ lúc đạp phanh cho đến khi dừng hẳn là 18 m18 \, m.
Câu 16: 1 điểmchọn đúng/sai
Trong mỗi ý a), b), c), d) ở mỗi câu, thi sinh chọn đúng hoặc sai.

Một hộp có 4 viên bi xanh và 6 viên bi đỏ, các viên bi có kích thước và khối lượng như nhau. Lấy lần lượt hai viên bi, không hoàn lại.

A.
 
Xác suất lần 1 lấy được bi xanh là 14\frac{1}{4}.
B.
 
Xác suất lần 2 lấy được bi xanh biết lần 1 lấy được bi đỏ là 13\frac{1}{3}.
C.
 
Xác suất lần 2 lấy được bi xanh biết lần 1 lấy được bi xanh là 49\frac{4}{9}.
D.
 
Xác suất lần 2 lấy được bi xanh là 25\frac{2}{5}.
Câu 17: 0.5 điểm

Nền nhà tầng một của một hội trường có độ cao 1 m so với mặt đất. Từ nền nhà tầng 1 lên nền nhà tầng 2 có một cầu thang 21 bậc, độ cao của các bậc so với mặt đất theo thứ tự lập thành một cấp số cộng (un)\left( {{u_n}} \right) có 21 số hạng: u1=1,  d=0,16{{\rm{u}}_1} = 1,\;{\rm{d}} = 0,16 (đơn vị là mét). Độ cao của bậc thứ 8 so với mặt đất là bao nhiêu mét?

Câu 18: 0.5 điểm

Bất phương trình log⁡12x>−3{\log _{\frac{1}{2}}}{\rm{x}} > - 3 có tất cả bao nhiêu nghiệm là số nguyên?

Câu 19: 0.5 điểm

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): x2+y2+z2−8x+{x^2} + {y^2} + {z^2} - 8x + 16y+21z−100=0.16{\rm{y}} + 21{\rm{z}} - 100 = 0. Giả sử I(a;b;c){\rm{I}}({\rm{a}};{\rm{b}};{\rm{c}}) là tâm của (S).({\rm{S}}). Giá trị của biểu thức M =a−2  b+c = {\rm{a}} - 2\;{\rm{b}} + {\rm{c}} là bao nhiêu?

Câu 20: 0.5 điểm

Khi sản xuất vỏ lon đồ hộp hình trụ có thể tích là V=128π(cm3){\rm{V}} = 128\pi \left( {{\rm{c}}{{\rm{m}}^3}} \right) , các nhà thiết kế luôn đặt mục tiêu sao cho chi phí nguyên liệu làm vỏ lon là ít nhất, tức là diện tích toàn phần của hình trụ là nhỏ nhất. Muốn thể tích khối trụ đó bằng V=128π(cm3){\rm{V}} = 128\pi \left( {{\rm{c}}{{\rm{m}}^3}} \right) và diện tích toàn phần hình trụ nhỏ nhất thì bán kính đáy bằng bao nhiêu cm ?

Câu 21: 0.5 điểm

Hoạ sĩ thiết kế một micro có dạng khối tròn xoay, mặt cắt đứng chứa trục của khối tròn xoay có dạng như hình sau, trong đó OA=OB=OI=2  cm{\rm{OA}} = {\rm{OB}} = {\rm{OI}} = 2\;{\rm{cm}} , MC=MD=1  cm{\rm{MC}} = {\rm{MD}} = 1\;{\rm{cm}} , đường thẳng OM là đường trung trực của đoạn thẳng CD, OM=20  cm,AOB^=90o.{\rm{OM}} = 20\;{\rm{cm}},\widehat {{\rm{AOB}}} = {90^o }. Thể tích của micro này là bao nhiêu cm3{\rm{c}}{{\rm{m}}^3} ? (Làm tròn kết quả đến hàng đơn vị)

Hình ảnh
Câu 22: 0.5 điểm

E-mail Filter là một phần mềm chặn email quảng cáo. Nếu một email là thư quảng cáo, phần mềm sẽ chuyển nó vào thư mục Spam với xác suất là 0,9. Ngược lại, nếu một email không là thư quảng cáo, phần mềm có thể chuyển nó vào thư mục Spam với xác suất 0,05. Thống kê trong một số lượng lớn email bị chuyển vào thư mục Spam thì thấy tỉ lệ thư quảng cáo là 72%. Xác suất một email là thư quảng cáo là bao nhiêu? (Làm tròn kết quả đến hàng phần trăm)

Đề thi tương tự

(2025 Mới) Đề Thi Ôn Tập THPT Môn Toán Có Đáp Án - Đề Số 4

1 mã đề 22 câu hỏi 1 giờ

173,597 xem13,344 thi

(2025 Mới) Đề Thi Ôn Tập THPT Môn Toán Có Đáp Án - Đề Số 5

1 mã đề 22 câu hỏi 1 giờ

173,957 xem13,374 thi

Đề Thi Ôn Tập THPT Mới 2025 Môn Toán Có Đáp Án - Đề Số 1

1 mã đề 22 câu hỏi 1 giờ

186,383 xem14,329 thi

Đề Thi Ôn Tập THPT Mới 2025 Môn Toán Có Đáp Án - Đề Số 3

1 mã đề 22 câu hỏi 1 giờ

178,601 xem13,728 thi

(2025 mới) Đề ôn thi tốt nghiệp THPT Ngữ văn (Đề số 22)

1 mã đề 7 câu hỏi 1 giờ

306,187 xem23,543 thi

(2025 mới) Đề ôn thi tốt nghiệp THPT môn Văn có đáp án (Đề số 55)

1 mã đề 7 câu hỏi 1 giờ

292,398 xem22,487 thi

(2025 Mới) Đề Ôn Thi Tốt Nghiệp THPT Tiếng Anh Có Đáp Án Miễn Phí (Đề Số 8)

1 mã đề 40 câu hỏi 1 giờ

241,389 xem18,565 thi

(2025 Mới) Đề Ôn Thi Tốt Nghiệp THPT Tiếng Anh Có Đáp Án Miễn Phí (Đề Số 9)

1 mã đề 40 câu hỏi 1 giờ

273,330 xem21,020 thi

(2025 mới) Đề ôn thi tốt nghiệp THPT môn Văn có đáp án (Đề số 46)

1 mã đề 7 câu hỏi 1 giờ

224,482 xem17,255 thi