Trang chủ Đề thi THPT Quốc gia Toán 13344
thumbnail

(2025 Mới) Đề Thi Ôn Tập THPT Môn Toán Có Đáp Án - Đề Số 4

<p>Cùng luyện tập với đề thi ôn tập THPT môn Toán năm 2025 (Đề số 4), kèm đáp án chi tiết, giúp học sinh củng cố kiến thức vững vàng và nâng cao kỹ năng giải bài. Đề thi được biên soạn sát với cấu trúc đề thi của Bộ GD&amp;ĐT, bao gồm các câu hỏi quan trọng từ chương trình Toán 12. Đặc biệt, đáp án chi tiết giúp học sinh hiểu rõ phương pháp giải, rèn luyện kỹ năng làm bài và chuẩn bị tốt nhất cho kỳ thi tốt nghiệp THPT quốc gia 2025.</p><h3>&nbsp;</h3>

Từ khoá: đề thi ôn tập môn Toán 2025 có đáp ánđề thi Toán THPT 2025đề thi ôn thi Toán đề số 4đề thi Toán 2025 kèm đáp ánluyện thi môn Toán THPT 2025đề thi Toán THPT 2025tài liệu ôn thi Toán 2025 có đáp ánđề thi thử môn Toán THPT quốc gia 2025luyện thi Toán 2025 có đáp ánđề thi Toán THPT số 4

Đề thi nằm trong bộ sưu tập: 📘 Tuyển Tập Đề Thi Tham Khảo Các Môn THPT Quốc Gia 2025 🎯📘 Tuyển Tập Bộ 500 Đề Thi Ôn Luyện Môn Toán THPT Quốc Gia Các Tỉnh Từ Năm 2018-2025 - Có Đáp Án Chi Tiết

Số câu hỏi: 22 câuSố mã đề: 1 đềThời gian: 1 giờ

173,594 lượt xem 13,344 lượt làm bài


Bạn chưa làm đề thi này!!!

 

Xem trước nội dung:

Câu 1: 0.25 điểm

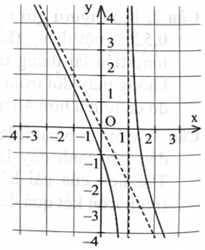
Đồ thị hàm số y=ax2+bx+cmx+n(a,b,c,m,n∈R){\rm{y}} = \frac{{{\rm{a}}{{\rm{x}}^2} + {\rm{bx}} + {\rm{c}}}}{{{\rm{mx}} + {\rm{n}}}}({\rm{a}},{\rm{b}},{\rm{c}},{\rm{m}},{\rm{n}} \in \mathbb{R}) ở hình bên có đường tiệm cận xiên là một trong bốn đường thẳng dưới đây, đường thẳng đó là đường nào?

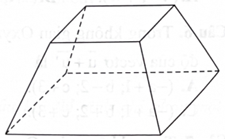
Hình ảnh
A.  
y=2x.{\rm{y}} = 2{\rm{x}}.
B.  
x=1.{\rm{x}} = 1.
C.  
y=−2x.{\rm{y}} = - 2{\rm{x}}.
D.  
y=−3x.y = - 3x.
Câu 2: 0.25 điểm
Nếu một khối chóp có diện tích mặt đáy bằng S và có chiều cao bằng h thì có thể tích bằng
A.  
Sh3.\frac{{{\rm{Sh}}}}{3}.
B.  
Sh.
C.  
3 Sh.
D.  
πSh3.\frac{{\pi {\rm{Sh}}}}{3}.
Câu 3: 0.25 điểm
Tất cả các nghiệm của phương trình cos⁡x=−22\cos x = \frac{{ - \sqrt 2 }}{2} là
A.  
x=3π4+kπ,x=−3π4+kπ,∀k∈Z.x = \frac{{3\pi }}{4} + {\rm{k}}\pi ,{\rm{x}} = \frac{{ - 3\pi }}{4} + {\rm{k}}\pi ,\forall {\rm{k}} \in \mathbb{Z}.
B.  
x=3π4+kπ2,x=−3π4+kπ2,∀k∈Z.{\rm{x}} = \frac{{3\pi }}{4} + {\rm{k}}\frac{\pi }{2},{\rm{x}} = \frac{{ - 3\pi }}{4} + {\rm{k}}\frac{\pi }{2},\forall {\rm{k}} \in \mathbb{Z}.
C.  
x=3π4+k2π,x=−3π4+k2π,∀k∈Z.{\rm{x}} = \frac{{3\pi }}{4} + {\rm{k}}2\pi ,{\rm{x}} = \frac{{ - 3\pi }}{4} + {\rm{k}}2\pi ,\forall {\rm{k}} \in \mathbb{Z}.
D.  
x=3π4+k3π,x=−3π4+k3π,∀k∈Z.{\rm{x}} = \frac{{3\pi }}{4} + {\rm{k}}3\pi ,{\rm{x}} = \frac{{ - 3\pi }}{4} + {\rm{k}}3\pi ,\forall {\rm{k}} \in \mathbb{Z}.
Câu 4: 0.25 điểm
Nếu cấp số nhân (un)\left( {{u_n}} \right) có số hạng đầu u1=3{u_1} = 3 và công bội q=3q = 3 thì số hạng un{u_n} bằng
A.  
3n.{3^{\rm{n}}}.
B.  
3n−1.{3^{{\rm{n}} - 1}}.
C.  
3n+1.{3^{{\rm{n}} + 1}}.
D.  
3+(n−1)⋅3.3 + ({\rm{n}} - 1) \cdot 3.
Câu 5: 0.25 điểm
Tập nghiệm của bất phương trình log⁡0,5x>4{\log _{0,5}}x > 4 là
A.  
(40,5;+∞).\left( {{4^{0,5}}; + \infty } \right).
B.  
(−∞;40,5).\left( { - \infty ;{4^{0,5}}} \right).
C.  
(0;2).(0;2).
D.  
(0;(0,5)4).\left( {0;{{(0,5)}^4}} \right).
Câu 6: 0.25 điểm
Trong không gian Oxyz, cho hai vectơ u→=(−a;b;c),u→′=(1;−2;3).\overrightarrow {\rm{u}} = ( - {\rm{a}};{\rm{b}};{\rm{c}}),{\overrightarrow {\rm{u}} ^\prime } = (1; - 2;3). Toạ độ của vectơ u→+u′→\overrightarrow {\rm{u}} + \overrightarrow {{u^\prime }} là
A.  
(−a+1;b−2;c+3).( - {\rm{a}} + 1;{\rm{b}} - 2;{\rm{c}} + 3).
B.  
(a+1;b−2;c+3).({\rm{a}} + 1;{\rm{b}} - 2;{\rm{c}} + 3).
C.  
(−a+1;b+2;c+3).( - {\rm{a}} + 1;{\rm{b}} + 2;{\rm{c}} + 3).
D.  
(a+1;b+2;c+3).(a + 1;b + 2;{\rm{c}} + 3).
Câu 7: 0.25 điểm
Trong không gian Oxyz, tọa độ của vectơ u→=2j→−3k→\overrightarrow {\rm{u}} = 2\overrightarrow {\rm{j}} - 3\overrightarrow {\rm{k}} là
A.  
(0;−2;−3).(0; - 2; - 3).
B.  
(0;−2;3).(0; - 2;3).
C.  
(0;2;−3).(0;2; - 3).
D.  
(0;2;3).(0;2;3).
Câu 8: 0.25 điểm
Phát biểu nào sau đây là đúng về mối quan hệ của các đường thẳng trong không gian?
A.  
Nếu hai đường thẳng a,b{\rm{a}},{\rm{b}} phân biệt và cùng vuông góc với đường thẳng c thì hai đường thẳng a và b song song với nhau.
B.  
Nếu hai đường thẳng a,b{\rm{a}},{\rm{b}} phân biệt và cùng vuông góc với đường thẳng c thì hai đường thẳng a và b vuông góc với nhau.
C.  
Nếu hai đường thẳng a,b{\rm{a}},{\rm{b}} phân biệt và cùng vuông góc với đường thẳng c thì hai đường thẳng a và b không có điểm chung
D.  
Nếu hai đường thẳng a,b{\rm{a}},{\rm{b}} cắt nhau và cùng vuông góc với đường thẳng c thì đường thẳng c vuông góc với mặt phẳng chứa a và b.
Câu 9: 0.25 điểm
Nếu hàm số y=f(x){\rm{y}} = {\rm{f}}({\rm{x}}) liên tục và nhận giá trị dương trên tập số thực thì diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f(x){\rm{y}} = {\rm{f}}({\rm{x}}) , trục Ox và các đường thẳng x=7;x=9{\rm{x}} = 7;{\rm{x}} = 9 bằng
A.  
∫97∣f(x)∣dx.\int_9^7 | f(x)|dx.
B.  
∫79f(x)dx.\int_7^9 f (x)dx.
C.  
π∫79(f(x))2dx.\pi \int_7^9 {({\rm{f}}(} {\rm{x}}){)^2}{\rm{dx}}.
D.  
π∫97(f(x))2dx.\pi \int_9^7 {({\rm{f}}(} {\rm{x}}){)^2}{\rm{dx}}.
Câu 10: 0.25 điểm
Nếu các biến cố A,B{\rm{A}},{\rm{B}} thoả mãn P(A∩B)=0,2;P(B)=0,5{\rm{P}}({\rm{A}} \cap {\rm{B}}) = 0,2;{\rm{P}}({\rm{B}}) = 0,5 thì
A.  
P(A∣B)=0,3.{\rm{P}}({\rm{A}}\mid {\rm{B}}) = 0,3.
B.  
P(A∣B)=0,7.{\rm{P}}({\rm{A}}\mid {\rm{B}}) = 0,7.
C.  
P(A∣B)=0,01.{\rm{P}}({\rm{A}}\mid {\rm{B}}) = 0,01.
D.  
P(A∣B)=0,4.{\rm{P}}({\rm{A}}\mid {\rm{B}}) = 0,4.
Câu 11: 0.25 điểm
Phát biểu nào sau đây là đúng?
A.  
∫11−2xdx=ln⁡(1−2x)+C.\int {\frac{1}{{1 - 2{\rm{x}}}}} {\rm{dx}} = \ln (1 - 2{\rm{x}}) + C.
B.  
∫11−2xdx=ln⁡∣1−2x∣+C.\int {\frac{1}{{1 - 2{\rm{x}}}}} {\rm{dx}} = \ln |1 - 2{\rm{x}}| + C.
C.  
∫11−2xdx=12ln⁡∣1−2x∣+C.\int {\frac{1}{{1 - 2{\rm{x}}}}} {\rm{dx}} = \frac{1}{2}\ln |1 - 2{\rm{x}}| + C.
D.  
∫11−2xdx=−12ln⁡∣1−2x∣+C.\int {\frac{1}{{1 - 2{\rm{x}}}}} {\rm{dx}} = \frac{{ - 1}}{2}\ln |1 - 2{\rm{x}}| + C.
Câu 12: 0.25 điểm
Cho hình chóp S.ABCD{\rm{S}}.{\rm{ABCD}} có tất cả các cạnh bằng nhau. Số đo góc giữa hai đường thẳng SA và CD bằng
A.  
60o.{60^o }.
B.  
30o.{30^o }.
C.  
45o.{45^o }.
D.  
90o.{90^o }.
Câu 13: 1 điểmchọn đúng/sai
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Một khối bê tông có dạng hình chóp cụt tứ giác đều với cạnh đáy lớn là 6 dm, cạnh đáy nhỏ là 4 dm, khoảng cách giữa hai mặt phẳng chứa đáy bằng 4 dm (hình bên).

Hình ảnh
A.
 
Diện tích của đáy nhỏ là 16 dm216 \, \text{dm}^2.
B.
 
Diện tích của đáy lớn là 24 dm224 \, \text{dm}^2.
C.
 
Chiều cao của khối bê tông là 4 cm4 \, \text{cm}.
D.
 
Thể tích của khối bê tông (làm tròn đến hàng đơn vị của dm3\text{dm}^3) là 101 dm3101 \, \text{dm}^3.
Câu 14: 1 điểmchọn đúng/sai
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng

Δ:x+11=y+52=z+93,Δ′:x+63=y+32=z1\Delta :\frac{{{\rm{x}} + 1}}{1} = \frac{{{\rm{y}} + 5}}{2} = \frac{{{\rm{z}} + 9}}{3},{\Delta ^\prime }:\frac{{{\rm{x}} + 6}}{3} = \frac{{{\rm{y}} + 3}}{2} = \frac{{\rm{z}}}{1}

A.
 
Hai vectơ u→(1;2;3)\overrightarrow{u}(1; 2; 3), u′→(3;2;1)\overrightarrow{u'}(3; 2; 1) lần lượt là vectơ chỉ phương của Δ,Δ′\Delta, \Delta'.
B.
 
Điểm M(−1;−5;−9)M(-1; -5; -9) không thuộc đường thẳng Δ\Delta, điểm M′(−6;−3;0)M'(-6; -3; 0) không thuộc đường thẳng Δ′\Delta'.
C.
 
[u→,u′→]=(−4;8;−4)[\overrightarrow{u}, \overrightarrow{u'}] = (-4; 8; -4).
D.
 
Hai đường thẳng Δ,Δ′\Delta, \Delta' chéo nhau.
Câu 15: 1 điểmchọn đúng/sai
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Cho a<5<b{\rm{a}} < 5 < {\rm{b}} và I=∫ab∣x−5∣dx.{\rm{I}} = \int_{\rm{a}}^{\rm{b}} | {\rm{x}} - 5|{\rm{dx}}.

A.
 
I=−∫a5∣x−5∣dx+∫5b∣x−5∣dxI = -\int_a^5 |x-5|dx + \int_5^b |x-5|dx.
B.
 
∫a5∣x−5∣dx=∫a5(5−x)dx=(5x−x22)∣a5=252−(5a−a22)\int_a^5 |x-5|dx = \int_a^5 (5-x)dx = \left(5x - \frac{x^2}{2}\right)\Big|_a^5 = \frac{25}{2} - \left(5a - \frac{a^2}{2}\right).
C.
 
∫5b∣x−5∣dx=∫5b(x−5)dx=(x22−5x)∣5b=(b22−5b)+252\int_5^b |x-5|dx = \int_5^b (x-5)dx = \left(\frac{x^2}{2} - 5x\right)\Big|_5^b = \left(\frac{b^2}{2} - 5b\right) + \frac{25}{2}.
D.
 
I=a2+b22−5a−5b+50I = \frac{a^2 + b^2}{2} - 5a - 5b + 50.
Câu 16: 1 điểmchọn đúng/sai
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Cho các biến cố A,B{\rm{A}},{\rm{B}} thoả mãn P(A∩B)=15;P(A∩B‾)=310;P(B)=25.{\rm{P}}({\rm{A}} \cap {\rm{B}}) = \frac{1}{5};{\rm{P}}({\rm{A}} \cap \overline {\rm{B}} ) = \frac{3}{{10}};{\rm{P}}({\rm{B}}) = \frac{2}{5}.

A.
 
P(B)=35\text{P(B)} = \frac{3}{5}.
B.
 
P(A | B)=13\text{P(A | B)} = \frac{1}{3}.
C.
 
P(A | B)=12\text{P(A | B)} = \frac{1}{2}.
D.
 
P(A)=12\text{P(A)} = \frac{1}{2}.
Câu 17: 0.5 điểm

Bảng dưới đây biểu diễn mẫu số liệu ghép nhóm về cân nặng của một số quả bưởi da xanh ở một khu vực (đơn vị: kg).

Nhóm

[1,2 ; 1,3)

[1,3 ; 1,4)

[1,4 ; 1,5)

[1,5 ; 1,6)

[1,6 ; 1,7)

Tần số

8

21

8

7

6

Số trung bình của mẫu số liệu ghép nhóm trên là bao nhiêu? (Làm tròn kết quả đến hàng phần trăm)

Câu 18: 0.5 điểm

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): x2+y2+z2−2x−4y+6z−67=0.{x^2} + {y^2} + {z^2} - 2x - 4{\rm{y}} + 6{\rm{z}} - 67 = 0. Bán kính của mặt cầu bằng bao nhiêu?

Câu 19: 0.5 điểm

 

Trong không gian với hệ tọa độ Oxyz, góc giữa đường thẳng Δ:{x=0y=tz=−3t\Delta : \left\{ \begin{array}{l} x = 0 \\ y = t \\ z = -\sqrt{3}t \end{array} \right.và mặt phẳng (P):3y−z−1=0(P): \sqrt{3}y - z - 1 = 0là n∘n^\circvới nn là số thực. Giá trị của nn là bao nhiêu?

 

Câu 20: 0.5 điểm

Một vật chuyển động theo quy luật s(t)=6t2−t3s(t) = 6{t^2} - {t^3} với tt (giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và s (mét) là quãng đường vật đi được trong thời gian đó. Trong khoảng 6 giây kể từ lúc vật bắt đầu chuyển động, vận tốc lớn nhất của vật là xm/s.{\rm{xm}}/{\rm{s}}. Giá trị của x là bao nhiêu?

Câu 21: 0.5 điểm

Nhân ngày khai trương siêu thị MC, các khách hàng vào siêu thị được đánh số thứ tự là các số tự nhiên liên tiếp và có thể được tặng quà (khách hàng đầu tiên được đánh số thứ tự là số 1 ). Cứ 4 khách vào MC thì khách thứ tư được tặng một cái lược chải tóc, cứ 5 khách vào MC thì khách thứ năm được tặng một cái khăn mặt, cứ 6 khách vào MC thì khách thứ sáu được tặng một hộp kem đánh răng. Sau 30 phút mở cửa, có 200 khách đầu tiên vào MC và tất cả khách vẫn ở trong MC. Chọn ngẫu nhiên một khách trong 200 khách đầu tiên, xác suất để chọn được khách hàng được tặng cả ba món quà bằng ab\frac{{\rm{a}}}{{\rm{b}}} với a,b{\rm{a}},{\rm{b}} là các số nguyên dương và b<400.{\rm{b}} < 400. Giá trị của a−b{\rm{a}} - {\rm{b}} là bao nhiêu?

Câu 22: 0.5 điểm

Hai bạn Việt và Nam mỗi người thực hiện một thí nghiệm một cách độc lập với nhau. Xác suất thực hiện thành công thí nghiệm của Việt và Nam lẩn lượt là 0,6 và 0,7. Xác suất có đúng một trong hai người thực hiện thành công thí nghiệm biết rằng có ít nhất một người thực hiện thành công thí nghiệm là ab\frac{{\rm{a}}}{{\rm{b}}} với a,b∈N,b<50.{\rm{a}},{\rm{b}} \in \mathbb{N},{\rm{b}} < 50. Giá trị của a+b{\rm{a}} + {\rm{b}} là bao nhiêu?

Đề thi tương tự

(2025 Mới) Đề Thi Ôn Tập THPT Môn Toán Có Đáp Án - Đề Số 2

1 mã đề 22 câu hỏi 1 giờ

159,957 xem12,297 thi

(2025 Mới) Đề Thi Ôn Tập THPT Môn Toán Có Đáp Án - Đề Số 5

1 mã đề 22 câu hỏi 1 giờ

173,957 xem13,374 thi

Đề Thi Ôn Tập THPT Mới 2025 Môn Toán Có Đáp Án - Đề Số 1

1 mã đề 22 câu hỏi 1 giờ

186,381 xem14,329 thi

Đề Thi Ôn Tập THPT Mới 2025 Môn Toán Có Đáp Án - Đề Số 3

1 mã đề 22 câu hỏi 1 giờ

178,598 xem13,728 thi

(2025 mới) Đề ôn thi tốt nghiệp THPT Ngữ văn (Đề số 22)

1 mã đề 7 câu hỏi 1 giờ

306,184 xem23,543 thi

(2025 mới) Đề ôn thi tốt nghiệp THPT môn Văn có đáp án (Đề số 55)

1 mã đề 7 câu hỏi 1 giờ

292,398 xem22,487 thi

(2025 Mới) Đề Ôn Thi Tốt Nghiệp THPT Tiếng Anh Có Đáp Án Miễn Phí (Đề Số 8)

1 mã đề 40 câu hỏi 1 giờ

241,389 xem18,565 thi

(2025 Mới) Đề Ôn Thi Tốt Nghiệp THPT Tiếng Anh Có Đáp Án Miễn Phí (Đề Số 9)

1 mã đề 40 câu hỏi 1 giờ

273,329 xem21,020 thi

(2025 mới) Đề ôn thi tốt nghiệp THPT môn Văn có đáp án (Đề số 46)

1 mã đề 7 câu hỏi 1 giờ

224,480 xem17,255 thi